Previous in Matrices and Determinants Next in Matrices and Determinants
Question Number 54741 by gunawan last updated on 10/Feb/19
$$\mathrm{such}\:\mathrm{that} \\ $$$$\mathrm{1}.\begin{pmatrix}{\mathrm{n}}\\{\mathrm{0}}\end{pmatrix}^{\mathrm{2}} +\begin{pmatrix}{\mathrm{n}}\\{\mathrm{1}}\end{pmatrix}^{\mathrm{2}} +...+\begin{pmatrix}{\mathrm{n}}\\{\mathrm{n}}\end{pmatrix}^{\mathrm{2}} =\frac{\left(\mathrm{2}{n}\right)!}{\left({n}!\right)^{\mathrm{2}} } \\ $$$$\mathrm{2}.\:\begin{pmatrix}{\mathrm{n}}\\{\mathrm{0}}\end{pmatrix}+\frac{\mathrm{1}}{\mathrm{2}}\begin{pmatrix}{\mathrm{n}}\\{\mathrm{1}}\end{pmatrix}+...+\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\begin{pmatrix}{\mathrm{n}}\\{\mathrm{n}}\end{pmatrix}^{\mathrm{2}} =\frac{\mathrm{2}^{{n}+\mathrm{1}} −\mathrm{1}}{{n}+\mathrm{1}} \\ $$
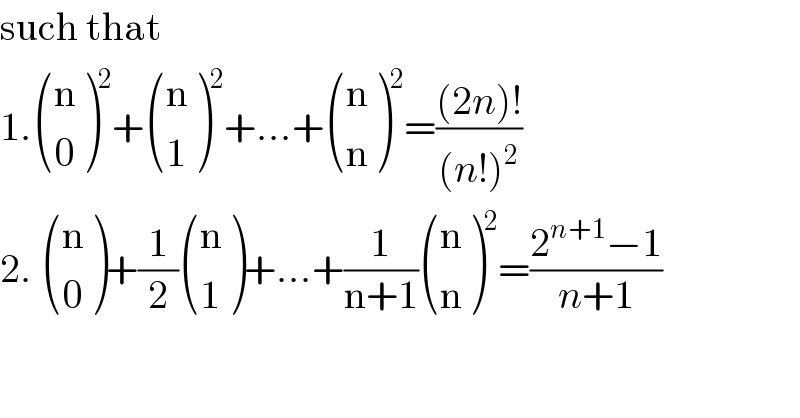
Commented by Abdo msup. last updated on 10/Feb/19
$$\left.\mathrm{1}\right)\:{we}\:{have}\:\left(\mathrm{1}+{x}\right)^{\mathrm{2}{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{\mathrm{2}{n}} ^{{k}} \:{x}^{{k}} \:\:{and} \\ $$$$\left(\mathrm{1}+{x}\right)^{\mathrm{2}{n}} =\left(\mathrm{1}+{x}\right)^{{n}} \left(\mathrm{1}+{x}\right)^{{n}} =\left(\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} {x}^{{k}} \right)\left(\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:{x}^{{k}} \right) \\ $$$$=\sum_{{k}=\mathrm{0}} ^{\mathrm{2}{n}} \:{c}_{{k}} \:{x}^{\mathrm{2}{k}} \:\:\:{with}\:{c}_{{k}} =\sum_{{i}+{j}\:={k}} \:{a}_{{i}} {b}_{{j}} \\ $$$$=\sum_{{i}=\mathrm{0}} ^{{k}} \:{a}_{{i}} {b}_{{k}−{i}} \:=\sum_{{i}=\mathrm{0}} ^{{k}} \:{C}_{{n}} ^{{i}} \:{C}_{{n}} ^{{k}−{i}} \:=\sum_{{i}=\mathrm{0}} ^{{k}} \left({C}_{{n}} ^{{i}} \right)^{\mathrm{2}} \:\Rightarrow \\ $$$${c}_{{n}} =\sum_{{i}=\mathrm{0}} ^{{n}} \left(\:{C}_{{n}} ^{{i}} \right)^{\mathrm{2}} \:\:{but}\:{c}_{{n}} \:{is}\:{the}\:{coefficient}\:{of}\:{x}^{\mathrm{2}{n}} \:\:{in}\:{the} \\ $$$${expantion}\:{of}\:\left(\mathrm{1}+{x}\right)^{\mathrm{2}{n}} \:\Rightarrow{c}_{{n}} ={C}_{\mathrm{2}{n}} ^{{n}} \:=\frac{\left(\mathrm{2}{n}\right)!}{\left({n}!\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\left({C}_{{n}} ^{\mathrm{0}} \right)^{\mathrm{2}} \:+\left({C}_{{n}} ^{\mathrm{1}} \right)^{\mathrm{2}} \:+\left({C}_{{n}} ^{\mathrm{3}} \right)^{\mathrm{2}} \:+...+\left({C}_{{n}} ^{{n}} \right)^{\mathrm{2}} \:=\frac{\left(\mathrm{2}{n}\right)!}{\left({n}!\right)^{\mathrm{2}} }\:. \\ $$
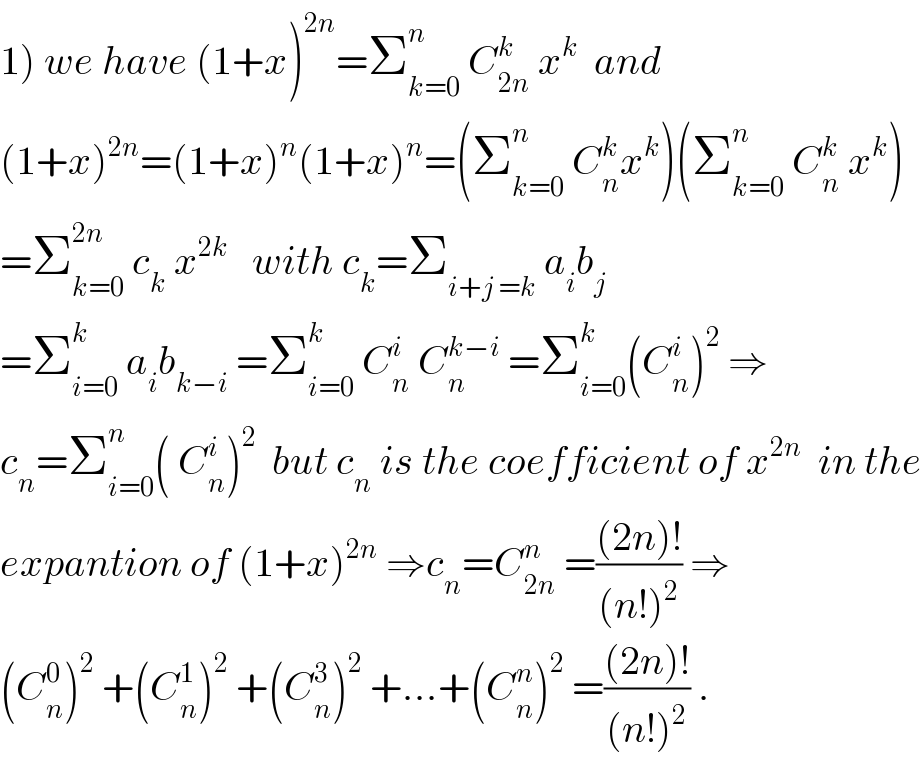
Answered by tanmay.chaudhury50@gmail.com last updated on 10/Feb/19
![1)(1+x)^n =nc_0 +nc_1 x+nc_2 x^2 +...+nc_n x^n (1+(1/x))^n =nc_0 +nc_1 ×(1/x)+nc_2 ×(1/x^2 )+..+nc_n ×(1/x^n ) multiply right hand side and take x independent terms.. (nc_0 )^2 +(nc_1 )^2 +(nc_2 )^2 +...+(nc_n )^2 multiply left hand side and take the coefficient of xindepent terms (1+x)^n ×(1+(1/x))^n =(1+x)^n ×(1+x)^n ×(1/x^n ) =x^(−n) (1+x)^(2n) let( r+1)th term of (1+x)^(2n) contains x^n t_(r+1) =2nc_r (x)^r hence x^r =x^n r=n t_(n+1) =2nc_n (x)^n contains x^n x^(−n) ×2nc_n x^n =2nc_n →x independendent... (nc_0 )^2 +(nc_1 )^2 +..(nc_n )^2 =2nc_n =(((2n)!)/(n!×n!)) 2)∫_0 ^1 (1+x)^n dx=∫_0 ^1 [nc_0 +nc_1 x+nc_2 x^2 +...+nc_n x^n ]dx ∣(((1+x)^(n+1) )/(n+1))∣_0 ^1 =∣nc_0 x+(1/2)nc_1 x^2 +(1/3)nc_2 x^3 +..+(1/(n+1))nc_n x^(n+1) ∣_0 ^1 ((2^(n+1) −1)/(n+1))=nc_0 +(1/2)nc_1 +(1/3)nc_2 +...+(1/(n+1))nc_n](Q54753.png)
$$\left.\mathrm{1}\right)\left(\mathrm{1}+{x}\right)^{{n}} ={nc}_{\mathrm{0}} +{nc}_{\mathrm{1}} {x}+{nc}_{\mathrm{2}} {x}^{\mathrm{2}} +...+{nc}_{{n}} {x}^{{n}} \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{{n}} ={nc}_{\mathrm{0}} +{nc}_{\mathrm{1}} ×\frac{\mathrm{1}}{{x}}+{nc}_{\mathrm{2}} ×\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+..+{nc}_{{n}} ×\frac{\mathrm{1}}{{x}^{{n}} } \\ $$$${multiply}\:\:{right}\:{hand}\:{side}\:{and}\:{take}\:{x}\:{independent} \\ $$$${terms}.. \\ $$$$\left({nc}_{\mathrm{0}} \right)^{\mathrm{2}} +\left({nc}_{\mathrm{1}} \right)^{\mathrm{2}} +\left({nc}_{\mathrm{2}} \right)^{\mathrm{2}} +...+\left({nc}_{{n}} \right)^{\mathrm{2}} \\ $$$${multiply}\:{left}\:{hand}\:{side}\:{and}\:{take}\:{the}\:{coefficient} \\ $$$${of}\:{xindepent}\:{terms} \\ $$$$\left(\mathrm{1}+{x}\right)^{{n}} ×\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{{n}} \\ $$$$=\left(\mathrm{1}+{x}\right)^{{n}} ×\left(\mathrm{1}+{x}\right)^{{n}} ×\frac{\mathrm{1}}{{x}^{{n}} } \\ $$$$={x}^{−{n}} \left(\mathrm{1}+{x}\right)^{\mathrm{2}{n}} \\ $$$${let}\left(\:{r}+\mathrm{1}\right){th}\:{term}\:{of}\:\left(\mathrm{1}+{x}\right)^{\mathrm{2}{n}} {contains}\:{x}^{{n}} \\ $$$${t}_{{r}+\mathrm{1}} =\mathrm{2}{nc}_{{r}} \left({x}\right)^{{r}} \\ $$$${hence}\:{x}^{{r}} ={x}^{{n}} \\ $$$${r}={n}\:\:\: \\ $$$${t}_{{n}+\mathrm{1}} =\mathrm{2}{nc}_{{n}} \left({x}\right)^{{n}} \:{contains}\:{x}^{{n}} \\ $$$$\boldsymbol{{x}}^{−\boldsymbol{{n}}} ×\mathrm{2}\boldsymbol{{nc}}_{\boldsymbol{{n}}} \boldsymbol{{x}}^{\boldsymbol{{n}}} \\ $$$$=\mathrm{2}\boldsymbol{{nc}}_{\boldsymbol{{n}}} \rightarrow{x}\:{independendent}... \\ $$$$\left({nc}_{\mathrm{0}} \right)^{\mathrm{2}} +\left({nc}_{\mathrm{1}} \right)^{\mathrm{2}} +..\left({nc}_{{n}} \right)^{\mathrm{2}} =\mathrm{2}{nc}_{{n}} =\frac{\left(\mathrm{2}{n}\right)!}{{n}!×{n}!} \\ $$$$ \\ $$$$\left.\mathrm{2}\right)\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+{x}\right)^{{n}} {dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \left[{nc}_{\mathrm{0}} +{nc}_{\mathrm{1}} {x}+{nc}_{\mathrm{2}} {x}^{\mathrm{2}} +...+{nc}_{{n}} {x}^{{n}} \right]{dx} \\ $$$$\mid\frac{\left(\mathrm{1}+{x}\right)^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\mid_{\mathrm{0}} ^{\mathrm{1}} =\mid{nc}_{\mathrm{0}} {x}+\frac{\mathrm{1}}{\mathrm{2}}{nc}_{\mathrm{1}} {x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{3}}{nc}_{\mathrm{2}} {x}^{\mathrm{3}} +..+\frac{\mathrm{1}}{{n}+\mathrm{1}}{nc}_{{n}} {x}^{{n}+\mathrm{1}} \mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\frac{\mathrm{2}^{{n}+\mathrm{1}} −\mathrm{1}}{{n}+\mathrm{1}}={nc}_{\mathrm{0}} +\frac{\mathrm{1}}{\mathrm{2}}{nc}_{\mathrm{1}} +\frac{\mathrm{1}}{\mathrm{3}}{nc}_{\mathrm{2}} +...+\frac{\mathrm{1}}{{n}+\mathrm{1}}{nc}_{{n}} \\ $$
Commented by gunawan last updated on 10/Feb/19
$$\mathrm{wow}\:\mathrm{thank}\:{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir} \\ $$$$ \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 10/Feb/19
$${most}\:{welcome}... \\ $$