Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 54790 by Anju last updated on 11/Feb/19

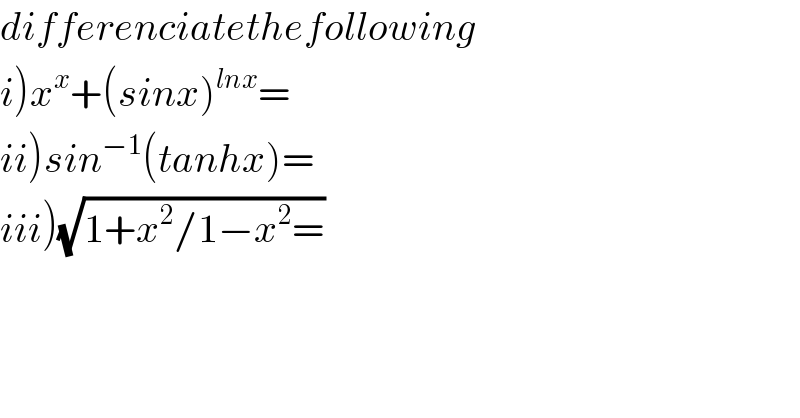
differenciatethefollowing i)x^x +(sinx)^(lnx) = ii)sin^(−1) (tanhx)= iii)(√(1+x^2 /1−x^2 =))

$${differenciatethefollowing} \\ $$$$\left.{i}\right){x}^{{x}} +\left({sinx}\right)^{{lnx}} = \\ $$$$\left.{ii}\right){sin}^{−\mathrm{1}} \left({tanhx}\right)= \\ $$$$\left.{iii}\right)\sqrt{\mathrm{1}+{x}^{\mathrm{2}} /\mathrm{1}−{x}^{\mathrm{2}} =} \\ $$

Commented by maxmathsup by imad last updated on 11/Feb/19

1) let f(x)=x^x +(sinx)^(ln(x)) ⇒f(x)=e^(xln(x)) + e^(ln(x)ln(sinx)) with x>0 ⇒ f^′ (x) =(xlnx)^′ x^x +(lnx ln(sinx))^′ (sinx)^(ln(x)) =(lnx +1) x^x +(((ln(sinx))/x) +lnx ((cosx)/(sinx)))(sinx)^(ln(x)) =(1+ln(x))x^x + (((ln(sinx))/x) +lnx cotan(x))(sinx)^(ln(x)) .

$$\left.\mathrm{1}\right)\:{let}\:{f}\left({x}\right)={x}^{{x}} \:+\left({sinx}\right)^{{ln}\left({x}\right)} \:\Rightarrow{f}\left({x}\right)={e}^{{xln}\left({x}\right)} \:+\:{e}^{{ln}\left({x}\right){ln}\left({sinx}\right)} \:\:\:\:{with}\:{x}>\mathrm{0}\:\Rightarrow \\ $$$${f}^{'} \left({x}\right)\:=\left({xlnx}\right)^{'} \:{x}^{{x}} \:\:+\left({lnx}\:{ln}\left({sinx}\right)\right)^{'} \:\left({sinx}\right)^{{ln}\left({x}\right)} \\ $$$$=\left({lnx}\:+\mathrm{1}\right)\:{x}^{{x}} \:+\left(\frac{{ln}\left({sinx}\right)}{{x}}\:+{lnx}\:\frac{{cosx}}{{sinx}}\right)\left({sinx}\right)^{{ln}\left({x}\right)} \\ $$$$=\left(\mathrm{1}+{ln}\left({x}\right)\right){x}^{{x}} \:+\:\left(\frac{{ln}\left({sinx}\right)}{{x}}\:+{lnx}\:{cotan}\left({x}\right)\right)\left({sinx}\right)^{{ln}\left({x}\right)} \:. \\ $$

Commented by maxmathsup by imad last updated on 11/Feb/19

ii) let g(x)=arcsin(tanhx) we have tanhx =((sh(x))/(ch(x))) =((e^x −e^(−x) )/(e^x +e^(−x) )) =((e^(2x) −1)/(e^(2x) +1)) ⇒ g(x)=arcsin(((e^(2x) −1)/(e^(2x) +1))) ⇒g^′ (x)=(((((e^(2x) −1)/(e^(2x) +1)))^′ )/(√(1−(((e^(2x) −1)/(e^(2x) +1)))^2 ))) but (((e^(2x) −1)/(e^(2x) +1)))^′ =((2e^(2x) (e^(2x) +1) −2e^(2x) (e^(2x) −1))/((e^(2x) +1)^2 )) =((4 e^(2x) )/((e^(2x) +1)^2 )) ⇒ g^′ (x) = ((4 e^(2x) )/((e^(2x) +1)^2 ((√((e^(2x) +1)^2 −(e^(2x) −1)^2 ))/(e^(2x) +1)))) =((4 e^(2x) )/((e^(2x) +1)(√(e^(4x) +2e^(2x) +1−e^(4x) +2e^(2x) −1)))) =((4 e^(2x) )/((1+e^(2x) )2e^x )) =((2e^x )/((1+ e^(2x) ))) ⇒g^′ (x) =((2e^x )/((1+e^(2x) ))) .

$$\left.{ii}\right)\:{let}\:{g}\left({x}\right)={arcsin}\left({tanhx}\right)\:\:{we}\:{have}\:{tanhx}\:=\frac{{sh}\left({x}\right)}{{ch}\left({x}\right)}\:=\frac{{e}^{{x}} −{e}^{−{x}} }{{e}^{{x}} \:+{e}^{−{x}} }\:=\frac{{e}^{\mathrm{2}{x}} −\mathrm{1}}{{e}^{\mathrm{2}{x}} \:+\mathrm{1}}\:\Rightarrow \\ $$$${g}\left({x}\right)={arcsin}\left(\frac{{e}^{\mathrm{2}{x}} −\mathrm{1}}{{e}^{\mathrm{2}{x}} \:+\mathrm{1}}\right)\:\Rightarrow{g}^{'} \left({x}\right)=\frac{\left(\frac{{e}^{\mathrm{2}{x}} −\mathrm{1}}{{e}^{\mathrm{2}{x}} \:+\mathrm{1}}\right)^{'} }{\sqrt{\mathrm{1}−\left(\frac{{e}^{\mathrm{2}{x}} −\mathrm{1}}{{e}^{\mathrm{2}{x}} \:+\mathrm{1}}\right)^{\mathrm{2}} }}\:\:{but} \\ $$$$\left(\frac{{e}^{\mathrm{2}{x}} −\mathrm{1}}{{e}^{\mathrm{2}{x}} \:+\mathrm{1}}\right)^{'} \:=\frac{\mathrm{2}{e}^{\mathrm{2}{x}} \left({e}^{\mathrm{2}{x}} \:+\mathrm{1}\right)\:−\mathrm{2}{e}^{\mathrm{2}{x}} \left({e}^{\mathrm{2}{x}} −\mathrm{1}\right)}{\left({e}^{\mathrm{2}{x}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\mathrm{4}\:{e}^{\mathrm{2}{x}} }{\left({e}^{\mathrm{2}{x}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${g}^{'} \left({x}\right)\:=\:\:\frac{\mathrm{4}\:{e}^{\mathrm{2}{x}} }{\left({e}^{\mathrm{2}{x}} \:+\mathrm{1}\right)^{\mathrm{2}} \frac{\sqrt{\left({e}^{\mathrm{2}{x}} \:+\mathrm{1}\right)^{\mathrm{2}} −\left({e}^{\mathrm{2}{x}} −\mathrm{1}\right)^{\mathrm{2}} }}{{e}^{\mathrm{2}{x}} \:+\mathrm{1}}}\:=\frac{\mathrm{4}\:{e}^{\mathrm{2}{x}} }{\left({e}^{\mathrm{2}{x}} \:+\mathrm{1}\right)\sqrt{{e}^{\mathrm{4}{x}} \:+\mathrm{2}{e}^{\mathrm{2}{x}} +\mathrm{1}−{e}^{\mathrm{4}{x}} +\mathrm{2}{e}^{\mathrm{2}{x}} −\mathrm{1}}} \\ $$$$=\frac{\mathrm{4}\:{e}^{\mathrm{2}{x}} }{\left(\mathrm{1}+{e}^{\mathrm{2}{x}} \right)\mathrm{2}{e}^{{x}} }\:=\frac{\mathrm{2}{e}^{{x}} }{\left(\mathrm{1}+\:{e}^{\mathrm{2}{x}} \right)}\:\Rightarrow{g}^{'} \left({x}\right)\:=\frac{\mathrm{2}{e}^{{x}} }{\left(\mathrm{1}+{e}^{\mathrm{2}{x}} \right)}\:. \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 11/Feb/19

1)y=x^x +(sinx)^(lnx) y=u+v (dy/dx)=(du/dx)+(dv/dx) u=x^x lnu=xlnx (1/u)(du/dx)=x×(1/x)+lnx×1 (du/dx)=x^x (1+lnx) v=(sinx)^(lnx) lnv=lnxln(sinx) (1/v)×(dv/dx)=lnx×(1/(sinx))×cosx+ln(sinx)×(1/x) (dv/dx)=(sinx)^(lnx) [cotxlnx+((ln(sinx))/x)] so answer is (du/dx)+(dv/dx) =x^x (1+lnx)+(sinx)^(lnx) [cotxlnx+((ln(sinx))/x)]

$$\left.\mathrm{1}\right){y}={x}^{{x}} +\left({sinx}\right)^{{lnx}} \\ $$$${y}={u}+{v} \\ $$$$\frac{{dy}}{{dx}}=\frac{{du}}{{dx}}+\frac{{dv}}{{dx}} \\ $$$${u}={x}^{{x}} \\ $$$${lnu}={xlnx} \\ $$$$\frac{\mathrm{1}}{{u}}\frac{{du}}{{dx}}={x}×\frac{\mathrm{1}}{{x}}+{lnx}×\mathrm{1} \\ $$$$\frac{{du}}{{dx}}={x}^{{x}} \left(\mathrm{1}+{lnx}\right) \\ $$$${v}=\left({sinx}\right)^{{lnx}} \\ $$$${lnv}={lnxln}\left({sinx}\right) \\ $$$$\frac{\mathrm{1}}{{v}}×\frac{{dv}}{{dx}}={lnx}×\frac{\mathrm{1}}{{sinx}}×{cosx}+{ln}\left({sinx}\right)×\frac{\mathrm{1}}{{x}} \\ $$$$\frac{{dv}}{{dx}}=\left({sinx}\right)^{{lnx}} \left[{cotxlnx}+\frac{{ln}\left({sinx}\right)}{{x}}\right] \\ $$$${so}\:{answer}\:{is} \\ $$$$\frac{{du}}{{dx}}+\frac{{dv}}{{dx}} \\ $$$$={x}^{{x}} \left(\mathrm{1}+{lnx}\right)+\left({sinx}\right)^{{lnx}} \left[{cotxlnx}+\frac{{ln}\left({sinx}\right)}{{x}}\right] \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 11/Feb/19

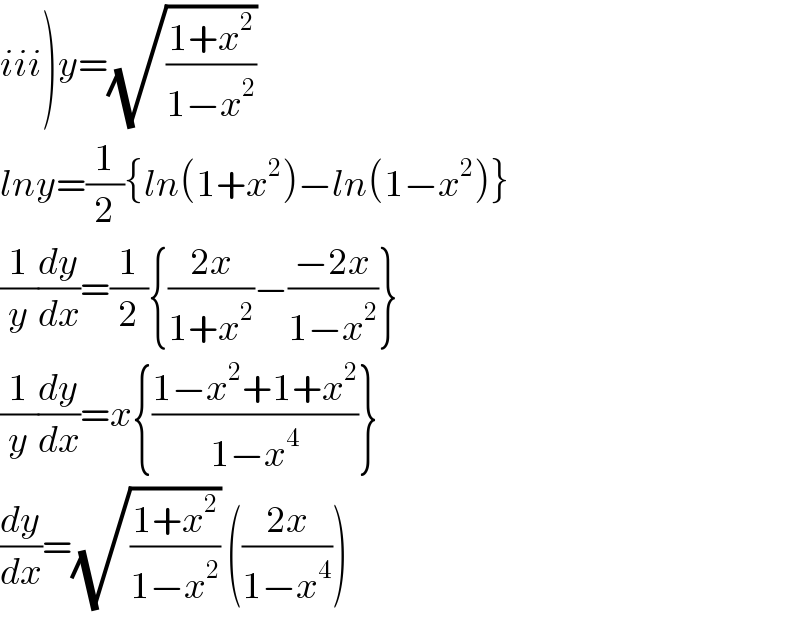
iii)y=(√((1+x^2 )/(1−x^2 ))) lny=(1/2){ln(1+x^2 )−ln(1−x^2 )} (1/y)(dy/dx)=(1/2){((2x)/(1+x^2 ))−((−2x)/(1−x^2 ))} (1/y)(dy/dx)=x{((1−x^2 +1+x^2 )/(1−x^4 ))} (dy/dx)=(√((1+x^2 )/(1−x^2 ))) (((2x)/(1−x^4 )))

$$\left.{iii}\right){y}=\sqrt{\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }}\: \\ $$$${lny}=\frac{\mathrm{1}}{\mathrm{2}}\left\{{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)−{ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\right\} \\ $$$$\frac{\mathrm{1}}{{y}}\frac{{dy}}{{dx}}=\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }−\frac{−\mathrm{2}{x}}{\mathrm{1}−{x}^{\mathrm{2}} }\right\} \\ $$$$\frac{\mathrm{1}}{{y}}\frac{{dy}}{{dx}}={x}\left\{\frac{\mathrm{1}−{x}^{\mathrm{2}} +\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{4}} }\right\} \\ $$$$\frac{{dy}}{{dx}}=\sqrt{\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }}\:\left(\frac{\mathrm{2}{x}}{\mathrm{1}−{x}^{\mathrm{4}} }\right) \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 11/Feb/19

ii)y=sin^(−1) (tanhx) (dy/dx)=(1/(√(1−(tanhx)^2 )))×sech^2 x

$$\left.{ii}\right){y}={sin}^{−\mathrm{1}} \left({tanhx}\right) \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{1}}{\sqrt{\mathrm{1}−\left({tanhx}\right)^{\mathrm{2}} }}×{sech}^{\mathrm{2}} {x} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com