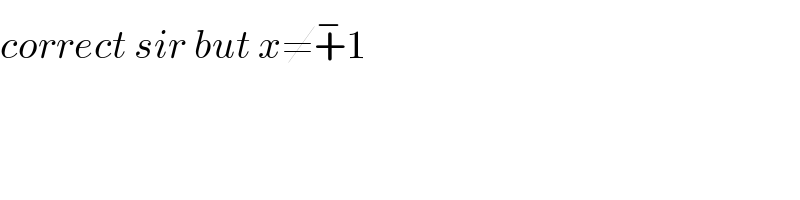Question and Answers Forum
Question Number 54808 by turbo msup by abdo last updated on 11/Feb/19
![let p(x)=(1+x^2 )(1+x^4 )...(1+x^2^n ) with n integr natural 1) find a simple form of p(x) 2) find roots of p(x)and decompose p(x) inside C[x] 3)calculate ∫_0 ^1 p(x)dx 4) decompose the fraction F(x)=(1/(p(x))) .](Q54808.png)
Commented by maxmathsup by imad last updated on 13/Feb/19
![1) we can use recurrence to prove that for x≠+^− 1 P(x) =((1−x^2^(n+1) )/(1−x^2 )) 2) P(z)=0 ⇔ 1−z^2^(n+1) =0 ⇔ 1−z^q =0 with m=2^(n+1) the roots of z^m =1 are z_k =e^((i2kπ)/m) with k ∈ [[0,m−1]] ⇒z_k =e^((i2kπ)/2^(n+1) ) = e^((ikπ)/2^n ) with k ∈[[0,2^(n+1) −1]] but but eliminate values of k /z_k ^2 =1 .](Q54873.png)
Commented by maxmathsup by imad last updated on 13/Feb/19
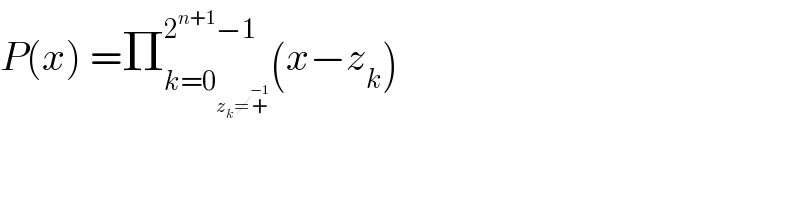
Answered by mr W last updated on 12/Feb/19
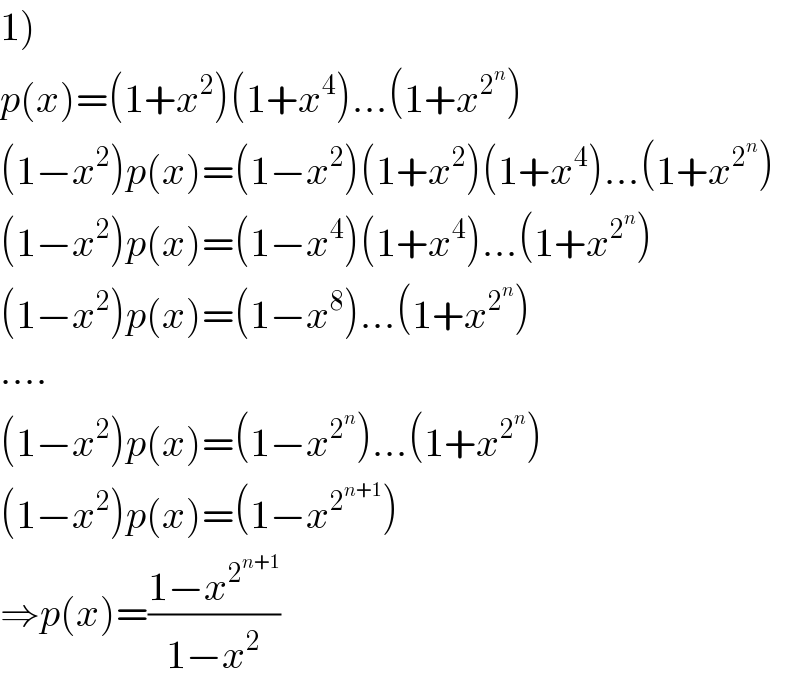
Commented by maxmathsup by imad last updated on 12/Feb/19