Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 54876 by shaddie last updated on 13/Feb/19

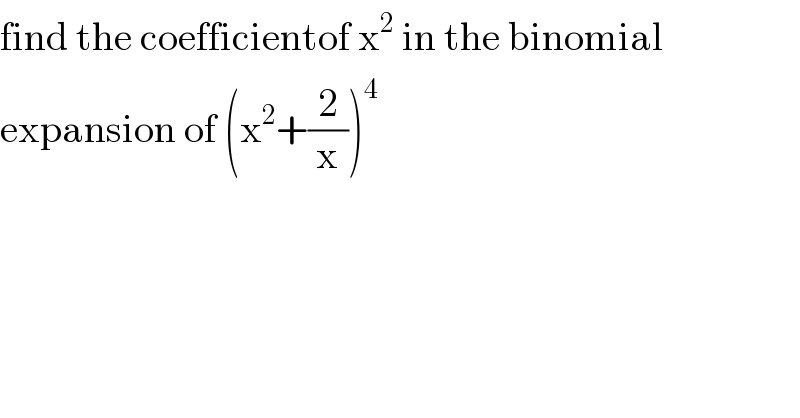
find the coefficientof x^2 in the binomial expansion of (x^2 +(2/x))^4

$$\mathrm{find}\:\mathrm{the}\:\mathrm{coefficientof}\:\mathrm{x}^{\mathrm{2}} \:\mathrm{in}\:\mathrm{the}\:\mathrm{binomial} \\ $$$$\mathrm{expansion}\:\mathrm{of}\:\left(\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{2}}{\mathrm{x}}\right)^{\mathrm{4}} \\ $$

Commented by maxmathsup by imad last updated on 13/Feb/19

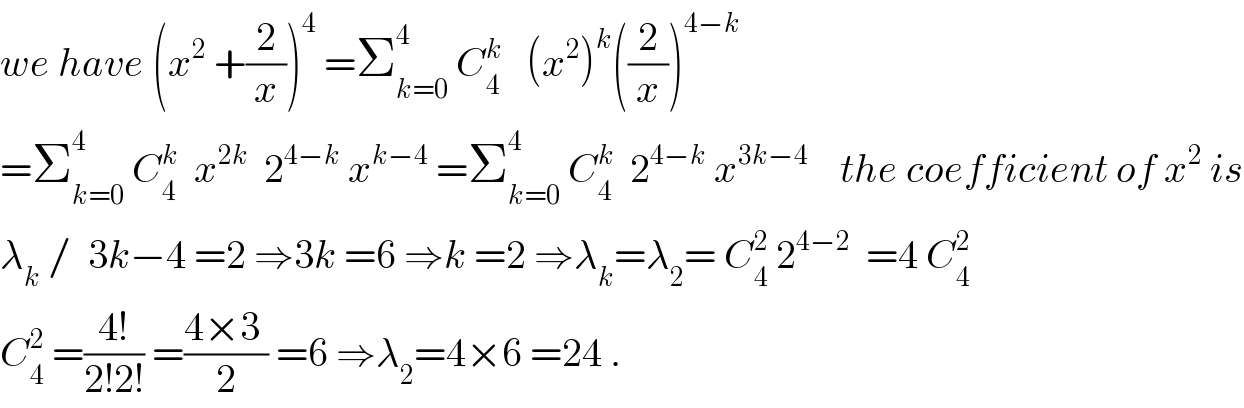
we have (x^2 +(2/x))^4 =Σ_(k=0) ^4 C_4 ^k (x^2 )^k ((2/x))^(4−k) =Σ_(k=0) ^4 C_4 ^k x^(2k) 2^(4−k) x^(k−4) =Σ_(k=0) ^4 C_4 ^k 2^(4−k) x^(3k−4) the coefficient of x^2 is λ_k / 3k−4 =2 ⇒3k =6 ⇒k =2 ⇒λ_k =λ_2 = C_4 ^2 2^(4−2) =4 C_4 ^2 C_4 ^2 =((4!)/(2!2!)) =((4×3 )/2) =6 ⇒λ_2 =4×6 =24 .

$${we}\:{have}\:\left({x}^{\mathrm{2}} \:+\frac{\mathrm{2}}{{x}}\right)^{\mathrm{4}} \:=\sum_{{k}=\mathrm{0}} ^{\mathrm{4}} \:{C}_{\mathrm{4}} ^{{k}} \:\:\:\left({x}^{\mathrm{2}} \right)^{{k}} \left(\frac{\mathrm{2}}{{x}}\right)^{\mathrm{4}−{k}} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{\mathrm{4}} \:{C}_{\mathrm{4}} ^{{k}} \:\:{x}^{\mathrm{2}{k}} \:\:\mathrm{2}^{\mathrm{4}−{k}} \:{x}^{{k}−\mathrm{4}} \:=\sum_{{k}=\mathrm{0}} ^{\mathrm{4}} \:{C}_{\mathrm{4}} ^{{k}} \:\:\mathrm{2}^{\mathrm{4}−{k}} \:{x}^{\mathrm{3}{k}−\mathrm{4}} \:\:\:\:{the}\:{coefficient}\:{of}\:{x}^{\mathrm{2}} \:{is} \\ $$$$\lambda_{{k}} \:/\:\:\mathrm{3}{k}−\mathrm{4}\:=\mathrm{2}\:\Rightarrow\mathrm{3}{k}\:=\mathrm{6}\:\Rightarrow{k}\:=\mathrm{2}\:\Rightarrow\lambda_{{k}} =\lambda_{\mathrm{2}} =\:{C}_{\mathrm{4}} ^{\mathrm{2}} \:\mathrm{2}^{\mathrm{4}−\mathrm{2}} \:\:=\mathrm{4}\:{C}_{\mathrm{4}} ^{\mathrm{2}} \\ $$$${C}_{\mathrm{4}} ^{\mathrm{2}} \:=\frac{\mathrm{4}!}{\mathrm{2}!\mathrm{2}!}\:=\frac{\mathrm{4}×\mathrm{3}\:}{\mathrm{2}}\:=\mathrm{6}\:\Rightarrow\lambda_{\mathrm{2}} =\mathrm{4}×\mathrm{6}\:=\mathrm{24}\:. \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 14/Feb/19

let r+1 th term contains x^2 4c_r (x^2 )^(4−r) ((2/x))^r 4c_r ×x^(8−2r) ×(2^r /x^r ) hence x^(8−2r−r) =x^2 −3r=2−8 →−3r=−6 r=2 4c_2 ×x^(8−3×2) ×2^2 → ((4!)/(2!2!))×4×x^2 so the coefficient is →6×4=24

$${let}\:{r}+\mathrm{1}\:{th}\:{term}\:{contains}\:{x}^{\mathrm{2}} \\ $$$$\mathrm{4}{c}_{{r}} \left({x}^{\mathrm{2}} \right)^{\mathrm{4}−{r}} \left(\frac{\mathrm{2}}{{x}}\right)^{{r}} \\ $$$$\mathrm{4}{c}_{{r}} ×{x}^{\mathrm{8}−\mathrm{2}{r}} ×\frac{\mathrm{2}^{{r}} }{{x}^{{r}} } \\ $$$${hence}\:{x}^{\mathrm{8}−\mathrm{2}{r}−{r}} ={x}^{\mathrm{2}} \\ $$$$−\mathrm{3}{r}=\mathrm{2}−\mathrm{8}\:\:\:\rightarrow−\mathrm{3}{r}=−\mathrm{6} \\ $$$${r}=\mathrm{2} \\ $$$$\mathrm{4}{c}_{\mathrm{2}} ×{x}^{\mathrm{8}−\mathrm{3}×\mathrm{2}} ×\mathrm{2}^{\mathrm{2}} \rightarrow\:\:\:\frac{\mathrm{4}!}{\mathrm{2}!\mathrm{2}!}×\mathrm{4}×{x}^{\mathrm{2}} \\ $$$${so}\:{the}\:{coefficient}\:{is}\:\rightarrow\mathrm{6}×\mathrm{4}=\mathrm{24} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com