
Question Number 5490 by 123456 last updated on 16/May/16
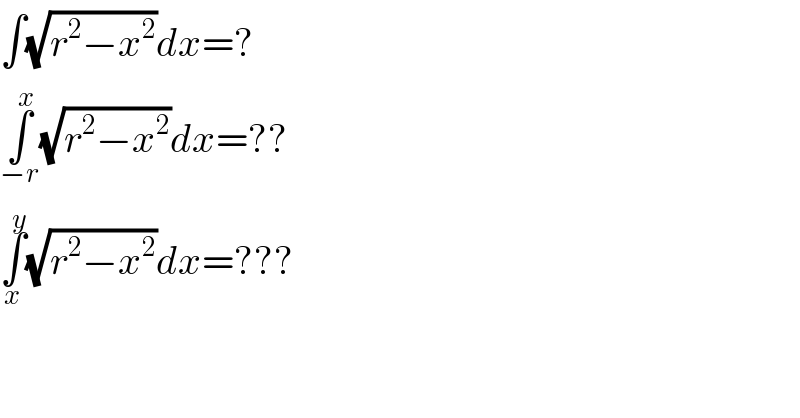
$$\int\sqrt{{r}^{\mathrm{2}} −{x}^{\mathrm{2}} }{dx}=? \\ $$$$\underset{−{r}} {\overset{{x}} {\int}}\sqrt{{r}^{\mathrm{2}} −{x}^{\mathrm{2}} }{dx}=?? \\ $$$$\underset{{x}} {\overset{{y}} {\int}}\sqrt{{r}^{\mathrm{2}} −{x}^{\mathrm{2}} }{dx}=??? \\ $$
Answered by FilupSmith last updated on 16/May/16
![let x=r∙sin(θ) ⇒ dx=cos(θ)dθ ∴θ=arcsin((x/r)) ∴∫(√(r^2 −x^2 ))dx=∫((√(r^2 −r^2 sin^2 θ ))cosθ)dθ =∫cosθ(√(r^2 (1−sin^2 θ)))dθ =∫rcosθ(√(cos^2 θ))dθ =r∫cos^2 θdθ cos^2 (x)=((cos(2x)+1)/2) =r∫(1/2)(cos(2θ)+1)dθ =(r/2)((1/2)sin(2θ)+θ)+c ∴∫(√(r^2 −x^2 ))dx=(1/4)r∙sin(2∙arcsin((x/r)))+(1/2)r∙arcsin((x/r))+c −−−−−−−−−−−−−− ∫_(−r) ^x (√(r^2 −x^2 ))dx=(r/2)[(1/2)sin(2∙arcsin((x/r)))+arcsin((x/r))]_(−r) ^x =(r/2)[(1/2)sin(2∙arcsin((x/r)))+arcsin((x/r))−(1/2)sin(2∙arcsin(((−r)/r)))+r∙arcsin(((−r)/r))] =(r/2)[(1/2)sin(2∙arcsin((x/r)))+r∙arcsin((x/r))−(1/2)sin(−π)+(π/2)] ∴∫_(−r) ^x (√(r^2 −x^2 ))dx=(r/2)[(1/2)sin(2∙arcsin((x/r)))+r∙arcsin((x/r))+(π/2)]](Q5494.png)
$$\mathrm{let}\:{x}={r}\centerdot\mathrm{sin}\left(\theta\right)\:\Rightarrow\:{dx}=\mathrm{cos}\left(\theta\right){d}\theta \\ $$$$\:\:\:\:\:\:\:\therefore\theta=\mathrm{arcsin}\left(\frac{{x}}{{r}}\right) \\ $$$$\therefore\int\sqrt{{r}^{\mathrm{2}} −{x}^{\mathrm{2}} }{dx}=\int\left(\sqrt{{r}^{\mathrm{2}} −{r}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \theta\:}\mathrm{cos}\theta\right){d}\theta \\ $$$$=\int\mathrm{cos}\theta\sqrt{{r}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \theta\right)}{d}\theta \\ $$$$=\int{r}\mathrm{cos}\theta\sqrt{\mathrm{cos}^{\mathrm{2}} \theta}{d}\theta \\ $$$$={r}\int\mathrm{cos}^{\mathrm{2}} \theta{d}\theta \\ $$$$\mathrm{cos}^{\mathrm{2}} \left({x}\right)=\frac{\mathrm{cos}\left(\mathrm{2}{x}\right)+\mathrm{1}}{\mathrm{2}} \\ $$$$={r}\int\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos}\left(\mathrm{2}\theta\right)+\mathrm{1}\right){d}\theta \\ $$$$=\frac{{r}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2}\theta\right)+\theta\right)+{c} \\ $$$$\therefore\int\sqrt{{r}^{\mathrm{2}} −{x}^{\mathrm{2}} }{dx}=\frac{\mathrm{1}}{\mathrm{4}}{r}\centerdot\mathrm{sin}\left(\mathrm{2}\centerdot\mathrm{arcsin}\left(\frac{{x}}{{r}}\right)\right)+\frac{\mathrm{1}}{\mathrm{2}}{r}\centerdot\mathrm{arcsin}\left(\frac{{x}}{{r}}\right)+{c} \\ $$$$ \\ $$$$−−−−−−−−−−−−−− \\ $$$$\underset{−{r}} {\overset{{x}} {\int}}\sqrt{{r}^{\mathrm{2}} −{x}^{\mathrm{2}} }{dx}=\frac{{r}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2}\centerdot\mathrm{arcsin}\left(\frac{{x}}{{r}}\right)\right)+\mathrm{arcsin}\left(\frac{{x}}{{r}}\right)\right]_{−{r}} ^{{x}} \\ $$$$=\frac{{r}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2}\centerdot\mathrm{arcsin}\left(\frac{{x}}{{r}}\right)\right)+\mathrm{arcsin}\left(\frac{{x}}{{r}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2}\centerdot\mathrm{arcsin}\left(\frac{−{r}}{{r}}\right)\right)+{r}\centerdot\mathrm{arcsin}\left(\frac{−{r}}{{r}}\right)\right] \\ $$$$=\frac{{r}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2}\centerdot\mathrm{arcsin}\left(\frac{{x}}{{r}}\right)\right)+{r}\centerdot\mathrm{arcsin}\left(\frac{{x}}{{r}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(−\pi\right)+\frac{\pi}{\mathrm{2}}\right] \\ $$$$\therefore\underset{−{r}} {\overset{{x}} {\int}}\sqrt{{r}^{\mathrm{2}} −{x}^{\mathrm{2}} }{dx}=\frac{{r}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2}\centerdot\mathrm{arcsin}\left(\frac{{x}}{{r}}\right)\right)+{r}\centerdot\mathrm{arcsin}\left(\frac{{x}}{{r}}\right)+\frac{\pi}{\mathrm{2}}\right] \\ $$
