
Question and Answers Forum
Question Number 54936 by maxmathsup by imad last updated on 14/Feb/19
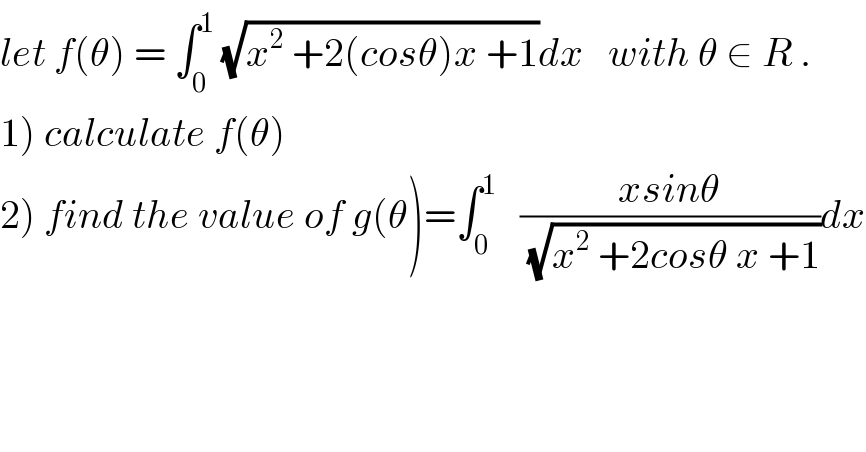
Commented by Abdo msup. last updated on 16/Feb/19
![1) we have f(θ)=∫_0 ^1 (√(x^(2 ) +2cosθ x +1))dx =∫_0 ^1 (√((x+cosθ)^2 +sin^2 θ))dθ chang.x+cosθ=sinθ t give f(θ)=∫_(coatanθ) ^(cotan((θ/2))) ∣sinθ∣sinθ (√(1+t^2 ))dt f(θ)=∣sinθ∣sinθ ∫_(cotan(θ)) ^(cotan((θ/2))) (√(1+t^2 ))dt let find ∫ (√(1+t^2 ))dt changement t=sh(u)give ∫ (√(1+t^2 ))dt =∫ ch(u)ch(u)du =∫ ch^2 (u)du =∫ ((1+ch(2u))/2)du =(u/2) +(1/4)sh(2u) =(u/2) +(1/2)ch(u)sh(u) =(1/2)argsh(t) +(1/2)t(√(1+t^2 )) +c =(1/2)ln(t +(√(1+t^2 ))) +(t/2)(√(1+t^2 )) ⇒ ∫_(cotan(θ)) ^(cotan((θ/2))) (√(1+t^2 ))dt =(1/2)[ln(t+(√(1+t^2 ))) +t(√(1+t^2 ))]_(cotanθ) ^(cotan((θ/2))) =(1/2){ln(cotan((θ/2))+(√(1+cotan^2 ((θ/2))))) +cotan((θ/2))(√(1+cotan^2 ((θ/2))))−ln(cotanθ+(√(1+cotanθ)) −cotanθ(√(1+cotan^2 θ)))](Q55053.png)
Answered by tanmay.chaudhury50@gmail.com last updated on 15/Feb/19
![∫(√(x^2 +2xcosθ+1)) dx ∫(√((x+cosθ)^2 +sin^2 θ)) dx (((x+cosθ))/2)(√((x+cosθ)^2 +sin^2 θ)) +((sin^2 θ)/2)(√((x+cosθ)^2 +sin^2 θ)) +c so answer is ∣(((x+cosθ))/2)(√((x+cosθ)^2 +sin^2 θ)) +((sin^2 θ)/2)(√((x+cosθ)^2 +sin^2 θ)) ∣_0 ^1 [{(((1+cosθ))/2)(√((1+cosθ)^2 +sin^2 θ)) +((sin^2 θ)/2)(√((1+cosθ)^2 +sin^2 θ)) }−{((cosθ)/2)(√(cos^2 θ+sin^2 θ)) +((sin^2 θ)/2)×(√(cos^2 θ+sin^2 θ)) }] [(((1+cosθ))/2)(√(1+2cosθ+1)) +((sin^2 θ)/2)(√(2+2cosθ)) }−{((cosθ)/2)+((sin^2 θ)/2)}] (((1+cosθ))/2)×2cos(θ/2)+((sin^2 θ)/2)×2cos(θ/2)−((cosθ)/2)−((sin^2 θ)/2)] check upto this...](Q54982.png)
| ||
Question and Answers Forum | ||
Question Number 54936 by maxmathsup by imad last updated on 14/Feb/19 | ||
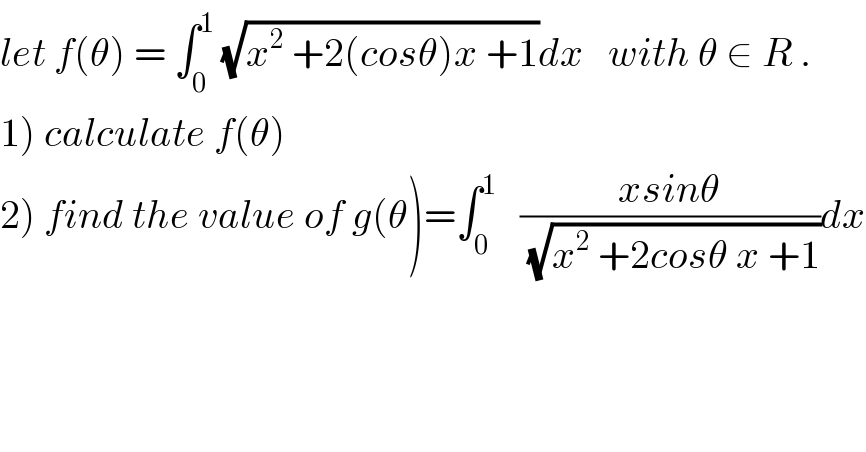 | ||
Commented by Abdo msup. last updated on 16/Feb/19 | ||
![1) we have f(θ)=∫_0 ^1 (√(x^(2 ) +2cosθ x +1))dx =∫_0 ^1 (√((x+cosθ)^2 +sin^2 θ))dθ chang.x+cosθ=sinθ t give f(θ)=∫_(coatanθ) ^(cotan((θ/2))) ∣sinθ∣sinθ (√(1+t^2 ))dt f(θ)=∣sinθ∣sinθ ∫_(cotan(θ)) ^(cotan((θ/2))) (√(1+t^2 ))dt let find ∫ (√(1+t^2 ))dt changement t=sh(u)give ∫ (√(1+t^2 ))dt =∫ ch(u)ch(u)du =∫ ch^2 (u)du =∫ ((1+ch(2u))/2)du =(u/2) +(1/4)sh(2u) =(u/2) +(1/2)ch(u)sh(u) =(1/2)argsh(t) +(1/2)t(√(1+t^2 )) +c =(1/2)ln(t +(√(1+t^2 ))) +(t/2)(√(1+t^2 )) ⇒ ∫_(cotan(θ)) ^(cotan((θ/2))) (√(1+t^2 ))dt =(1/2)[ln(t+(√(1+t^2 ))) +t(√(1+t^2 ))]_(cotanθ) ^(cotan((θ/2))) =(1/2){ln(cotan((θ/2))+(√(1+cotan^2 ((θ/2))))) +cotan((θ/2))(√(1+cotan^2 ((θ/2))))−ln(cotanθ+(√(1+cotanθ)) −cotanθ(√(1+cotan^2 θ)))](Q55053.png) | ||
Answered by tanmay.chaudhury50@gmail.com last updated on 15/Feb/19 | ||
![∫(√(x^2 +2xcosθ+1)) dx ∫(√((x+cosθ)^2 +sin^2 θ)) dx (((x+cosθ))/2)(√((x+cosθ)^2 +sin^2 θ)) +((sin^2 θ)/2)(√((x+cosθ)^2 +sin^2 θ)) +c so answer is ∣(((x+cosθ))/2)(√((x+cosθ)^2 +sin^2 θ)) +((sin^2 θ)/2)(√((x+cosθ)^2 +sin^2 θ)) ∣_0 ^1 [{(((1+cosθ))/2)(√((1+cosθ)^2 +sin^2 θ)) +((sin^2 θ)/2)(√((1+cosθ)^2 +sin^2 θ)) }−{((cosθ)/2)(√(cos^2 θ+sin^2 θ)) +((sin^2 θ)/2)×(√(cos^2 θ+sin^2 θ)) }] [(((1+cosθ))/2)(√(1+2cosθ+1)) +((sin^2 θ)/2)(√(2+2cosθ)) }−{((cosθ)/2)+((sin^2 θ)/2)}] (((1+cosθ))/2)×2cos(θ/2)+((sin^2 θ)/2)×2cos(θ/2)−((cosθ)/2)−((sin^2 θ)/2)] check upto this...](Q54982.png) | ||
| ||