
Question and Answers Forum
Question Number 54972 by peter frank last updated on 15/Feb/19
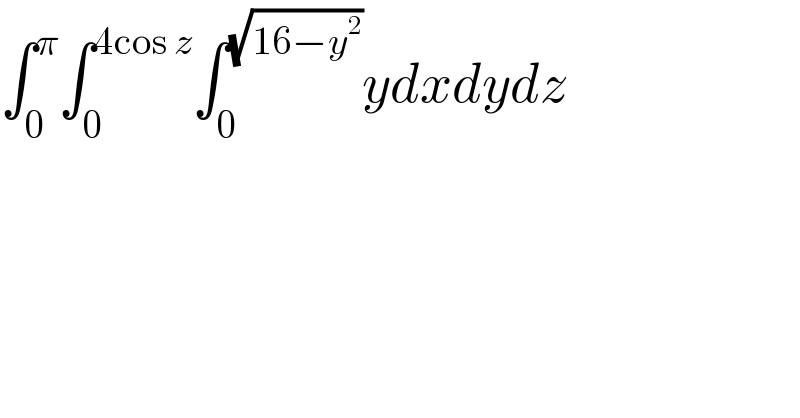
Answered by kaivan.ahmadi last updated on 15/Feb/19
![∫_0 ^π ∫_0 ^(4cosz) y x]_0 ^(√(16−y^2 )) dydz= ∫_0 ^π ∫_0 ^(4cosz) (y(√(16−y^2 )))dydz= ∫_0 ^π ((−1)/3)(16−y^2 )^(3/2) ]_0 ^(4cosz) dz= ((−1)/3)∫_0 ^π ((16−16cos^2 z)^(3/2) −16^(3/2) )dz= ((−16^(3/2) )/3)∫_0 ^π (sin^3 z−1)dz=((−16^(3/2) )/3)×(((sin^2 zcosz+2cosz)/3)−z)_0 ^π = ((16^(3/2) )/3)×[(((−2)/3)−π)−((2/3))]= ((−16^(3/2) )/3)×(((−4)/3)−π)=((256)/9)+((64)/3)π](Q54976.png)
| ||
Question and Answers Forum | ||
Question Number 54972 by peter frank last updated on 15/Feb/19 | ||
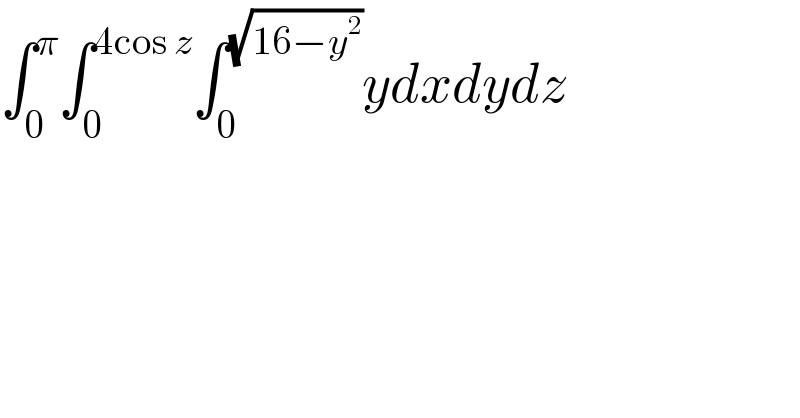 | ||
Answered by kaivan.ahmadi last updated on 15/Feb/19 | ||
![∫_0 ^π ∫_0 ^(4cosz) y x]_0 ^(√(16−y^2 )) dydz= ∫_0 ^π ∫_0 ^(4cosz) (y(√(16−y^2 )))dydz= ∫_0 ^π ((−1)/3)(16−y^2 )^(3/2) ]_0 ^(4cosz) dz= ((−1)/3)∫_0 ^π ((16−16cos^2 z)^(3/2) −16^(3/2) )dz= ((−16^(3/2) )/3)∫_0 ^π (sin^3 z−1)dz=((−16^(3/2) )/3)×(((sin^2 zcosz+2cosz)/3)−z)_0 ^π = ((16^(3/2) )/3)×[(((−2)/3)−π)−((2/3))]= ((−16^(3/2) )/3)×(((−4)/3)−π)=((256)/9)+((64)/3)π](Q54976.png) | ||
| ||