
Question and Answers Forum
Question Number 54983 by ajfour last updated on 15/Feb/19
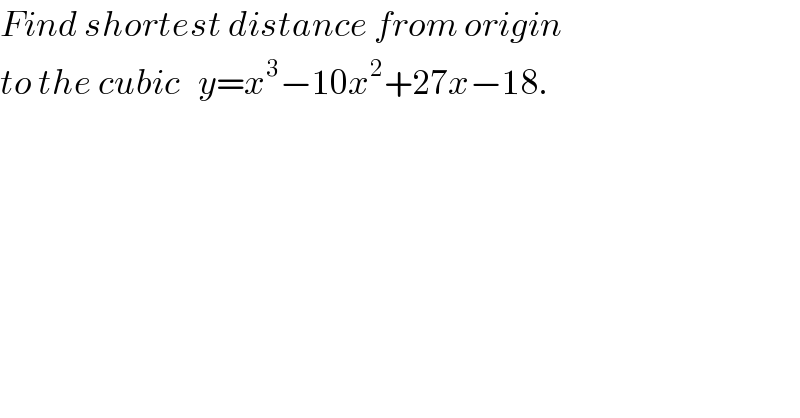
Commented by mr W last updated on 15/Feb/19

Commented by ajfour last updated on 15/Feb/19
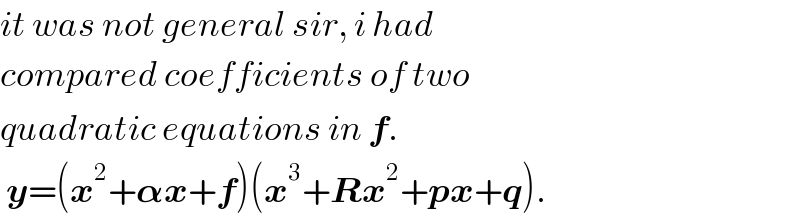
Answered by mr W last updated on 16/Feb/19

Commented by mr W last updated on 16/Feb/19
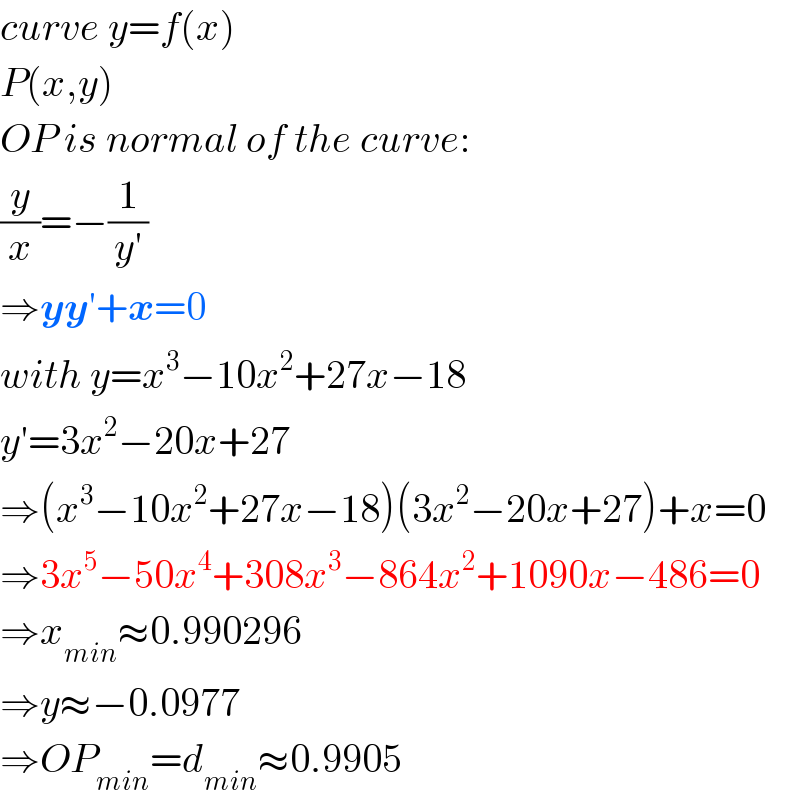
Commented by mr W last updated on 16/Feb/19

Commented by mr W last updated on 16/Feb/19
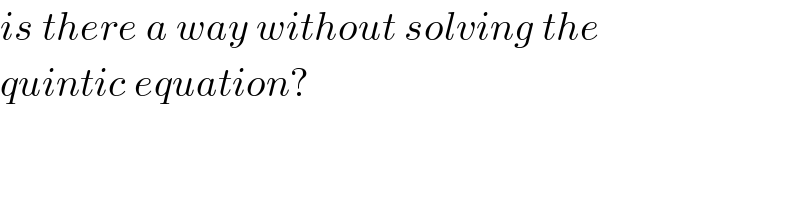
Commented by mr W last updated on 16/Feb/19
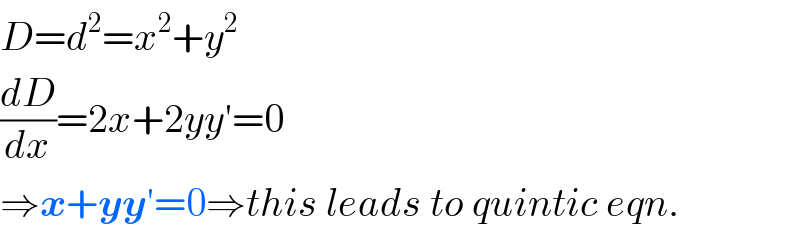
Commented by MJS last updated on 16/Feb/19
![no Sir. we can also go this way: (d/dx)[f(x)^2 +x^2 ]=0 which also leads to a quintic with at least no easy exact solution](Q55026.png)
Commented by ajfour last updated on 16/Feb/19

