Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 55030 by Joel578 last updated on 16/Feb/19

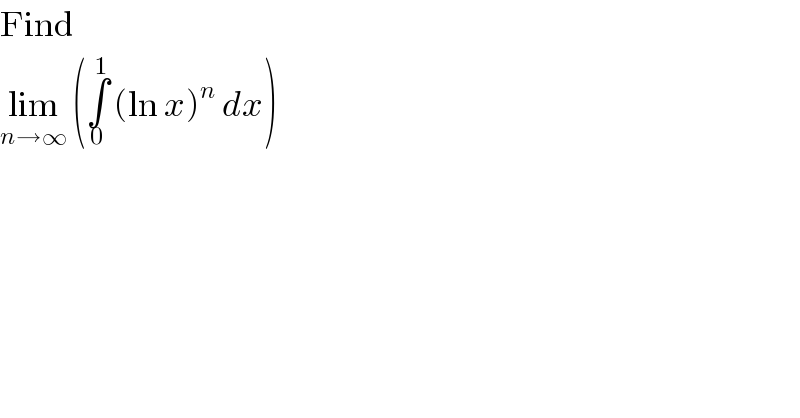
Find lim_(n→∞) (∫_0 ^1 (ln x)^n dx)

$$\mathrm{Find} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\left(\mathrm{ln}\:{x}\right)^{{n}} \:{dx}\right) \\ $$

Commented by tm888 last updated on 16/Feb/19

is[.]any g.i.f

$${is}\left[.\right]{any}\:{g}.{i}.{f} \\ $$

Commented by Joel578 last updated on 16/Feb/19

sorry. it′s only a bracket

$$\mathrm{sorry}.\:\mathrm{it}'\mathrm{s}\:\mathrm{only}\:\mathrm{a}\:\mathrm{bracket} \\ $$

Commented by tm888 last updated on 16/Feb/19

Commented by maxmathsup by imad last updated on 16/Feb/19

let A_n =∫_0 ^1 (lnx)^n dx changement ln(x)=−t give x=e^(−t) A_n = ∫_0 ^(+∞) (−t)^n e^(−t) dt =(−1)^n ∫_0 ^∞ t^n e^(−t) dt by parts W_n =∫_0 ^∞ t^n e^(−t) dt =[−t^n e^(−t) ]_0 ^(+∞) +∫_0 ^∞ n t^(n−1) e^(−t) dt =nW_(n−1) ⇒W_n =n! ⇒ A_n =(−1)^n n! ⇒A_(2n) =(2n)! →+∞(n→+∞) and A_(2n+1) =−(2n+1)! →−∞ (n→+∞) so the sequence A_n is divergent . also we can see that ∫_0 ^∞ t^n e^(−t) dt =Γ(n+1)=n!

$${let}\:{A}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \left({lnx}\right)^{{n}} {dx}\:\:{changement}\:{ln}\left({x}\right)=−{t}\:{give}\:\:{x}={e}^{−{t}} \\ $$$${A}_{{n}} =\:\int_{\mathrm{0}} ^{+\infty} \left(−{t}\right)^{{n}} \:\:{e}^{−{t}} \:{dt}\:=\left(−\mathrm{1}\right)^{{n}} \:\int_{\mathrm{0}} ^{\infty} \:{t}^{{n}} \:{e}^{−{t}} \:{dt}\:\:\:{by}\:{parts}\: \\ $$$${W}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:{t}^{{n}} \:{e}^{−{t}} \:{dt}\:=\left[−{t}^{{n}} \:{e}^{−{t}} \right]_{\mathrm{0}} ^{+\infty} \:+\int_{\mathrm{0}} ^{\infty} \:{n}\:{t}^{{n}−\mathrm{1}} \:\:\:{e}^{−{t}} \:{dt} \\ $$$$={nW}_{{n}−\mathrm{1}} \:\:\:\Rightarrow{W}_{{n}} ={n}!\:\Rightarrow\:{A}_{{n}} =\left(−\mathrm{1}\right)^{{n}} {n}!\:\Rightarrow{A}_{\mathrm{2}{n}} =\left(\mathrm{2}{n}\right)!\:\rightarrow+\infty\left({n}\rightarrow+\infty\right) \\ $$$${and}\:{A}_{\mathrm{2}{n}+\mathrm{1}} =−\left(\mathrm{2}{n}+\mathrm{1}\right)!\:\rightarrow−\infty\:\left({n}\rightarrow+\infty\right)\:{so}\:{the}\:{sequence}\:{A}_{{n}} {is}\:{divergent}\:. \\ $$$${also}\:{we}\:{can}\:{see}\:{that}\:\int_{\mathrm{0}} ^{\infty} \:{t}^{{n}} \:{e}^{−{t}} \:{dt}\:=\Gamma\left({n}+\mathrm{1}\right)={n}! \\ $$

Commented by tm888 last updated on 16/Feb/19

Answered by tanmay.chaudhury50@gmail.com last updated on 16/Feb/19

∫(lnx)^n dx (lnx)^n x−∫n(lnx)^(n−1) (1/x)×xdx I_n =∣x(lnx)^n ∣_0 ^1 −n∫_0 ^1 (lnx)^(n−1) dx I_n =−nI_(n−1) I_0 =1 I_1 =−1 I_2 =−2×(−1)=2×1=(−1)^2 ×2! I_3 =−3×2=−3×2×1=(−1)^3 ×3! I_4 =−4×(−3×2)=4×3×2×1=(−1)^4 ×4! thus... I_n =(−)^n n! lim_(n→∞) (−1)^n n! →∞ let other calculate... lim_(n→∞) li_(n→∞)

$$\int\left({lnx}\right)^{{n}} {dx} \\ $$$$\left({lnx}\right)^{{n}} {x}−\int{n}\left({lnx}\right)^{{n}−\mathrm{1}} \frac{\mathrm{1}}{{x}}×{xdx} \\ $$$${I}_{{n}} =\mid{x}\left({lnx}\right)^{{n}} \mid_{\mathrm{0}} ^{\mathrm{1}} −{n}\int_{\mathrm{0}} ^{\mathrm{1}} \left({lnx}\right)^{{n}−\mathrm{1}} {dx} \\ $$$${I}_{{n}} =−{nI}_{{n}−\mathrm{1}} \\ $$$${I}_{\mathrm{0}} =\mathrm{1} \\ $$$${I}_{\mathrm{1}} =−\mathrm{1} \\ $$$${I}_{\mathrm{2}} =−\mathrm{2}×\left(−\mathrm{1}\right)=\mathrm{2}×\mathrm{1}=\left(−\mathrm{1}\right)^{\mathrm{2}} ×\mathrm{2}! \\ $$$${I}_{\mathrm{3}} =−\mathrm{3}×\mathrm{2}=−\mathrm{3}×\mathrm{2}×\mathrm{1}=\left(−\mathrm{1}\right)^{\mathrm{3}} ×\mathrm{3}! \\ $$$${I}_{\mathrm{4}} =−\mathrm{4}×\left(−\mathrm{3}×\mathrm{2}\right)=\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{1}=\left(−\mathrm{1}\right)^{\mathrm{4}} ×\mathrm{4}! \\ $$$${thus}... \\ $$$${I}_{{n}} =\left(−\right)^{{n}} {n}! \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left(−\mathrm{1}\right)^{{n}} {n}!\:\rightarrow\infty \\ $$$$ \\ $$$$\boldsymbol{{let}}\:\boldsymbol{{other}}\:\boldsymbol{{calculate}}... \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{li}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com