
Question Number 55069 by gunawan last updated on 17/Feb/19
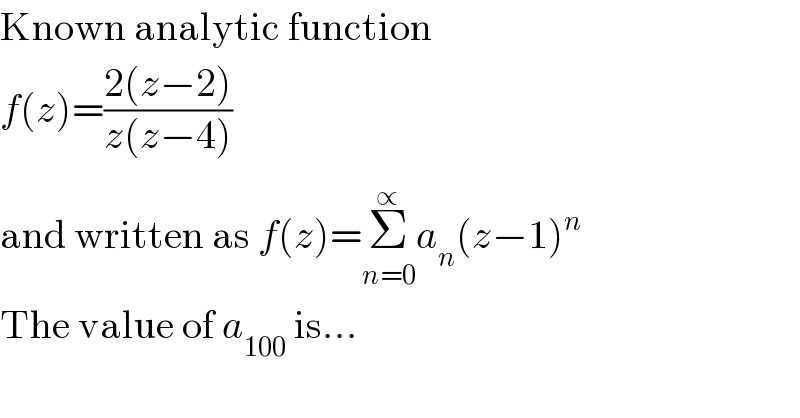
$$\mathrm{Known}\:\mathrm{analytic}\:\mathrm{function} \\ $$$${f}\left({z}\right)=\frac{\mathrm{2}\left({z}−\mathrm{2}\right)}{{z}\left({z}−\mathrm{4}\right)} \\ $$$$\mathrm{and}\:\mathrm{written}\:\mathrm{as}\:{f}\left({z}\right)=\underset{{n}=\mathrm{0}} {\overset{\propto} {\Sigma}}\:{a}_{{n}} \left({z}−\mathrm{1}\right)^{{n}} \\ $$$$\mathrm{The}\:\mathrm{value}\:\mathrm{of}\:{a}_{\mathrm{100}} \:\mathrm{is}... \\ $$
Commented by maxmathsup by imad last updated on 17/Feb/19
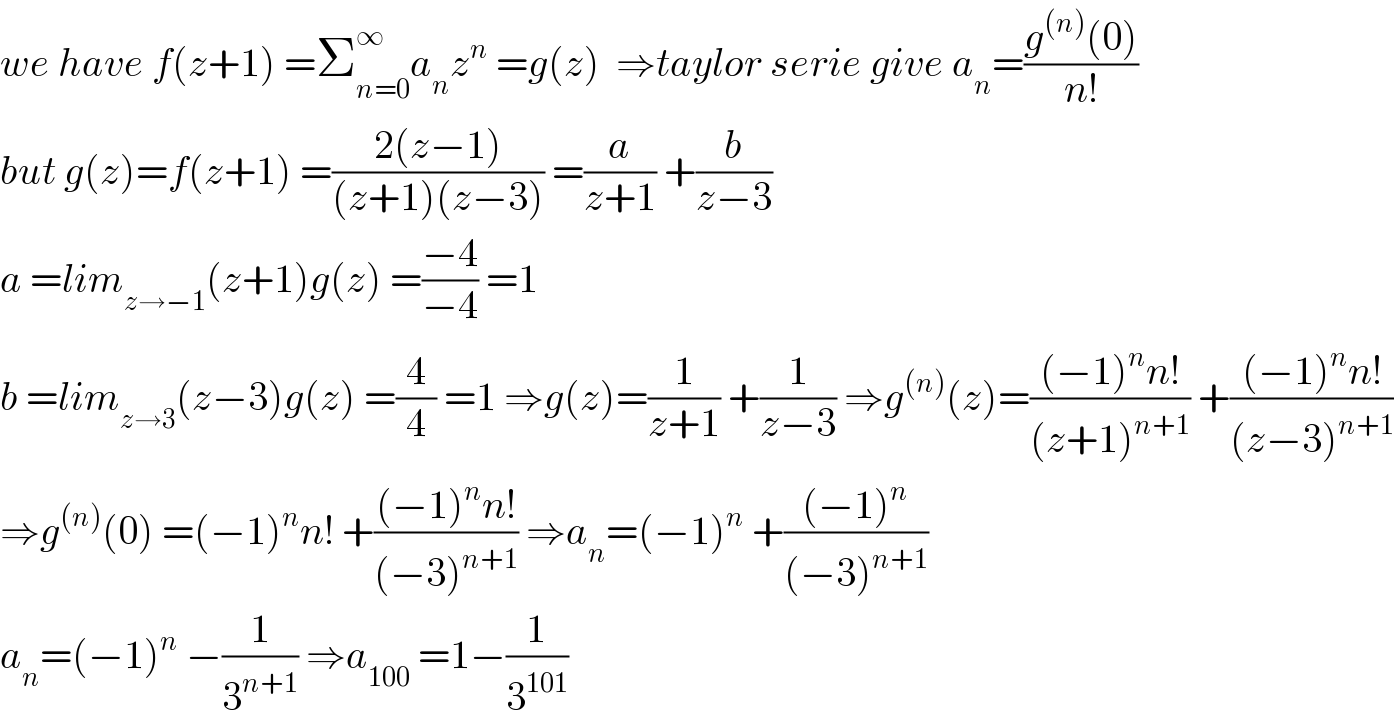
$${we}\:{have}\:{f}\left({z}+\mathrm{1}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} {a}_{{n}} {z}^{{n}} \:={g}\left({z}\right)\:\:\Rightarrow{taylor}\:{serie}\:{give}\:{a}_{{n}} =\frac{{g}^{\left({n}\right)} \left(\mathrm{0}\right)}{{n}!} \\ $$$${but}\:{g}\left({z}\right)={f}\left({z}+\mathrm{1}\right)\:=\frac{\mathrm{2}\left({z}−\mathrm{1}\right)}{\left({z}+\mathrm{1}\right)\left({z}−\mathrm{3}\right)}\:=\frac{{a}}{{z}+\mathrm{1}}\:+\frac{{b}}{{z}−\mathrm{3}} \\ $$$${a}\:={lim}_{{z}\rightarrow−\mathrm{1}} \left({z}+\mathrm{1}\right){g}\left({z}\right)\:=\frac{−\mathrm{4}}{−\mathrm{4}}\:=\mathrm{1} \\ $$$${b}\:={lim}_{{z}\rightarrow\mathrm{3}} \left({z}−\mathrm{3}\right){g}\left({z}\right)\:=\frac{\mathrm{4}}{\mathrm{4}}\:=\mathrm{1}\:\Rightarrow{g}\left({z}\right)=\frac{\mathrm{1}}{{z}+\mathrm{1}}\:+\frac{\mathrm{1}}{{z}−\mathrm{3}}\:\Rightarrow{g}^{\left({n}\right)} \left({z}\right)=\frac{\left(−\mathrm{1}\right)^{{n}} {n}!}{\left({z}+\mathrm{1}\right)^{{n}+\mathrm{1}} }\:+\frac{\left(−\mathrm{1}\right)^{{n}} {n}!}{\left({z}−\mathrm{3}\right)^{{n}+\mathrm{1}} } \\ $$$$\Rightarrow{g}^{\left({n}\right)} \left(\mathrm{0}\right)\:=\left(−\mathrm{1}\right)^{{n}} {n}!\:+\frac{\left(−\mathrm{1}\right)^{{n}} {n}!}{\left(−\mathrm{3}\right)^{{n}+\mathrm{1}} }\:\Rightarrow{a}_{{n}} =\left(−\mathrm{1}\right)^{{n}} \:+\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(−\mathrm{3}\right)^{{n}+\mathrm{1}} } \\ $$$${a}_{{n}} =\left(−\mathrm{1}\right)^{{n}} \:−\frac{\mathrm{1}}{\mathrm{3}^{{n}+\mathrm{1}} }\:\Rightarrow{a}_{\mathrm{100}} \:=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{101}} } \\ $$
Commented by mr W last updated on 17/Feb/19

$${thanks}\:{sir}! \\ $$
Commented by maxmathsup by imad last updated on 17/Feb/19
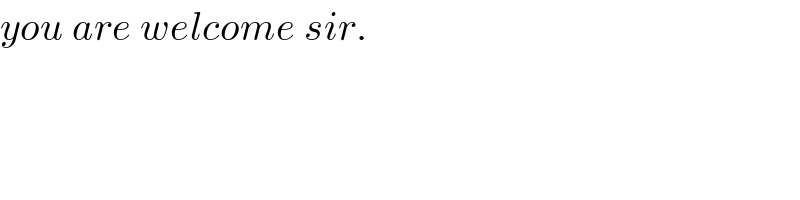
$${you}\:{are}\:{welcome}\:{sir}. \\ $$
Answered by mr W last updated on 17/Feb/19
![f(z)=((2(z−2))/(z(z−4)))=((2[(z−1)−1])/([(z−1)+1][(z−1)−3])) let t=z−1 f(z)=−((2(t−1))/(3(1+t)(1−(t/3)))) (1/(1+t))=Σ_(k=0) ^∞ (−t)^k =Σ_(k=0) ^∞ (−1)^k t^k (1/(1−(t/3)))=Σ_(k=9) ^∞ ((t/3))^k =Σ_(k=0) ^∞ (t^k /3^k ) f(z)=−(2/3)(t−1)[Σ_(k=0) ^∞ (−1)^k t^k ][Σ_(k=0) ^∞ (t^k /3^k )]=Σ_(n=0) ^∞ a_n t^n =Σ_(n=0) ^∞ a_n (z−1)^n a_(100) =−(2/3){Σ_(k=0) ^(99) (((−1)^(99−k) )/3^k )−Σ_(k=0) ^(100) (((−1)^(100−k) )/3^k )} a_(100) =−(2/3){2Σ_(k=0) ^(99) (((−1)^(99−k) )/3^k )−(1/3^(100) )} a_(100) =−(2/3){2(−(1/3^0 )+(1/3^1 )−(1/3^2 )+...+(1/3^(99) ))−(1/3^(100) )} a_(100) =−(2/3){2(−((1−(−(1/3))^(100) )/(1−(−(1/3)))))−(1/3^(100) )} a_(100) =−(2/3){−(3/2)[1−(1/3^(100) )]−(1/3^(100) )} a_(100) =−(2/3){−(3/2)+(1/(2×3^(100) ))} ⇒a_(100) =1−(1/3^(101) ) in general a_n =(−1)^n −(1/3^(n+1) )](Q55077.png)
$${f}\left({z}\right)=\frac{\mathrm{2}\left({z}−\mathrm{2}\right)}{{z}\left({z}−\mathrm{4}\right)}=\frac{\mathrm{2}\left[\left({z}−\mathrm{1}\right)−\mathrm{1}\right]}{\left[\left({z}−\mathrm{1}\right)+\mathrm{1}\right]\left[\left({z}−\mathrm{1}\right)−\mathrm{3}\right]} \\ $$$${let}\:{t}={z}−\mathrm{1} \\ $$$${f}\left({z}\right)=−\frac{\mathrm{2}\left({t}−\mathrm{1}\right)}{\mathrm{3}\left(\mathrm{1}+{t}\right)\left(\mathrm{1}−\frac{{t}}{\mathrm{3}}\right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+{t}}=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−{t}\right)^{{k}} =\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{k}} {t}^{{k}} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}−\frac{{t}}{\mathrm{3}}}=\underset{{k}=\mathrm{9}} {\overset{\infty} {\sum}}\left(\frac{{t}}{\mathrm{3}}\right)^{{k}} =\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{t}^{{k}} }{\mathrm{3}^{{k}} } \\ $$$${f}\left({z}\right)=−\frac{\mathrm{2}}{\mathrm{3}}\left({t}−\mathrm{1}\right)\left[\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{k}} {t}^{{k}} \right]\left[\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{t}^{{k}} }{\mathrm{3}^{{k}} }\right]=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{a}_{{n}} {t}^{{n}} =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{a}_{{n}} \left({z}−\mathrm{1}\right)^{{n}} \\ $$$${a}_{\mathrm{100}} =−\frac{\mathrm{2}}{\mathrm{3}}\left\{\underset{{k}=\mathrm{0}} {\overset{\mathrm{99}} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{99}−{k}} }{\mathrm{3}^{{k}} }−\underset{{k}=\mathrm{0}} {\overset{\mathrm{100}} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{100}−{k}} }{\mathrm{3}^{{k}} }\right\} \\ $$$${a}_{\mathrm{100}} =−\frac{\mathrm{2}}{\mathrm{3}}\left\{\mathrm{2}\underset{{k}=\mathrm{0}} {\overset{\mathrm{99}} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{99}−{k}} }{\mathrm{3}^{{k}} }−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{100}} }\right\} \\ $$$${a}_{\mathrm{100}} =−\frac{\mathrm{2}}{\mathrm{3}}\left\{\mathrm{2}\left(−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{0}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{1}} }−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+...+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{99}} }\right)−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{100}} }\right\} \\ $$$${a}_{\mathrm{100}} =−\frac{\mathrm{2}}{\mathrm{3}}\left\{\mathrm{2}\left(−\frac{\mathrm{1}−\left(−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{100}} }{\mathrm{1}−\left(−\frac{\mathrm{1}}{\mathrm{3}}\right)}\right)−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{100}} }\right\} \\ $$$${a}_{\mathrm{100}} =−\frac{\mathrm{2}}{\mathrm{3}}\left\{−\frac{\mathrm{3}}{\mathrm{2}}\left[\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{100}} }\right]−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{100}} }\right\} \\ $$$${a}_{\mathrm{100}} =−\frac{\mathrm{2}}{\mathrm{3}}\left\{−\frac{\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}×\mathrm{3}^{\mathrm{100}} }\right\} \\ $$$$\Rightarrow{a}_{\mathrm{100}} =\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{101}} } \\ $$$$ \\ $$$${in}\:{general}\:{a}_{{n}} =\left(−\mathrm{1}\right)^{{n}} −\frac{\mathrm{1}}{\mathrm{3}^{{n}+\mathrm{1}} } \\ $$
Commented by mr W last updated on 17/Feb/19
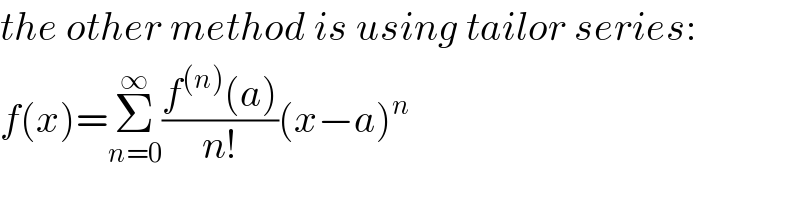
$${the}\:{other}\:{method}\:{is}\:{using}\:{tailor}\:{series}: \\ $$$${f}\left({x}\right)=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{f}^{\left({n}\right)} \left({a}\right)}{{n}!}\left({x}−{a}\right)^{{n}} \\ $$
Commented by mr W last updated on 17/Feb/19

$${this}\:{is}\:{the}\:{method}\:{i}\:{know},\:{only}\:{using} \\ $$$${geometric}\:{progression}. \\ $$$${please}\:{feedback}\:{if}\:{my}\:{answer}\:{is}\:{correct}. \\ $$
Commented by gunawan last updated on 17/Feb/19

$$\mathrm{Answer}\:\mathrm{is}\:\mathrm{correct}\:\mathrm{Sir} \\ $$$$\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much} \\ $$$$\mathrm{i}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{orther}\:\mathrm{solution} \\ $$
