
Question and Answers Forum
Question Number 55237 by peter frank last updated on 19/Feb/19
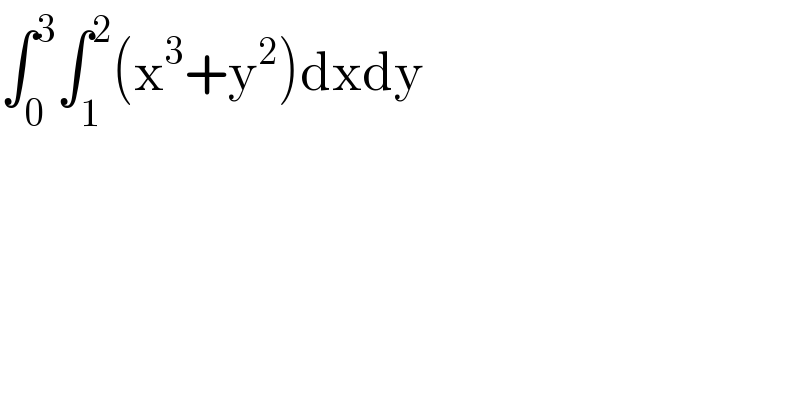
Commented by Abdo msup. last updated on 20/Feb/19
![I =∫_0 ^3 A(y)dy with A(y)=∫_1 ^2 (x^3 +y^2 )dx =∫_1 ^2 x^3 dx +y^2 ∫_1 ^2 dx =[(x^4 /4)]_1 ^2 +y^2 =(1/4)( 2^4 −1) +y^2 =((15)/4) +y^2 ⇒ I =∫_0 ^3 (((15)/4)+y^2 )dy =((45)/4) +[(1/3)y^3 ]_0 ^3 =((45)/4) +9 =((45+36)/4) =((81)/4)](Q55242.png)
Answered by kaivan.ahmadi last updated on 20/Feb/19
![∫_0 ^3 ((x^4 /4)+y^2 x]_1 ^2 )dy=∫_0 ^3 (4+2y^2 −(1/4)−y^2 )dy= ∫_0 ^3 (y^2 +((15)/4))dy=(y^3 /3)+((15)/4)y]_0 ^3 =9+((45)/4)=((81)/4)](Q55239.png)
| ||
Question and Answers Forum | ||
Question Number 55237 by peter frank last updated on 19/Feb/19 | ||
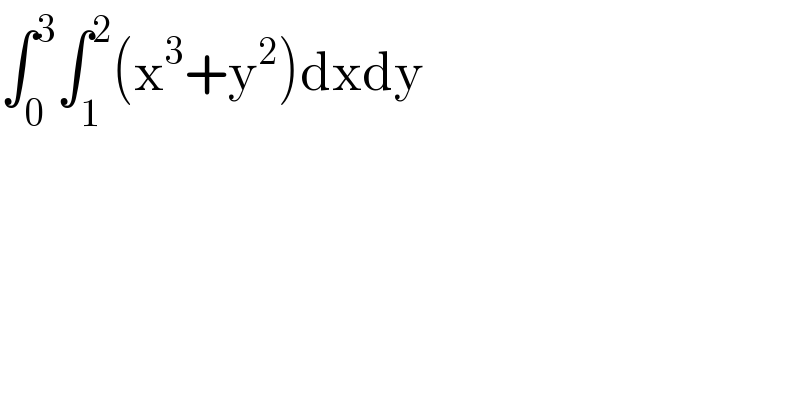 | ||
Commented by Abdo msup. last updated on 20/Feb/19 | ||
![I =∫_0 ^3 A(y)dy with A(y)=∫_1 ^2 (x^3 +y^2 )dx =∫_1 ^2 x^3 dx +y^2 ∫_1 ^2 dx =[(x^4 /4)]_1 ^2 +y^2 =(1/4)( 2^4 −1) +y^2 =((15)/4) +y^2 ⇒ I =∫_0 ^3 (((15)/4)+y^2 )dy =((45)/4) +[(1/3)y^3 ]_0 ^3 =((45)/4) +9 =((45+36)/4) =((81)/4)](Q55242.png) | ||
Answered by kaivan.ahmadi last updated on 20/Feb/19 | ||
![∫_0 ^3 ((x^4 /4)+y^2 x]_1 ^2 )dy=∫_0 ^3 (4+2y^2 −(1/4)−y^2 )dy= ∫_0 ^3 (y^2 +((15)/4))dy=(y^3 /3)+((15)/4)y]_0 ^3 =9+((45)/4)=((81)/4)](Q55239.png) | ||
| ||