Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 55310 by afachri last updated on 21/Feb/19

$$$$$$\int 3x\sqrt{3x^3+7}dx=....$$

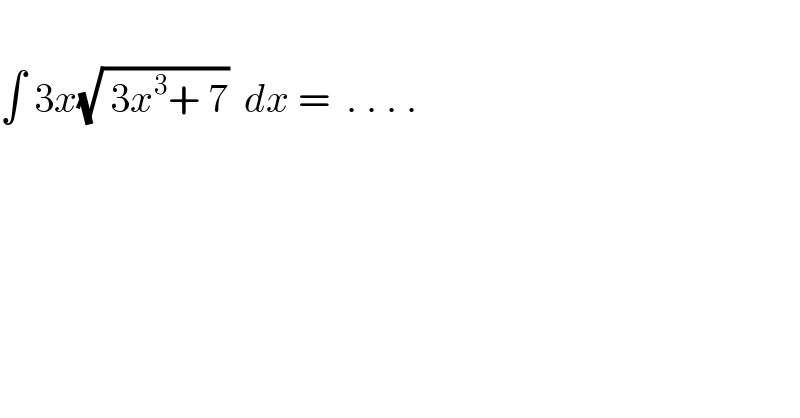
Commented by MJS last updated on 22/Feb/19

$$\mathrm{where}\mathrm{does}\mathrm{this}\mathrm{come}\mathrm{from}?$$$$\mathrm{I}\mathrm{tried}\mathrm{everything}\mathrm{I}\mathrm{know}\mathrm{but}\mathrm{it}\mathrm{seems}$$$$\mathrm{impossible}...\mathrm{of}\mathrm{course}3x^2\sqrt{3x^3+7}\mathrm{would}\mathrm{be}$$$$\mathrm{easy}$$

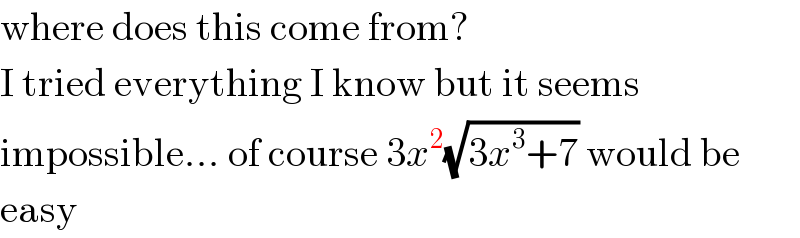
Answered by tanmay.chaudhury50@gmail.com last updated on 21/Feb/19

$$3x^3=7{tan}^2\theta \to x={\left(\frac{7{tan}^2\theta }{3}\right)}^{\frac{1}{3}}$$$$9x^{2}dx=14tan\theta {sec}^2\theta d\theta$$$$dx=\frac{14tan\theta {sec}^2\theta d\theta }{9{\left(\frac{7{tan}^2\theta }{3}\right)}^{\frac{2}{3}}}d\theta$$$$\int \frac{3{\left(\frac{7{tan}^2\theta }{3}\right)}^{\frac{1}{3}}\times \sqrt{7{tan}^2\theta +7}\times 14tan\theta {sec}^2\theta d\theta }{9{\left(\frac{7{tan}^2\theta }{3}\right)}^{\frac{2}{3}}}$$$$\frac{3}{9}\int \frac{\sqrt{7}sec\theta \times 14tan\theta \times {sec}^2\theta }{{\left(\frac{7}{3}\right)}^{\frac{2}{3}}\times {\left(tan\theta \right)}^{\frac{4}{3}}}d\theta$$$$\frac{1}{3}\times 14\sqrt{7}\times {\left(\frac{3}{7}\right)}^{\frac{2}{3}}\int \frac{{sec}^3\theta }{{\left(tan\theta \right)}^{\frac{1}{3}}}d\theta$$$$$$$$I=\int \frac{{sec}^3\theta }{{\left(tan\theta \right)}^{\frac{1}{3}}}d\theta$$$$sec\theta \int {sec}^2\theta \times \frac{1}{{\left(tan\theta \right)}^{\frac{1}{3}}}d\theta -\int [\frac{d}{d\theta }\left(sec\theta \right)\int \frac{{sec}^2\theta }{{\left(tan\theta \right)}^{\frac{1}{3}}}d\theta ]d\theta$$$$sec\theta \times \frac{{\left(tan\theta \right)}^{\frac{-1}{3}+1}}{\frac{2}{3}}-\int sec\theta tan\theta \times \frac{{\left(tan\theta \right)}^{\frac{2}{3}}}{\frac{2}{3}}d\theta$$$$\frac{3}{2}sec\theta {\left(tan\theta \right)}^{\frac{2}{3}}-\frac{3}{2}\int sec\theta tan\theta {({sec}^2\theta -1)}^{\frac{1}{3}}d\theta$$$$\frac{3}{2}sec\theta {\left(tan\theta \right)}^{\frac{3}{2}}-\frac{3}{2}\int {(a^2-1)}^{\frac{1}{3}}da$$$$curfewinheadquater...thatisbrain...wait...$$$$$$$$$$

Commented by afachri last updated on 21/Feb/19

$$\mathbf{it}\mathbf{is}\mathbf{hard},{\mathbf{isn}}^{\prime }\mathbf{t}\mathbf{it}\mathbf{Sir}??$$

Commented by afachri last updated on 21/Feb/19

$$\mathbf{oh}\mathbf{sir},\mathbf{i}\mathbf{think}\mathbf{my}\mathbf{mind}\mathbf{has}\mathbf{blown}.$$$$\mathbf{hehehe}...$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com