Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 55454 by maxmathsup by imad last updated on 24/Feb/19

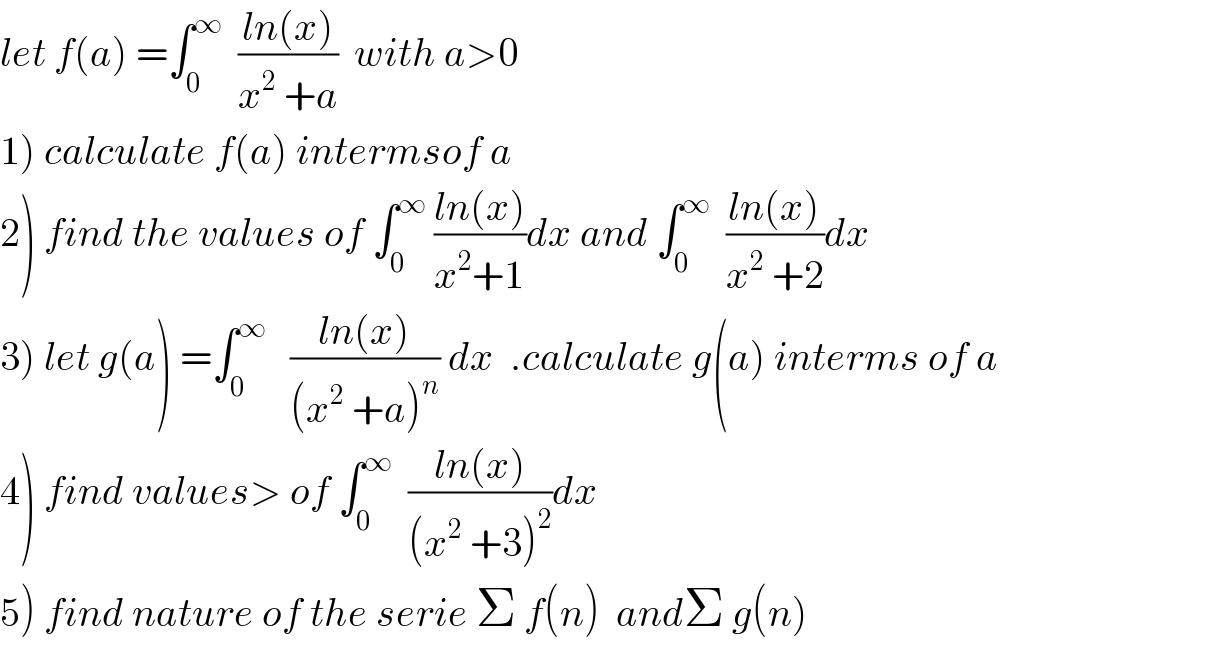
let f(a) =∫_0 ^∞ ((ln(x))/(x^2 +a)) with a>0 1) calculate f(a) intermsof a 2) find the values of ∫_0 ^∞ ((ln(x))/(x^2 +1))dx and ∫_0 ^∞ ((ln(x))/(x^2 +2))dx 3) let g(a) =∫_0 ^∞ ((ln(x))/((x^2 +a)^n )) dx .calculate g(a) interms of a 4) find values> of ∫_0 ^∞ ((ln(x))/((x^2 +3)^2 ))dx 5) find nature of the serie Σ f(n) andΣ g(n)

$${let}\:{f}\left({a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{ln}\left({x}\right)}{{x}^{\mathrm{2}} \:+{a}}\:\:{with}\:{a}>\mathrm{0} \\ $$ $$\left.\mathrm{1}\right)\:{calculate}\:{f}\left({a}\right)\:{intermsof}\:{a} \\ $$ $$\left.\mathrm{2}\right)\:{find}\:{the}\:{values}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{ln}\left({x}\right)}{{x}^{\mathrm{2}} +\mathrm{1}}{dx}\:{and}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{ln}\left({x}\right)}{{x}^{\mathrm{2}} \:+\mathrm{2}}{dx} \\ $$ $$\left.\mathrm{3}\right)\:{let}\:{g}\left({a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{ln}\left({x}\right)}{\left({x}^{\mathrm{2}} \:+{a}\right)^{{n}} }\:{dx}\:\:.{calculate}\:{g}\left({a}\right)\:{interms}\:{of}\:{a} \\ $$ $$\left.\mathrm{4}\right)\:{find}\:{values}>\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{ln}\left({x}\right)}{\left({x}^{\mathrm{2}} \:+\mathrm{3}\right)^{\mathrm{2}} }{dx} \\ $$ $$\left.\mathrm{5}\right)\:{find}\:{nature}\:{of}\:{the}\:{serie}\:\Sigma\:{f}\left({n}\right)\:\:{and}\Sigma\:{g}\left({n}\right)\: \\ $$

Commented bymaxmathsup by imad last updated on 24/Feb/19

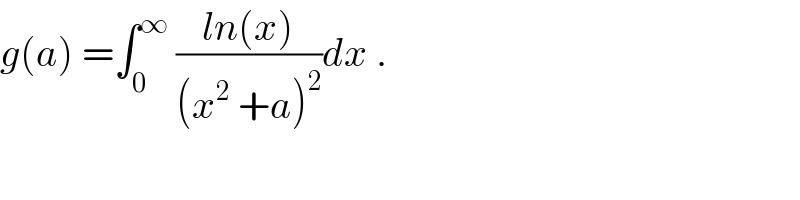
g(a) =∫_0 ^∞ ((ln(x))/((x^2 +a)^2 ))dx .

$${g}\left({a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{ln}\left({x}\right)}{\left({x}^{\mathrm{2}} \:+{a}\right)^{\mathrm{2}} }{dx}\:. \\ $$

Commented bymaxmathsup by imad last updated on 26/Feb/19

1) changement x =(√a)t give f(a) =∫_0 ^∞ ((ln((√a)t))/(a(t^2 +1))) (√a)dt =(1/(√a)) ∫_0 ^∞ ((ln((√a))+ln(t))/(1+t^2 ))dt =((ln((√(a))))/(√a))∫_0 ^∞ (dt/(1+t^2 )) +(1/(√a))∫_0 ^∞ ((ln(t))/(1+t^2 )) dt but chang.t =(1/u) drive to ∫_0 ^∞ ((ln(t))/(1+t^2 ))dt=0 ⇒ f(a) =(π/2) ((ln((√a)))/(√a)) ⇒ ★f(a) =(π/4) ((ln(a))/(√a)) ★ 2)we have ∫_0 ^∞ ((ln(x))/(x^2 +1))dx =f(1) =0 ∫_0 ^∞ ((ln(x))/(x^2 +2)) dx =f(2) =((πln(2))/(4(√2))) 3)we have f^′ (a) =−∫_0 ^∞ ((ln(x))/((x^2 +a)^2 )) dx =−g(a) ⇒g(a)=−f^′ (a) but f^′ (a) =(π/4) ((((√a)/a)−ln(a)(1/(2(√a))))/a) =(π/4) (((2a−aln(a))/(2a(√a)))/a) =(π/4) ((2−lna)/(2a(√a))) ⇒ ★g(a) =((π(ln(a)−2))/(8a(√a)))★ 4)∫_0 ^∞ ((ln(x))/((x^2 +3)^2 ))dx =g(3)=((π(ln3−2))/(24(√3)))

$$\left.\mathrm{1}\right)\:{changement}\:{x}\:=\sqrt{{a}}{t}\:{give}\:{f}\left({a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{ln}\left(\sqrt{{a}}{t}\right)}{{a}\left({t}^{\mathrm{2}} +\mathrm{1}\right)}\:\sqrt{{a}}{dt}\:=\frac{\mathrm{1}}{\sqrt{{a}}}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{ln}\left(\sqrt{{a}}\right)+{ln}\left({t}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$ $$=\frac{{ln}\left(\sqrt{\left.{a}\right)}\right.}{\sqrt{{a}}}\int_{\mathrm{0}} ^{\infty} \:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\sqrt{{a}}}\int_{\mathrm{0}} ^{\infty} \:\frac{{ln}\left({t}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt}\:\:{but}\:{chang}.{t}\:=\frac{\mathrm{1}}{{u}}\:{drive}\:{to}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{ln}\left({t}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}=\mathrm{0}\:\Rightarrow \\ $$ $${f}\left({a}\right)\:=\frac{\pi}{\mathrm{2}}\:\frac{{ln}\left(\sqrt{{a}}\right)}{\sqrt{{a}}}\:\Rightarrow\:\bigstar{f}\left({a}\right)\:=\frac{\pi}{\mathrm{4}}\:\frac{{ln}\left({a}\right)}{\sqrt{{a}}}\:\bigstar \\ $$ $$\left.\mathrm{2}\right){we}\:{have}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{ln}\left({x}\right)}{{x}^{\mathrm{2}} \:+\mathrm{1}}{dx}\:={f}\left(\mathrm{1}\right)\:=\mathrm{0} \\ $$ $$\int_{\mathrm{0}} ^{\infty} \:\frac{{ln}\left({x}\right)}{{x}^{\mathrm{2}} \:+\mathrm{2}}\:{dx}\:={f}\left(\mathrm{2}\right)\:=\frac{\pi{ln}\left(\mathrm{2}\right)}{\mathrm{4}\sqrt{\mathrm{2}}} \\ $$ $$\left.\mathrm{3}\right){we}\:{have}\:{f}^{'} \left({a}\right)\:=−\int_{\mathrm{0}} ^{\infty} \:\:\frac{{ln}\left({x}\right)}{\left({x}^{\mathrm{2}} \:+{a}\right)^{\mathrm{2}} }\:{dx}\:=−{g}\left({a}\right)\:\Rightarrow{g}\left({a}\right)=−{f}^{'} \left({a}\right) \\ $$ $${but}\:{f}^{'} \left({a}\right)\:=\frac{\pi}{\mathrm{4}}\:\frac{\frac{\sqrt{{a}}}{{a}}−{ln}\left({a}\right)\frac{\mathrm{1}}{\mathrm{2}\sqrt{{a}}}}{{a}}\:=\frac{\pi}{\mathrm{4}}\:\frac{\frac{\mathrm{2}{a}−{aln}\left({a}\right)}{\mathrm{2}{a}\sqrt{{a}}}}{{a}}\:=\frac{\pi}{\mathrm{4}}\:\frac{\mathrm{2}−{lna}}{\mathrm{2}{a}\sqrt{{a}}}\:\Rightarrow \\ $$ $$\bigstar{g}\left({a}\right)\:=\frac{\pi\left({ln}\left({a}\right)−\mathrm{2}\right)}{\mathrm{8}{a}\sqrt{{a}}}\bigstar \\ $$ $$\left.\mathrm{4}\right)\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{ln}\left({x}\right)}{\left({x}^{\mathrm{2}} \:+\mathrm{3}\right)^{\mathrm{2}} }{dx}\:={g}\left(\mathrm{3}\right)=\frac{\pi\left({ln}\mathrm{3}−\mathrm{2}\right)}{\mathrm{24}\sqrt{\mathrm{3}}} \\ $$

Commented bymaxmathsup by imad last updated on 26/Feb/19

5) we have Σ_(n≥1) f(n) =(π/4)Σ_(n≥1) ((ln(n))/(√n)) let ϕ(t)=((ln(t))/(√t)) ⇒ϕ^′ (t) =((((√t)/t)−ln(t)(1/(2(√t))))/t) =(((1/(√t))−((ln(t))/(2(√t))))/t) =((2−ln(t))/(2t(√t))) for t≥e^2 ⇒ln(t)≥2 ⇒ ϕ^′ (t)≤0 ⇒ ϕ is decreasing so Σ f(n) and ∫_e^2 ^(+∞) ((ln(x))/(√x)) dx have the same nature ∫_e^2 ^(+∞) ((ln(x))/(√x)) dx =_(x=t^2 ) ∫_e ^(+∞) ((2ln(t))/t) (2t)dt = 4∫_e ^(+∞) ln(t)dt =+∞ ⇒ Σ f(n) is divergent .

$$\left.\mathrm{5}\right)\:{we}\:{have}\:\sum_{{n}\geqslant\mathrm{1}} \:{f}\left({n}\right)\:=\frac{\pi}{\mathrm{4}}\sum_{{n}\geqslant\mathrm{1}} \:\:\:\frac{{ln}\left({n}\right)}{\sqrt{{n}}} \\ $$ $${let}\:\varphi\left({t}\right)=\frac{{ln}\left({t}\right)}{\sqrt{{t}}}\:\:\:\Rightarrow\varphi^{'} \left({t}\right)\:=\frac{\frac{\sqrt{{t}}}{{t}}−{ln}\left({t}\right)\frac{\mathrm{1}}{\mathrm{2}\sqrt{{t}}}}{{t}}\:=\frac{\frac{\mathrm{1}}{\sqrt{{t}}}−\frac{{ln}\left({t}\right)}{\mathrm{2}\sqrt{{t}}}}{{t}}\:=\frac{\mathrm{2}−{ln}\left({t}\right)}{\mathrm{2}{t}\sqrt{{t}}} \\ $$ $${for}\:{t}\geqslant{e}^{\mathrm{2}} \:\Rightarrow{ln}\left({t}\right)\geqslant\mathrm{2}\:\Rightarrow\:\varphi^{'} \left({t}\right)\leqslant\mathrm{0}\:\Rightarrow\:\varphi\:{is}\:{decreasing}\:\:{so}\:\Sigma\:{f}\left({n}\right)\:{and}\: \\ $$ $$\int_{{e}^{\mathrm{2}} } ^{+\infty} \:\frac{{ln}\left({x}\right)}{\sqrt{{x}}}\:{dx}\:{have}\:{the}\:{same}\:{nature}\: \\ $$ $$\int_{{e}^{\mathrm{2}} } ^{+\infty} \:\:\frac{{ln}\left({x}\right)}{\sqrt{{x}}}\:{dx}\:=_{{x}={t}^{\mathrm{2}} } \:\:\:\:\:\int_{{e}} ^{+\infty} \:\:\frac{\mathrm{2}{ln}\left({t}\right)}{{t}}\:\left(\mathrm{2}{t}\right){dt}\:=\:\mathrm{4}\int_{{e}} ^{+\infty} {ln}\left({t}\right){dt}\:=+\infty\:\Rightarrow \\ $$ $$\Sigma\:{f}\left({n}\right)\:{is}\:{divergent}\:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com