
Question and Answers Forum
Question Number 55457 by maxmathsup by imad last updated on 24/Feb/19
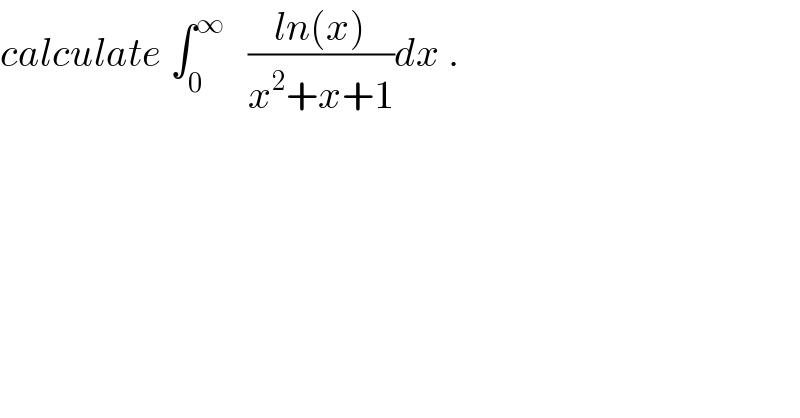
Commented by maxmathsup by imad last updated on 05/Mar/19
![let I =∫_0 ^∞ ((ln(x))/(x^2 +x+1))dx ⇒I =∫_0 ^∞ ((lnx)/((x+(1/2))^2 +(3/4)))dx =_(x+(1/2)=((√3)/2)t) ∫_(1/(√3)) ^(+∞) ((ln(((√3)/2)t−(1/2)))/((3/4)(1+t^2 ))) ((√3)/2)dt =(4/3) ((√3)/2) ∫_(1/(√3)) ^(+∞) ((ln(((√3)/2)t−(1/2)))/(1+t^2 ))dt =(2/(√3)) ∫_(1/(√3)) ^(+∞) ((ln(((√3)/2)t−(1/2)))/(t^2 +1))dt ⇒ I =(2/(√3)) ∫_(1/(√3)) ^(+∞) ((ln(((√3)/2)x−(1/2)))/(x^2 +1))dx let f(t) =∫_(1/(√3)) ^(+∞) ((ln(tx−1))/(x^2 +1))dx ⇒f^′ (t) =∫_(1/(√3)) ^(+∞) (x/((tx−1)(x^2 +1)))dx let decompise F(x) =(x/((tx−1)(x^2 +1))) ⇒F(x)=(a/(tx−1)) +((bx +c)/(x^2 +1)) a =lim_(x→(1/t)) (tx−1)F(x) =(1/(t((1/t^2 ) +1))) =(1/(t+(1/t))) =(t/(t^2 +1)) lim_(x→+∞) xF(x)=(a/t) +b =0 ⇒b =−(a/t) =−(1/(t^2 +1)) ⇒ F(x) =(t/((t^2 +1)(tx−1))) +((−(1/(t^2 +1))x+c)/(x^2 +1)) F(0) =0 =−(t/(t^2 +1)) +c ⇒c =(t/(t^2 +1)) ⇒ F(x) =(t/((t^2 +1)(tx−1))) +(1/(t^2 +1)) ((−x+t)/(x^2 +1)) ⇒ ∫ F(x)dx =(1/(t^2 +1))ln∣tx−1∣−(1/(2(t^2 +1)))ln(x^2 +1) +(t/(t^2 +1)) arctan(x) +c ⇒ ∫_(1/(√3)) ^(+∞) F(x)dx =(1/(t^2 +1))[ln∣((tx−1)/(√(x^2 +1)))∣]_(1/(√3)) ^(+∞) +(t/(t^2 +1))[arctant]_(1/(√3)) ^(+∞) =(1/(t^2 +1)){ln∣t∣−ln∣(((t/(√3))−1)/(2/(√3)))∣} +(t/(t^2 +1)){(π/2) −(π/6)} =(1/(t^2 +1)){ln∣t∣−ln∣((t−(√3))/2)∣} +((πt)/(3(t^2 +1))) =f^′ (t) ⇒ f(t) =∫ ((ln∣t∣)/(t^2 +1))dt−∫ ((ln∣t−(√3))−ln(2))/(t^2 +1)) dt +(π/6)ln(t^2 +1) +C =∫ ((ln∣t∣)/(t^2 +1))dt −∫((ln∣t−(√3)∣)/(t^2 +1))dt+ln(2)arctant +C ....be continued....](Q55896.png)
Commented by Abdo msup. last updated on 05/Mar/19
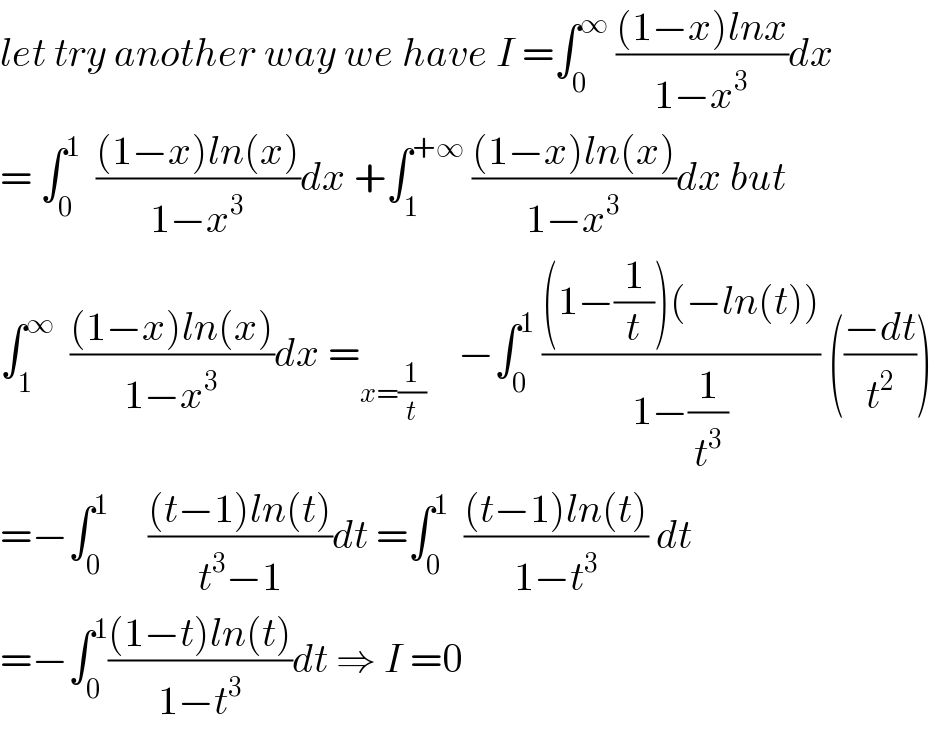
| ||
Question and Answers Forum | ||
Question Number 55457 by maxmathsup by imad last updated on 24/Feb/19 | ||
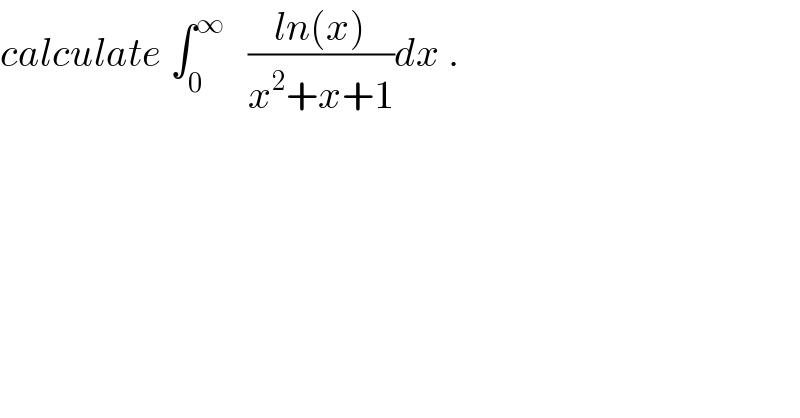 | ||
Commented by maxmathsup by imad last updated on 05/Mar/19 | ||
![let I =∫_0 ^∞ ((ln(x))/(x^2 +x+1))dx ⇒I =∫_0 ^∞ ((lnx)/((x+(1/2))^2 +(3/4)))dx =_(x+(1/2)=((√3)/2)t) ∫_(1/(√3)) ^(+∞) ((ln(((√3)/2)t−(1/2)))/((3/4)(1+t^2 ))) ((√3)/2)dt =(4/3) ((√3)/2) ∫_(1/(√3)) ^(+∞) ((ln(((√3)/2)t−(1/2)))/(1+t^2 ))dt =(2/(√3)) ∫_(1/(√3)) ^(+∞) ((ln(((√3)/2)t−(1/2)))/(t^2 +1))dt ⇒ I =(2/(√3)) ∫_(1/(√3)) ^(+∞) ((ln(((√3)/2)x−(1/2)))/(x^2 +1))dx let f(t) =∫_(1/(√3)) ^(+∞) ((ln(tx−1))/(x^2 +1))dx ⇒f^′ (t) =∫_(1/(√3)) ^(+∞) (x/((tx−1)(x^2 +1)))dx let decompise F(x) =(x/((tx−1)(x^2 +1))) ⇒F(x)=(a/(tx−1)) +((bx +c)/(x^2 +1)) a =lim_(x→(1/t)) (tx−1)F(x) =(1/(t((1/t^2 ) +1))) =(1/(t+(1/t))) =(t/(t^2 +1)) lim_(x→+∞) xF(x)=(a/t) +b =0 ⇒b =−(a/t) =−(1/(t^2 +1)) ⇒ F(x) =(t/((t^2 +1)(tx−1))) +((−(1/(t^2 +1))x+c)/(x^2 +1)) F(0) =0 =−(t/(t^2 +1)) +c ⇒c =(t/(t^2 +1)) ⇒ F(x) =(t/((t^2 +1)(tx−1))) +(1/(t^2 +1)) ((−x+t)/(x^2 +1)) ⇒ ∫ F(x)dx =(1/(t^2 +1))ln∣tx−1∣−(1/(2(t^2 +1)))ln(x^2 +1) +(t/(t^2 +1)) arctan(x) +c ⇒ ∫_(1/(√3)) ^(+∞) F(x)dx =(1/(t^2 +1))[ln∣((tx−1)/(√(x^2 +1)))∣]_(1/(√3)) ^(+∞) +(t/(t^2 +1))[arctant]_(1/(√3)) ^(+∞) =(1/(t^2 +1)){ln∣t∣−ln∣(((t/(√3))−1)/(2/(√3)))∣} +(t/(t^2 +1)){(π/2) −(π/6)} =(1/(t^2 +1)){ln∣t∣−ln∣((t−(√3))/2)∣} +((πt)/(3(t^2 +1))) =f^′ (t) ⇒ f(t) =∫ ((ln∣t∣)/(t^2 +1))dt−∫ ((ln∣t−(√3))−ln(2))/(t^2 +1)) dt +(π/6)ln(t^2 +1) +C =∫ ((ln∣t∣)/(t^2 +1))dt −∫((ln∣t−(√3)∣)/(t^2 +1))dt+ln(2)arctant +C ....be continued....](Q55896.png) | ||
Commented by Abdo msup. last updated on 05/Mar/19 | ||
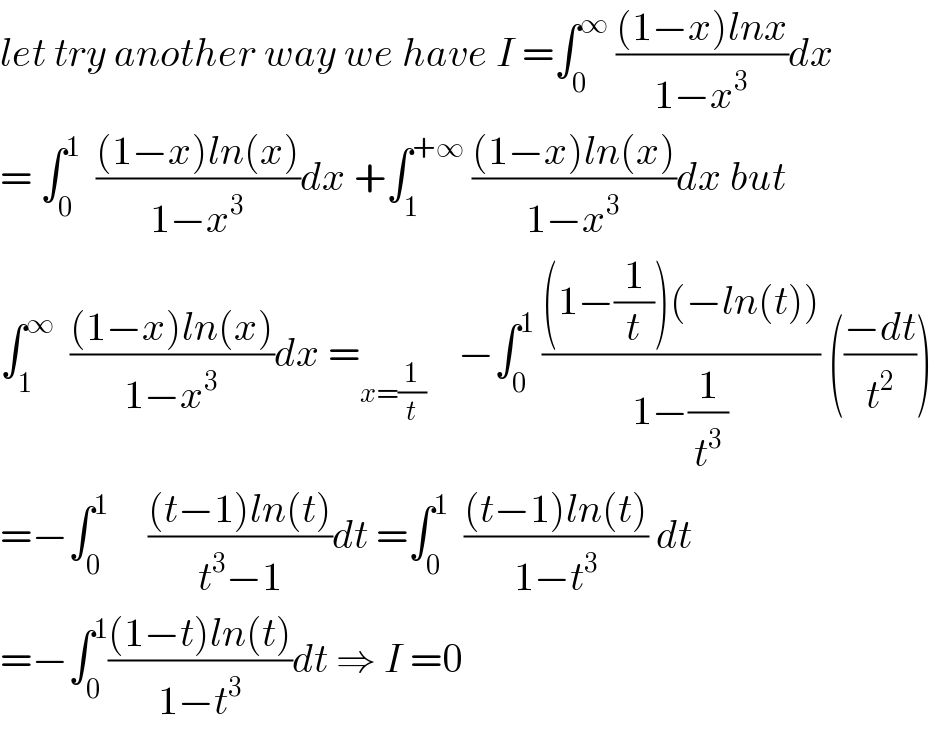 | ||