Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 55597 by ajfour last updated on 27/Feb/19

(d^2 y/dx^2 )+6y((dy/dx))^2 =0 Please solve the differential eq.

$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }+\mathrm{6}{y}\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${Please}\:{solve}\:{the}\:{differential}\:{eq}. \\ $$

Answered by mr W last updated on 27/Feb/19

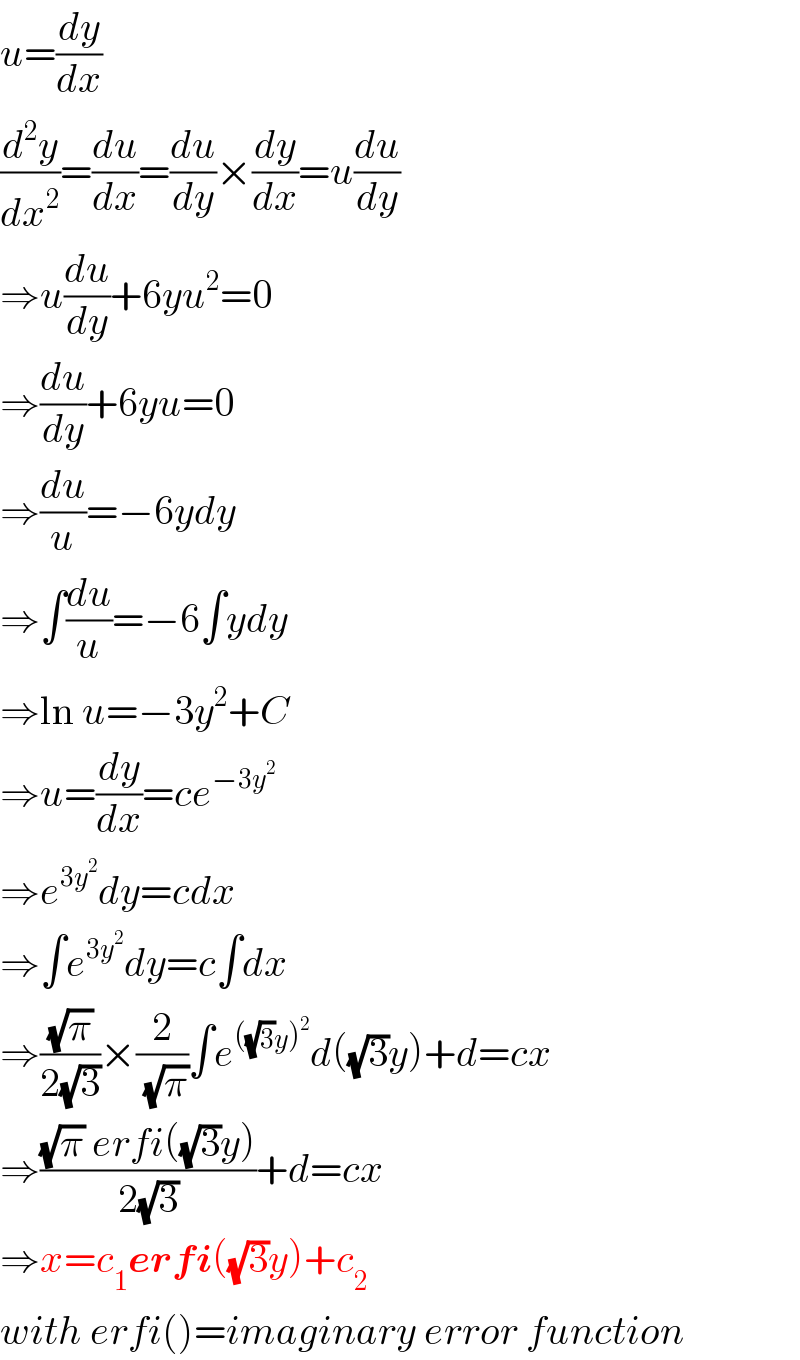
u=(dy/dx) (d^2 y/dx^2 )=(du/dx)=(du/dy)×(dy/dx)=u(du/dy) ⇒u(du/dy)+6yu^2 =0 ⇒(du/dy)+6yu=0 ⇒(du/u)=−6ydy ⇒∫(du/u)=−6∫ydy ⇒ln u=−3y^2 +C ⇒u=(dy/dx)=ce^(−3y^2 ) ⇒e^(3y^2 ) dy=cdx ⇒∫e^(3y^2 ) dy=c∫dx ⇒((√π)/(2(√3)))×(2/(√π))∫e^(((√3)y)^2 ) d((√3)y)+d=cx ⇒(((√π) erfi((√3)y))/(2(√3)))+d=cx ⇒x=c_1 erfi((√3)y)+c_2 with erfi()=imaginary error function

$${u}=\frac{{dy}}{{dx}} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{{du}}{{dx}}=\frac{{du}}{{dy}}×\frac{{dy}}{{dx}}={u}\frac{{du}}{{dy}} \\ $$$$\Rightarrow{u}\frac{{du}}{{dy}}+\mathrm{6}{yu}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\frac{{du}}{{dy}}+\mathrm{6}{yu}=\mathrm{0} \\ $$$$\Rightarrow\frac{{du}}{{u}}=−\mathrm{6}{ydy} \\ $$$$\Rightarrow\int\frac{{du}}{{u}}=−\mathrm{6}\int{ydy} \\ $$$$\Rightarrow\mathrm{ln}\:{u}=−\mathrm{3}{y}^{\mathrm{2}} +{C} \\ $$$$\Rightarrow{u}=\frac{{dy}}{{dx}}={ce}^{−\mathrm{3}{y}^{\mathrm{2}} } \\ $$$$\Rightarrow{e}^{\mathrm{3}{y}^{\mathrm{2}} } {dy}={cdx} \\ $$$$\Rightarrow\int{e}^{\mathrm{3}{y}^{\mathrm{2}} } {dy}={c}\int{dx} \\ $$$$\Rightarrow\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{\mathrm{3}}}×\frac{\mathrm{2}}{\sqrt{\pi}}\int{e}^{\left(\sqrt{\mathrm{3}}{y}\right)^{\mathrm{2}} } {d}\left(\sqrt{\mathrm{3}}{y}\right)+{d}={cx} \\ $$$$\Rightarrow\frac{\sqrt{\pi}\:{erfi}\left(\sqrt{\mathrm{3}}{y}\right)}{\mathrm{2}\sqrt{\mathrm{3}}}+{d}={cx} \\ $$$$\Rightarrow{x}={c}_{\mathrm{1}} \boldsymbol{{erfi}}\left(\sqrt{\mathrm{3}}{y}\right)+{c}_{\mathrm{2}} \\ $$$${with}\:{erfi}\left(\right)={imaginary}\:{error}\:{function} \\ $$

Commented by mr W last updated on 27/Feb/19

Commented by mr W last updated on 27/Feb/19

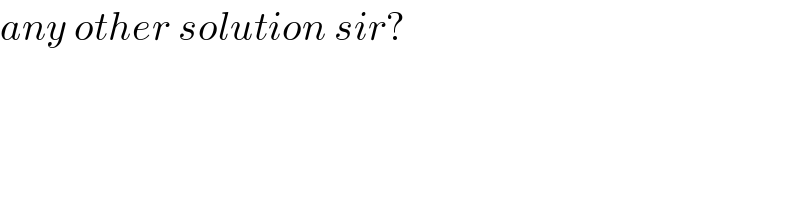
any other solution sir?

$${any}\:{other}\:{solution}\:{sir}? \\ $$

Commented by ajfour last updated on 27/Feb/19

Thank you Sir, goes beyond my expectation. if y=x^3 +px+q and if i swap x with y, x=y^3 +py+q Then 1=(3y^2 +p)(dy/dx) ...(i) 0=6y(dy/dx)+(3y^2 +p)(d^2 y/dx^2 ) using (i) 6y(dy/dx)+((((d^2 y/dx^2 )))/(((dy/dx)))) = 0 ⇒ (d^2 y/dx^2 )+6y((dy/dx))^2 =0 Its this way that i got the question Sir.

$${Thank}\:{you}\:{Sir},\:{goes}\:{beyond}\:{my} \\ $$$${expectation}. \\ $$$$\:\:\:\:\:{if}\:\:\:\:{y}={x}^{\mathrm{3}} +{px}+{q} \\ $$$${and}\:{if}\:{i}\:{swap}\:{x}\:{with}\:{y}, \\ $$$$\:\:\:{x}={y}^{\mathrm{3}} +{py}+{q} \\ $$$${Then}\:\:\:\:\mathrm{1}=\left(\mathrm{3}{y}^{\mathrm{2}} +{p}\right)\frac{{dy}}{{dx}}\:\:\:\:\:...\left({i}\right) \\ $$$$\:\:\:\mathrm{0}=\mathrm{6}{y}\frac{{dy}}{{dx}}+\left(\mathrm{3}{y}^{\mathrm{2}} +{p}\right)\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} } \\ $$$${using}\:\left({i}\right) \\ $$$$\:\:\:\:\:\mathrm{6}{y}\frac{{dy}}{{dx}}+\frac{\left(\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\right)}{\left(\frac{{dy}}{{dx}}\right)}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\:\:\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }+\mathrm{6}{y}\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${Its}\:{this}\:{way}\:{that}\:{i}\:{got}\:{the}\:{question} \\ $$$${Sir}. \\ $$

Commented by ajfour last updated on 27/Feb/19

knowing then that other solution is y^3 +py+q = x only we need to write y in terms of x. let y=u+v (u+v)^3 +p(u+v)+q=x u^3 +v^3 +(u+v)[3uv+p]=x−q let uv=−(p/3) ⇒ (uv)^3 =−(p^3 /(27)) ⇒ u^3 +v^3 =x−q ⇒ u^3 , v^3 are roots of z^2 −(x−q)z−(p^3 /(27)) =0 u^3 , v^3 = ((x−q)/2)±(√((((x−q)/2))^2 +(p^3 /(27)))) hence our y(x) can even be y=[((x−q)/2)+(√((((x−q)/2))^2 +(p^3 /(27)))) ]^(1/3) +[((x−q)/2)−(√((((x−q)/2))^2 +(p^3 /(27)))) ]^(1/3) p, q being the arbitrary constants. (∵_⌣ ) Congratulations Sir, its you who found the new cubic formula.

$${knowing}\:{then}\:{that}\:{other}\:{solution} \\ $$$${is}\:\:\:\:\:\:{y}^{\mathrm{3}} +{py}+{q}\:=\:{x} \\ $$$${only}\:{we}\:{need}\:{to}\:{write}\:{y}\:{in}\:{terms} \\ $$$${of}\:{x}. \\ $$$$\:\:\:\:\:\:\:\:\:\:{let}\:\:\:{y}={u}+{v} \\ $$$$\:\:\:\left({u}+{v}\right)^{\mathrm{3}} +{p}\left({u}+{v}\right)+{q}={x} \\ $$$$\:\:\:{u}^{\mathrm{3}} +{v}^{\mathrm{3}} +\left({u}+{v}\right)\left[\mathrm{3}{uv}+{p}\right]={x}−{q} \\ $$$$\:\:\:\:{let}\:\:\:{uv}=−\frac{{p}}{\mathrm{3}}\:\:\:\Rightarrow\:\:\left({uv}\right)^{\mathrm{3}} =−\frac{{p}^{\mathrm{3}} }{\mathrm{27}} \\ $$$$\Rightarrow\:\:\:\:{u}^{\mathrm{3}} +{v}^{\mathrm{3}} \:={x}−{q} \\ $$$$\Rightarrow\:\:{u}^{\mathrm{3}} ,\:{v}^{\mathrm{3}} \:\:{are}\:{roots}\:{of} \\ $$$$\:\:\:\:\:\:{z}^{\mathrm{2}} −\left({x}−{q}\right){z}−\frac{{p}^{\mathrm{3}} }{\mathrm{27}}\:=\mathrm{0} \\ $$$$\:\:{u}^{\mathrm{3}} ,\:{v}^{\mathrm{3}} \:=\:\frac{{x}−{q}}{\mathrm{2}}\pm\sqrt{\left(\frac{{x}−{q}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{{p}^{\mathrm{3}} }{\mathrm{27}}} \\ $$$$\:\:\:{hence}\:{our}\:{y}\left({x}\right)\:{can}\:{even}\:{be} \\ $$$$\:\:\:\:{y}=\left[\frac{{x}−{q}}{\mathrm{2}}+\sqrt{\left(\frac{{x}−{q}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{{p}^{\mathrm{3}} }{\mathrm{27}}}\:\right]^{\mathrm{1}/\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:+\left[\frac{{x}−{q}}{\mathrm{2}}−\sqrt{\left(\frac{{x}−{q}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{{p}^{\mathrm{3}} }{\mathrm{27}}}\:\right]^{\mathrm{1}/\mathrm{3}} \\ $$$${p},\:{q}\:{being}\:{the}\:{arbitrary}\:{constants}. \\ $$$$\:\:\:\:\:\:\:\left(\underset{\smallsmile} {\because}\right)\:\:{Congratulations}\:{Sir}, \\ $$$${its}\:{you}\:{who}\:{found}\:{the}\:{new}\:{cubic} \\ $$$${formula}. \\ $$

Commented by mr W last updated on 27/Feb/19

i need some time to catch you fully.

$${i}\:{need}\:{some}\:{time}\:{to}\:{catch}\:{you}\:{fully}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com