Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 5561 by Rasheed Soomro last updated on 20/May/16

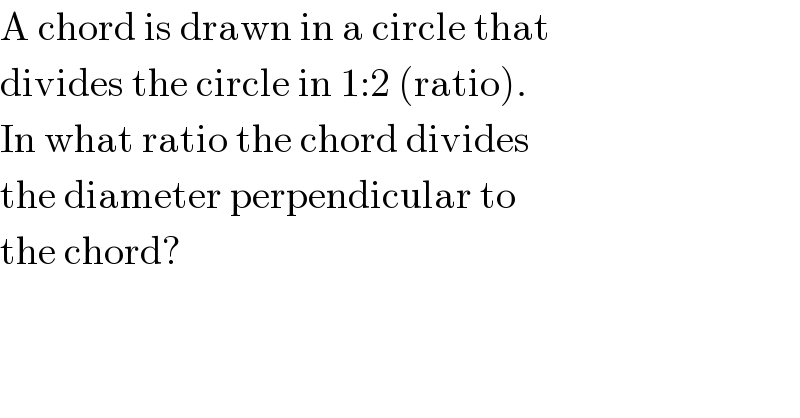
A chord is drawn in a circle that divides the circle in 1:2 (ratio). In what ratio the chord divides the diameter perpendicular to the chord?

$$\mathrm{A}\:\mathrm{chord}\:\mathrm{is}\:\mathrm{drawn}\:\mathrm{in}\:\mathrm{a}\:\mathrm{circle}\:\mathrm{that} \\ $$$$\mathrm{divides}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{in}\:\mathrm{1}:\mathrm{2}\:\left(\mathrm{ratio}\right). \\ $$$$\mathrm{In}\:\mathrm{what}\:\mathrm{ratio}\:\mathrm{the}\:\mathrm{chord}\:\mathrm{divides} \\ $$$$\mathrm{the}\:\mathrm{diameter}\:\mathrm{perpendicular}\:\mathrm{to} \\ $$$$\mathrm{the}\:\mathrm{chord}? \\ $$

Commented by Rasheed Soomro last updated on 20/May/16

Commented by Rasheed Soomro last updated on 20/May/16

Given:Area SegmentBEC:AreaSegmentBDC=1:2 ED⊥BC Required:EF:FD=?

$$\mathrm{Given}:{Area}\:\mathrm{SegmentBEC}:{Area}\mathrm{SegmentBDC}=\mathrm{1}:\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{ED}\bot\mathrm{BC} \\ $$$$\mathrm{Required}:\mathrm{EF}:\mathrm{FD}=? \\ $$

Answered by Rasheed Soomro last updated on 21/May/16

Commented by Rasheed Soomro last updated on 22/May/16

Seg=Segment, Sec=Sector AreaSegBDC=AreaSecBDC−▲ABC Let r is radius of the circle and Central angle of secBDC=α rad. AreaSecBDC=(1/2)r^2 α ▲ABC=(1/2)r^2 sin α AreaSegBDC=(1/2)r^2 α−(1/2)r^2 sin α =(1/2)r^2 [α−sin α] AreaSegBEC=π r^2 −AreaSegBDC =π r^2 −((1/2))r^2 [α−sin α] =r^2 (π−(1/2)[α−sin α]) AreaSegBDC : AreaSegBEC=1 : 2 (((1/2)r^2 [α−sin α])/(r^2 (π−(1/2)[α−sin α])))=(1/2) (((1/2)[α−sin α])/(π−(1/2)[α−sin α]))=(1/2) α−sin α=π−(1/2)[α−sin α] 2α−2 sin α=2π−α+sin α 3α−3 sin α=2π α−sin α=(2/3)π Now in △AFB ∠AFB=π/2 rad ∠FAB=(α/2) rad cos(∠FAB)=((AF)/(AB))=((AF)/r) AF=r cos(α/2) DF=k=r−AF=r−r cos(α/2)=r(1−cos(α/2)) FE=2r−k=2r−r(1−cos(α/2))=r(1+cos(α/2)) ((DF)/(FE))=((r(1−cos(α/2)))/(r(1+cos(α/2))))=((1−cos(α/2))/(1+cos(α/2))) Required ratio (((DF)/(FE)))=((1−cos(α/2))/(1+cos(α/2))) ,where α is such that α−sin α=(2/3)π

$$\mathrm{Seg}=\mathrm{Segment},\:\mathrm{Sec}=\mathrm{Sector} \\ $$$$\mathrm{AreaSegBDC}=\mathrm{AreaSecBDC}−\blacktriangle\mathrm{ABC} \\ $$$$\:\:\:\:\:\:\:\mathrm{Let}\:\mathrm{r}\:\mathrm{is}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{and} \\ $$$$\:\:\:\:\:\:\:\mathrm{Central}\:\mathrm{angle}\:\mathrm{of}\:\mathrm{secBDC}=\alpha\:\mathrm{rad}. \\ $$$$\:\:\:\:\:\:\:\mathrm{AreaSecBDC}=\left(\mathrm{1}/\mathrm{2}\right)\mathrm{r}^{\mathrm{2}} \alpha \\ $$$$\:\:\:\:\:\:\:\:\blacktriangle\mathrm{ABC}=\left(\mathrm{1}/\mathrm{2}\right)\mathrm{r}^{\mathrm{2}} \mathrm{sin}\:\alpha \\ $$$$\mathrm{AreaSegBDC}=\left(\mathrm{1}/\mathrm{2}\right)\mathrm{r}^{\mathrm{2}} \alpha−\left(\mathrm{1}/\mathrm{2}\right)\mathrm{r}^{\mathrm{2}} \mathrm{sin}\:\alpha \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{1}/\mathrm{2}\right)\mathrm{r}^{\mathrm{2}} \left[\alpha−\mathrm{sin}\:\alpha\right] \\ $$$$\mathrm{AreaSegBEC}=\pi\:\mathrm{r}^{\mathrm{2}} −\mathrm{AreaSegBDC} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\pi\:\mathrm{r}^{\mathrm{2}} −\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\mathrm{r}^{\mathrm{2}} \left[\alpha−\mathrm{sin}\:\alpha\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{r}^{\mathrm{2}} \left(\pi−\frac{\mathrm{1}}{\mathrm{2}}\left[\alpha−\mathrm{sin}\:\alpha\right]\right) \\ $$$$\mathrm{AreaSegBDC}\::\:\mathrm{AreaSegBEC}=\mathrm{1}\::\:\mathrm{2} \\ $$$$\frac{\left(\mathrm{1}/\mathrm{2}\right)\mathrm{r}^{\mathrm{2}} \left[\alpha−\mathrm{sin}\:\alpha\right]}{\mathrm{r}^{\mathrm{2}} \left(\pi−\left(\mathrm{1}/\mathrm{2}\right)\left[\alpha−\mathrm{sin}\:\alpha\right]\right)}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{\left(\mathrm{1}/\mathrm{2}\right)\left[\alpha−\mathrm{sin}\:\alpha\right]}{\pi−\left(\mathrm{1}/\mathrm{2}\right)\left[\alpha−\mathrm{sin}\:\alpha\right]}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\alpha−\mathrm{sin}\:\alpha=\pi−\left(\mathrm{1}/\mathrm{2}\right)\left[\alpha−\mathrm{sin}\:\alpha\right] \\ $$$$\mathrm{2}\alpha−\mathrm{2}\:\mathrm{sin}\:\alpha=\mathrm{2}\pi−\alpha+\mathrm{sin}\:\alpha \\ $$$$\mathrm{3}\alpha−\mathrm{3}\:\mathrm{sin}\:\alpha=\mathrm{2}\pi \\ $$$$\alpha−\mathrm{sin}\:\alpha=\frac{\mathrm{2}}{\mathrm{3}}\pi \\ $$$$\mathrm{Now}\:\mathrm{in}\:\bigtriangleup\mathrm{AFB} \\ $$$$\angle\mathrm{AFB}=\pi/\mathrm{2}\:\:\mathrm{rad} \\ $$$$\angle\mathrm{FAB}=\frac{\alpha}{\mathrm{2}}\:\mathrm{rad} \\ $$$$\mathrm{cos}\left(\angle\mathrm{FAB}\right)=\frac{\mathrm{AF}}{\mathrm{AB}}=\frac{\mathrm{AF}}{\mathrm{r}} \\ $$$$\mathrm{AF}=\mathrm{r}\:\mathrm{cos}\left(\alpha/\mathrm{2}\right) \\ $$$$\mathrm{DF}=\mathrm{k}=\mathrm{r}−\mathrm{AF}=\mathrm{r}−\mathrm{r}\:\mathrm{cos}\left(\alpha/\mathrm{2}\right)=\mathrm{r}\left(\mathrm{1}−\mathrm{cos}\frac{\alpha}{\mathrm{2}}\right) \\ $$$$\mathrm{FE}=\mathrm{2r}−\mathrm{k}=\mathrm{2r}−\mathrm{r}\left(\mathrm{1}−\mathrm{cos}\frac{\alpha}{\mathrm{2}}\right)=\mathrm{r}\left(\mathrm{1}+\mathrm{cos}\frac{\alpha}{\mathrm{2}}\right) \\ $$$$\frac{\mathrm{DF}}{\mathrm{FE}}=\frac{\mathrm{r}\left(\mathrm{1}−\mathrm{cos}\frac{\alpha}{\mathrm{2}}\right)}{\mathrm{r}\left(\mathrm{1}+\mathrm{cos}\frac{\alpha}{\mathrm{2}}\right)}=\frac{\mathrm{1}−\mathrm{cos}\frac{\alpha}{\mathrm{2}}}{\mathrm{1}+\mathrm{cos}\frac{\alpha}{\mathrm{2}}} \\ $$$$\mathrm{Required}\:\mathrm{ratio}\:\left(\frac{\mathrm{DF}}{\mathrm{FE}}\right)=\frac{\mathrm{1}−\mathrm{cos}\frac{\alpha}{\mathrm{2}}}{\mathrm{1}+\mathrm{cos}\frac{\alpha}{\mathrm{2}}}\:,\mathrm{where}\:\alpha\:\mathrm{is} \\ $$$$\mathrm{such}\:\mathrm{that}\:\:\:\:\alpha−\mathrm{sin}\:\alpha=\frac{\mathrm{2}}{\mathrm{3}}\pi \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com