Question and Answers Forum

All Questions      Topic List

Logarithms Questions

Previous in All Question      Next in All Question      

Previous in Logarithms      Next in Logarithms      

Question Number 5569 by Rasheed Soomro last updated on 20/May/16

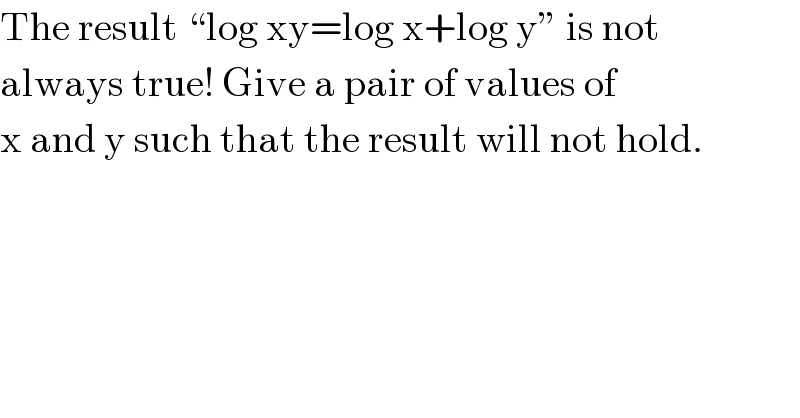
The result “log xy=log x+log y” is not always true! Give a pair of values of x and y such that the result will not hold.

$$\mathrm{The}\:\mathrm{result}\:``\mathrm{log}\:\mathrm{xy}=\mathrm{log}\:\mathrm{x}+\mathrm{log}\:\mathrm{y}''\:\mathrm{is}\:\mathrm{not} \\ $$$$\mathrm{always}\:\mathrm{true}!\:\mathrm{Give}\:\mathrm{a}\:\mathrm{pair}\:\mathrm{of}\:\mathrm{values}\:\mathrm{of} \\ $$$$\mathrm{x}\:\mathrm{and}\:\mathrm{y}\:\mathrm{such}\:\mathrm{that}\:\mathrm{the}\:\mathrm{result}\:\mathrm{will}\:\mathrm{not}\:\mathrm{hold}. \\ $$

Commented by Yozzii last updated on 20/May/16

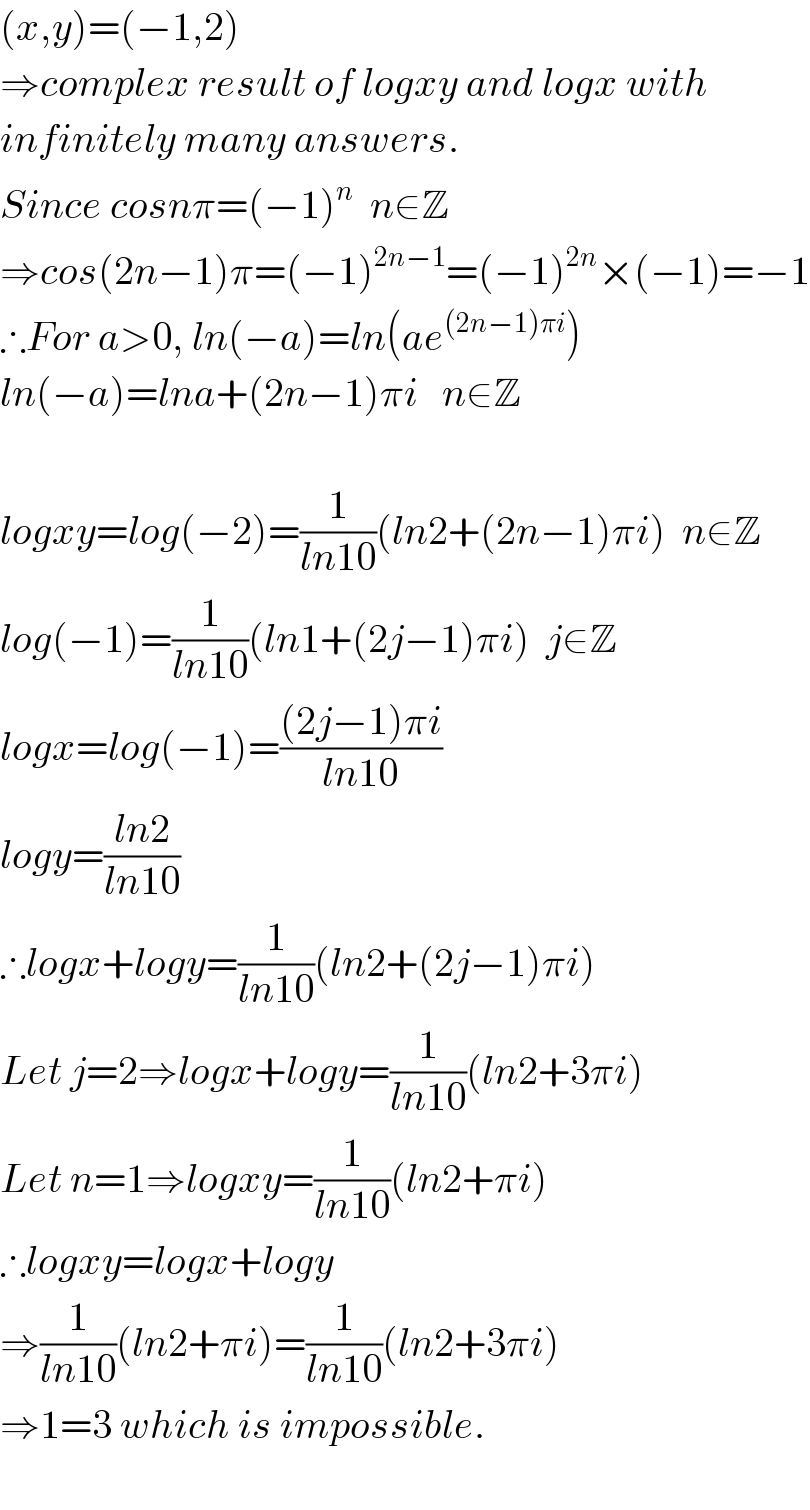
(x,y)=(−1,2) ⇒complex result of logxy and logx with infinitely many answers. Since cosnπ=(−1)^n n∈Z ⇒cos(2n−1)π=(−1)^(2n−1) =(−1)^(2n) ×(−1)=−1 ∴For a>0, ln(−a)=ln(ae^((2n−1)πi) ) ln(−a)=lna+(2n−1)πi n∈Z logxy=log(−2)=(1/(ln10))(ln2+(2n−1)πi) n∈Z log(−1)=(1/(ln10))(ln1+(2j−1)πi) j∈Z logx=log(−1)=(((2j−1)πi)/(ln10)) logy=((ln2)/(ln10)) ∴logx+logy=(1/(ln10))(ln2+(2j−1)πi) Let j=2⇒logx+logy=(1/(ln10))(ln2+3πi) Let n=1⇒logxy=(1/(ln10))(ln2+πi) ∴logxy=logx+logy ⇒(1/(ln10))(ln2+πi)=(1/(ln10))(ln2+3πi) ⇒1=3 which is impossible.

$$\left({x},{y}\right)=\left(−\mathrm{1},\mathrm{2}\right) \\ $$$$\Rightarrow{complex}\:{result}\:{of}\:{logxy}\:{and}\:{logx}\:{with} \\ $$$${infinitely}\:{many}\:{answers}. \\ $$$${Since}\:{cosn}\pi=\left(−\mathrm{1}\right)^{{n}} \:\:{n}\in\mathbb{Z} \\ $$$$\Rightarrow{cos}\left(\mathrm{2}{n}−\mathrm{1}\right)\pi=\left(−\mathrm{1}\right)^{\mathrm{2}{n}−\mathrm{1}} =\left(−\mathrm{1}\right)^{\mathrm{2}{n}} ×\left(−\mathrm{1}\right)=−\mathrm{1} \\ $$$$\therefore{For}\:{a}>\mathrm{0},\:{ln}\left(−{a}\right)={ln}\left({ae}^{\left(\mathrm{2}{n}−\mathrm{1}\right)\pi{i}} \right) \\ $$$${ln}\left(−{a}\right)={lna}+\left(\mathrm{2}{n}−\mathrm{1}\right)\pi{i}\:\:\:{n}\in\mathbb{Z} \\ $$$$ \\ $$$${logxy}={log}\left(−\mathrm{2}\right)=\frac{\mathrm{1}}{{ln}\mathrm{10}}\left({ln}\mathrm{2}+\left(\mathrm{2}{n}−\mathrm{1}\right)\pi{i}\right)\:\:{n}\in\mathbb{Z} \\ $$$${log}\left(−\mathrm{1}\right)=\frac{\mathrm{1}}{{ln}\mathrm{10}}\left({ln}\mathrm{1}+\left(\mathrm{2}{j}−\mathrm{1}\right)\pi{i}\right)\:\:{j}\in\mathbb{Z} \\ $$$${logx}={log}\left(−\mathrm{1}\right)=\frac{\left(\mathrm{2}{j}−\mathrm{1}\right)\pi{i}}{{ln}\mathrm{10}} \\ $$$${logy}=\frac{{ln}\mathrm{2}}{{ln}\mathrm{10}} \\ $$$$\therefore{logx}+{logy}=\frac{\mathrm{1}}{{ln}\mathrm{10}}\left({ln}\mathrm{2}+\left(\mathrm{2}{j}−\mathrm{1}\right)\pi{i}\right) \\ $$$${Let}\:{j}=\mathrm{2}\Rightarrow{logx}+{logy}=\frac{\mathrm{1}}{{ln}\mathrm{10}}\left({ln}\mathrm{2}+\mathrm{3}\pi{i}\right) \\ $$$${Let}\:{n}=\mathrm{1}\Rightarrow{logxy}=\frac{\mathrm{1}}{{ln}\mathrm{10}}\left({ln}\mathrm{2}+\pi{i}\right) \\ $$$$\therefore{logxy}={logx}+{logy} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{ln}\mathrm{10}}\left({ln}\mathrm{2}+\pi{i}\right)=\frac{\mathrm{1}}{{ln}\mathrm{10}}\left({ln}\mathrm{2}+\mathrm{3}\pi{i}\right) \\ $$$$\Rightarrow\mathrm{1}=\mathrm{3}\:{which}\:{is}\:{impossible}. \\ $$$$ \\ $$

Commented by Rasheed Soomro last updated on 20/May/16

TH𝛂NKS!

$$\mathcal{TH}\boldsymbol{\alpha}\mathcal{NKS}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com