Question and Answers Forum

All Questions      Topic List

UNKNOWN Questions

Previous in All Question      Next in All Question      

Previous in UNKNOWN      Next in UNKNOWN      

Question Number 55784 by gunawan last updated on 04/Mar/19

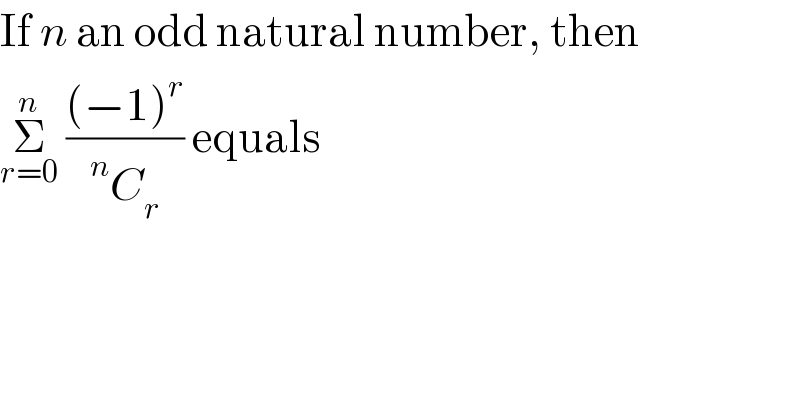
If n an odd natural number, then Σ_(r=0) ^n (((−1)^r )/(^n C_r )) equals

$$\mathrm{If}\:{n}\:\mathrm{an}\:\mathrm{odd}\:\mathrm{natural}\:\mathrm{number},\:\mathrm{then} \\ $$$$\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}\:\frac{\left(−\mathrm{1}\right)^{{r}} }{\:^{{n}} {C}_{{r}} \:}\:\mathrm{equals} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 04/Mar/19

S=T_0 +T_1 +T_2 +...+T_n =(((−1)^0 )/((n!)/(0!(n−0)!)))+(((−1)^1 )/((n!)/(1!(n−1)!)))+(((−1)^2 )/((n!)/(2!(n−2)!)))+(((−1)^3 )/((n!)/(3!(n−3)!)))+...+(((−1)^n )/((n!)/(n!(n−n)!))) =((0!(n−0)!)/(n!))−((1!(n−1)!)/(n!))+((2!(n−2)!)/(n!))−((3!(n−3)!)/(n!))+..−((n!(n−n)!)/(n!)) now look T_0 =((0!(n−0)!)/(n!))=1 T_n =((−n!(n−n)!)/(n!))=−1 T_0 +T_n =0 T_1 =((−1!(n−1)!)/(n!))=((−1)/(n−1)) T_(n−1) =(((−1)^(n−1) ×(n−1)!(1)!)/(n!))=(1/(n−1)) T_1 +T_(n−1) =0 now let n=2k+1 terms →k=((n−1)/2) middle term is (k+1)_(th) term k+1→(((n−1)/2)+1)→((n+1)/2) k+1 th term→((n+1)/2) term→(((−1)^((n+1)/2) )/(nc_((n+1)/2) )) =(((((n+1)/2))!(n−((n+1)/2))!)/(n!))→(((((n+1)/2))!(((n−1)/2))!)/(n!)) now on addition all terms ancelled each other as explained above...only one term remain so S=(((((n+1)/2))!(((n−1)/2))!)/n)←this is the answer

$${S}={T}_{\mathrm{0}} +{T}_{\mathrm{1}} +{T}_{\mathrm{2}} +...+{T}_{{n}} \\ $$$$=\frac{\left(−\mathrm{1}\right)^{\mathrm{0}} }{\frac{{n}!}{\mathrm{0}!\left({n}−\mathrm{0}\right)!}}+\frac{\left(−\mathrm{1}\right)^{\mathrm{1}} }{\frac{{n}!}{\mathrm{1}!\left({n}−\mathrm{1}\right)!}}+\frac{\left(−\mathrm{1}\right)^{\mathrm{2}} }{\frac{{n}!}{\mathrm{2}!\left({n}−\mathrm{2}\right)!}}+\frac{\left(−\mathrm{1}\right)^{\mathrm{3}} }{\frac{{n}!}{\mathrm{3}!\left({n}−\mathrm{3}\right)!}}+...+\frac{\left(−\mathrm{1}\right)^{{n}} }{\frac{{n}!}{{n}!\left({n}−{n}\right)!}} \\ $$$$ \\ $$$$=\frac{\mathrm{0}!\left({n}−\mathrm{0}\right)!}{{n}!}−\frac{\mathrm{1}!\left({n}−\mathrm{1}\right)!}{{n}!}+\frac{\mathrm{2}!\left({n}−\mathrm{2}\right)!}{{n}!}−\frac{\mathrm{3}!\left({n}−\mathrm{3}\right)!}{{n}!}+..−\frac{{n}!\left({n}−{n}\right)!}{{n}!} \\ $$$$ \\ $$$${now}\:{look}\:{T}_{\mathrm{0}} =\frac{\mathrm{0}!\left({n}−\mathrm{0}\right)!}{{n}!}=\mathrm{1} \\ $$$${T}_{{n}} =\frac{−{n}!\left({n}−{n}\right)!}{{n}!}=−\mathrm{1} \\ $$$${T}_{\mathrm{0}} +{T}_{{n}} =\mathrm{0} \\ $$$$ \\ $$$${T}_{\mathrm{1}} =\frac{−\mathrm{1}!\left({n}−\mathrm{1}\right)!}{{n}!}=\frac{−\mathrm{1}}{{n}−\mathrm{1}} \\ $$$${T}_{{n}−\mathrm{1}} =\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} ×\left({n}−\mathrm{1}\right)!\left(\mathrm{1}\right)!}{{n}!}=\frac{\mathrm{1}}{{n}−\mathrm{1}} \\ $$$${T}_{\mathrm{1}} +{T}_{{n}−\mathrm{1}} =\mathrm{0} \\ $$$$ \\ $$$${now} \\ $$$${let}\:{n}=\mathrm{2}{k}+\mathrm{1}\:{terms}\:\rightarrow{k}=\frac{{n}−\mathrm{1}}{\mathrm{2}} \\ $$$${middle}\:{term}\:{is}\:\left({k}+\mathrm{1}\right)_{{th}} \:{term} \\ $$$${k}+\mathrm{1}\rightarrow\left(\frac{{n}−\mathrm{1}}{\mathrm{2}}+\mathrm{1}\right)\rightarrow\frac{{n}+\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$${k}+\mathrm{1}\:{th}\:{term}\rightarrow\frac{{n}+\mathrm{1}}{\mathrm{2}}\:{term}\rightarrow\frac{\left(−\mathrm{1}\right)^{\frac{{n}+\mathrm{1}}{\mathrm{2}}} }{{nc}_{\frac{{n}+\mathrm{1}}{\mathrm{2}}} } \\ $$$$=\frac{\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}\right)!\left({n}−\frac{{n}+\mathrm{1}}{\mathrm{2}}\right)!}{{n}!}\rightarrow\frac{\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}\right)!\left(\frac{{n}−\mathrm{1}}{\mathrm{2}}\right)!}{{n}!} \\ $$$$ \\ $$$${now}\:{on}\:{addition}\:{all}\:{terms}\:{ancelled}\:{each}\:{other} \\ $$$${as}\:{explained}\:{above}...{only}\:{one}\:{term}\:{remain} \\ $$$${so}\:\boldsymbol{{S}}=\frac{\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}\right)!\left(\frac{{n}−\mathrm{1}}{\mathrm{2}}\right)!}{{n}}\leftarrow{this}\:{is}\:{the}\:{answer} \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com