For what values of p the integral ∫_0 ^1 x^p ln x dx converge?


Question and Answers Forum

All Questions Topic List
Others Questions
Previous in All Question Next in All Question
Previous in Others Next in Others
Question Number 55856 by Joel578 last updated on 05/Mar/19

$For what values of p the integral$ $\int_{0}^{1} x^{p} \ln x d x$ $converge ?$
Commented by maxmathsup by imad last updated on 05/Mar/19

$l e t A_{p} = \int_{0}^{1} x^{p} l n (x) d x c h a n g e m e n t l n (x) = - t g i v e x = e^{- t}$ $A_{p} = - \int_{0}^{\infty} {(e^{- t})}^{p} (t) e^{- t} d t = - \int_{0}^{\infty} t e^{- (p + 1) t} d t$ $i f p > - 1 A_{p} c o n v e r g e s i f p ⩽ - 1 {l i m}_{t \to + \infty} t e^{- (p + 1) t} = + \infty \Rightarrow A_{p} d i v e r g e s$
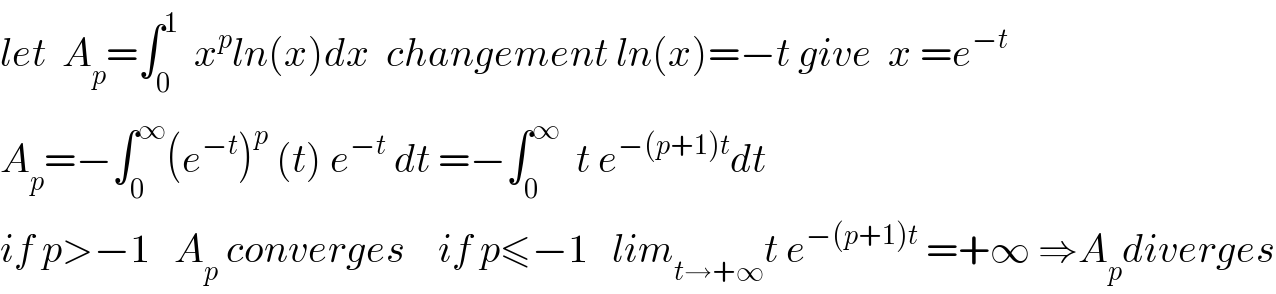
	Answered by tanmay.chaudhury50@gmail.com last updated on 05/Mar/19
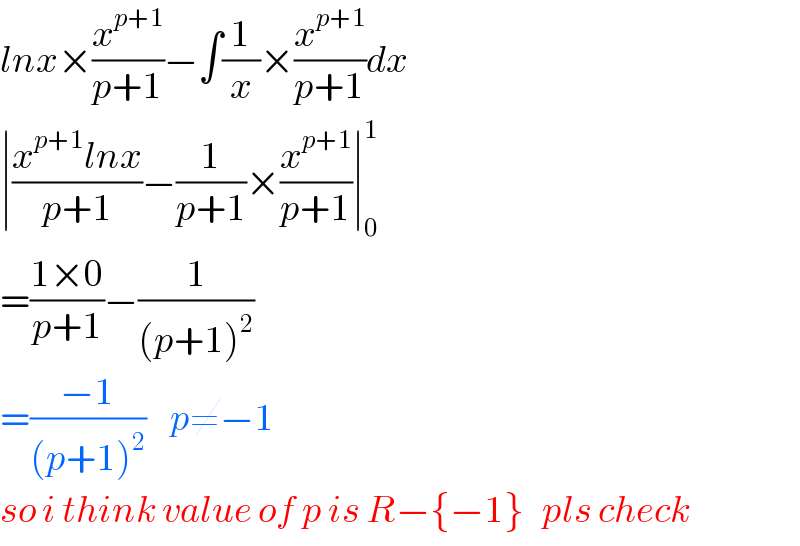
	$lnx×(x^(p+1) /(p+1))−∫(1/x)×(x^(p+1) /(p+1))dx ∣((x^(p+1) lnx)/(p+1))−(1/(p+1))×(x^(p+1) /(p+1))∣_0 ^1 =((1×0)/(p+1))−(1/((p+1)^2 )) =((−1)/((p+1)^2 )) p≠−1 so i think value of p is R−{−1} pls check$
	$l n x \times \frac{x^{p + 1}}{p + 1} - \int \frac{1}{x} \times \frac{x^{p + 1}}{p + 1} d x$ $∣ \frac{x^{p + 1} l n x}{p + 1} - \frac{1}{p + 1} \times \frac{x^{p + 1}}{p + 1} ∣_{0}^{1}$ $= \frac{1 \times 0}{p + 1} - \frac{1}{{(p + 1)}^{2}}$ $= \frac{- 1}{{(p + 1)}^{2}} p \neq - 1$ $s o i t h i n k v a l u e o f p i s R - {- 1} p l s c h e c k$
	Commented by tanmay.chaudhury50@gmail.com last updated on 05/Mar/19

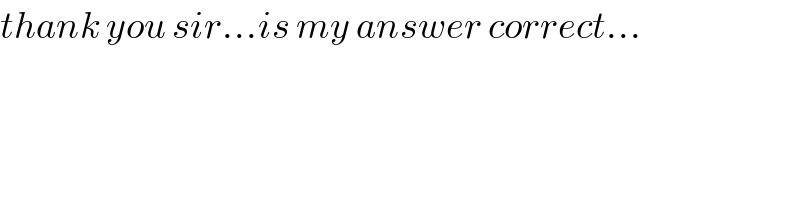
	$t h a n k y o u s i r . . . i s m y a n s w e r c o r r e c t . . .$
	Commented by Joel578 last updated on 05/Mar/19
	$Sir I think p should be ≤ −1 I =lim_(t→0^+ ) [((x^(p+1) (ln x))/(p + 1)) − (x^(p+1) /((p + 1)^2 ))]_t ^1 ⇒ lim_(t→0^+ ) {(0 − (1/((p + 1)^2 ))) − (((t^(p+1) (ln t))/(p + 1)) − (t^(p+1) /((p + 1)^2 )))} ⇒ − (1/((p + 1)^2 )) − lim_(t→0^+ ) {(t^(p+1) /(p + 1))(ln t − (1/(p + 1)))} when p + 1 = 0 ⇔ p = −1, I diverge when p + 1 < 0 ⇔ p < − 1, (p + 1) is negative, which mean t^(p+1) → ∞ as t → 0^+ . Hence I = −(1/((p + 1)^2 )) − ∞ = −∞ (diverge)$
	$Sir I think p should be ⩽ - 1$ $I = \lim_{t \to 0^{+}} {[\frac{x^{p + 1} (\ln x)}{p + 1} - \frac{x^{p + 1}}{{(p + 1)}^{2}}]}_{t}^{1}$ $\Rightarrow \lim_{t \to 0^{+}} {(0 - \frac{1}{{(p + 1)}^{2}}) - (\frac{t^{p + 1} (\ln t)}{p + 1} - \frac{t^{p + 1}}{{(p + 1)}^{2}})}$ $\Rightarrow - \frac{1}{{(p + 1)}^{2}} - \lim_{t \to 0^{+}} {\frac{t^{p + 1}}{p + 1} (\ln t - \frac{1}{p + 1})}$ $when p + 1 = 0 \Leftrightarrow p = - 1, I diverge$ $when p + 1 < 0 \Leftrightarrow p < - 1, (p + 1) is negative,$ $which mean t^{p + 1} \to \infty as t \to 0^{+} .$ $Hence I = - \frac{1}{{(p + 1)}^{2}} - \infty = - \infty (diverge)$
	Commented by Joel578 last updated on 05/Mar/19

	$please correct if I am wrong$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum