
Question and Answers Forum
Question Number 55887 by behi83417@gmail.com last updated on 05/Mar/19

Answered by MJS last updated on 05/Mar/19

Answered by JDamian last updated on 06/Mar/19
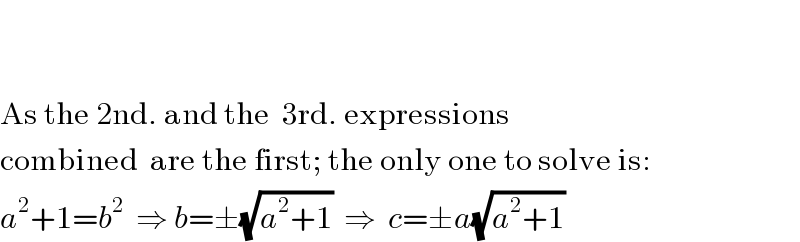
| ||
Question and Answers Forum | ||
Question Number 55887 by behi83417@gmail.com last updated on 05/Mar/19 | ||
 | ||
Answered by MJS last updated on 05/Mar/19 | ||
 | ||
| ||
Answered by JDamian last updated on 06/Mar/19 | ||
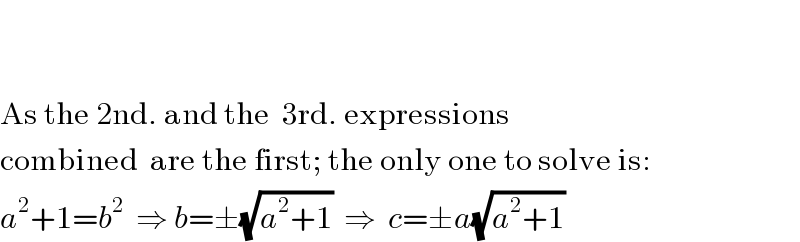 | ||
| ||