
Question and Answers Forum
Question Number 55907 by gunawan last updated on 06/Mar/19
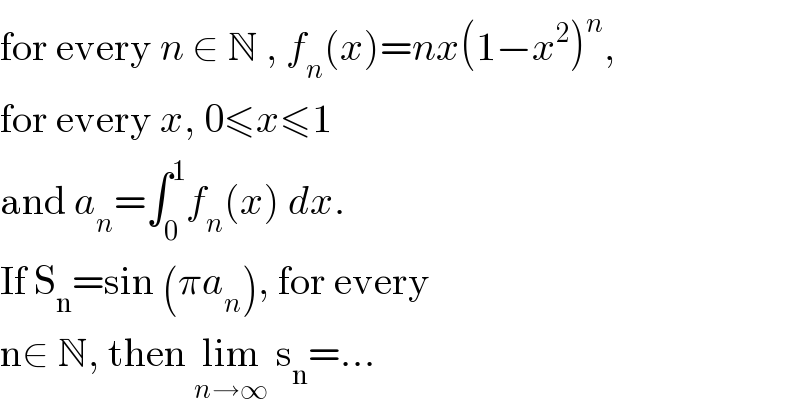
Commented by maxmathsup by imad last updated on 06/Mar/19
![we have a_n =∫_0 ^1 nx(1−x^2 )^n dx ⇒πa_n =nπ ∫_0 ^1 x(1−x^2 )^n dx but ∫_0 ^1 x(1−x^2 )^n dx =−(1/(2(n+1)))[(1−x^2 )^(n+1) ]_0 ^1 =(1/(2n+2)) ⇒πa_n =((nπ)/(2n+2)) =((nπ)/(2n(1+(1/n)))) =(π/(2(1+(1/n)))) ∼(π/2)(1−(1/n)) (n→+∞ ⇒sin(πa_n )∼sin((π/2)−(π/(2n))) ⇒lim_(n→+∞) S_n =sin((π/2)) =1 .](Q55953.png)
Answered by 121194 last updated on 06/Mar/19
![a_n =∫_0 ^1 nx(1−x^2 )^n dx y=1−x^2 ⇒dy=−2xdx⇒xdx=−(dy/2) x=0⇒y=1 x=1⇒y=0 a_n =n∫_0 ^1 (1−x^2 )^n xdx=−(n/2)∫_1 ^0 y^n dy=(n/2)∫_0 ^1 y^n dy =(n/(2(n+1))) lim_(n→∞) sin [((πn)/(2(n+1)))]=sin ((π/2)lim_(n→∞) (n/(n+1)))=sin (π/2)=1](Q55935.png)
| ||
Question and Answers Forum | ||
Question Number 55907 by gunawan last updated on 06/Mar/19 | ||
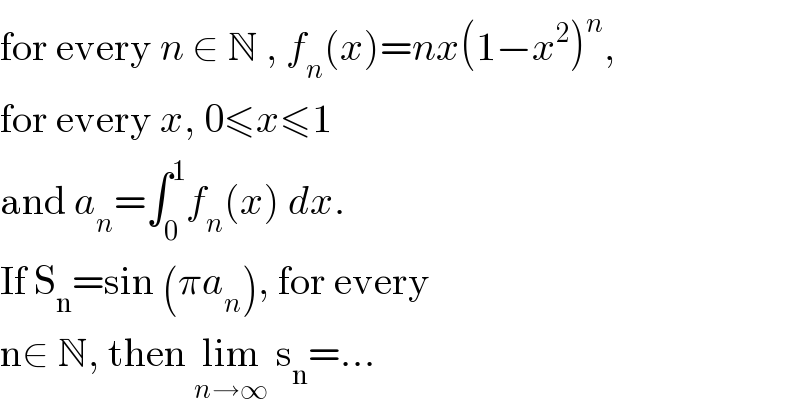 | ||
Commented by maxmathsup by imad last updated on 06/Mar/19 | ||
![we have a_n =∫_0 ^1 nx(1−x^2 )^n dx ⇒πa_n =nπ ∫_0 ^1 x(1−x^2 )^n dx but ∫_0 ^1 x(1−x^2 )^n dx =−(1/(2(n+1)))[(1−x^2 )^(n+1) ]_0 ^1 =(1/(2n+2)) ⇒πa_n =((nπ)/(2n+2)) =((nπ)/(2n(1+(1/n)))) =(π/(2(1+(1/n)))) ∼(π/2)(1−(1/n)) (n→+∞ ⇒sin(πa_n )∼sin((π/2)−(π/(2n))) ⇒lim_(n→+∞) S_n =sin((π/2)) =1 .](Q55953.png) | ||
Answered by 121194 last updated on 06/Mar/19 | ||
![a_n =∫_0 ^1 nx(1−x^2 )^n dx y=1−x^2 ⇒dy=−2xdx⇒xdx=−(dy/2) x=0⇒y=1 x=1⇒y=0 a_n =n∫_0 ^1 (1−x^2 )^n xdx=−(n/2)∫_1 ^0 y^n dy=(n/2)∫_0 ^1 y^n dy =(n/(2(n+1))) lim_(n→∞) sin [((πn)/(2(n+1)))]=sin ((π/2)lim_(n→∞) (n/(n+1)))=sin (π/2)=1](Q55935.png) | ||
| ||