
Question and Answers Forum
Question Number 55991 by bshahid010@gmail.com last updated on 07/Mar/19
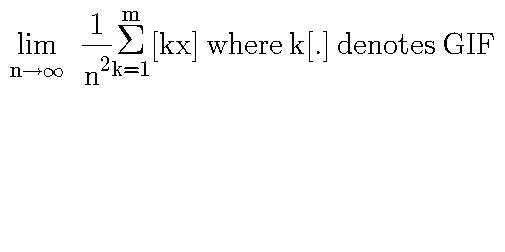
Commented by maxmathsup by imad last updated on 07/Mar/19
![let S_n (x)=(1/n^2 ) Σ_(k=1) ^m [kx]we have [kx]≤kx<[kx]+1 ⇒ kx−1<[kx]≤kx ⇒ (1/n^2 )Σ_(k=1) ^m (kx−1)<(1/n^2 )Σ_(k=1) ^m [kx)≤(1/n^2 )Σ_(k=1) ^m kx but (1/n^2 )Σ_(k=1) ^m (kx−1) =x ((Σ_(k=1) ^m k)/n^2 ) −(m/n^2 ) =x ((m(m+1))/(2n^2 )) −(m/n^2 ) =A_n also (1/n^2 )Σ_(k=1) ^m kx =x ((m(m+1))/n) =B_m if m is fixed lim_(n→+∞) A_n =0 and lim_(n→+∞) B_n =0 ⇒lim S_n (x)=0 if m is function of n its aother subject let suppose m ∼n ⇒ lim_(n→+∞) A_n =(x/2) =lim_(n→+∞) B_n ⇒lim_(n→+∞) S_n (x)=(x/2) .](Q56003.png)
Commented by maxmathsup by imad last updated on 07/Mar/19
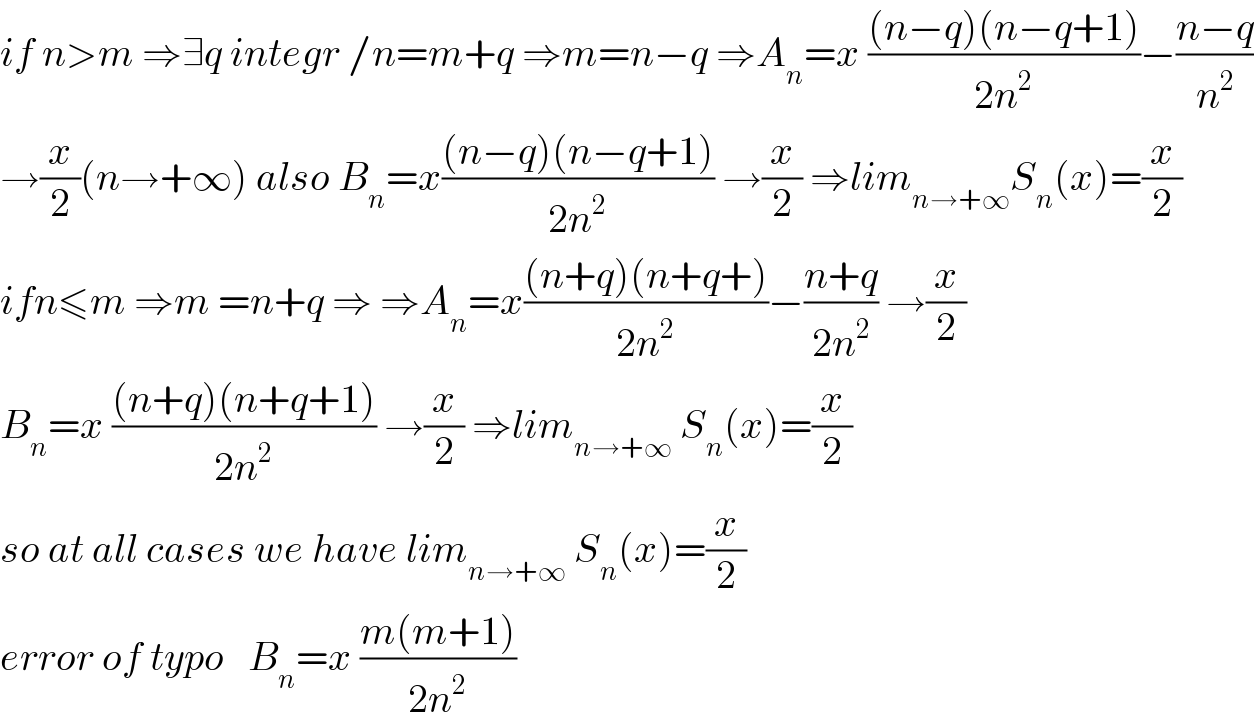
| ||
Question and Answers Forum | ||
Question Number 55991 by bshahid010@gmail.com last updated on 07/Mar/19 | ||
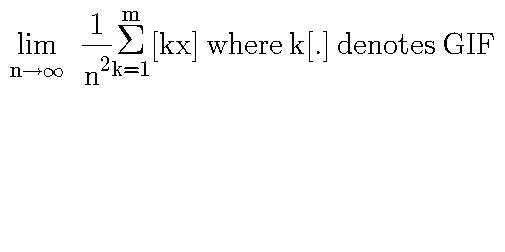 | ||
Commented by maxmathsup by imad last updated on 07/Mar/19 | ||
![let S_n (x)=(1/n^2 ) Σ_(k=1) ^m [kx]we have [kx]≤kx<[kx]+1 ⇒ kx−1<[kx]≤kx ⇒ (1/n^2 )Σ_(k=1) ^m (kx−1)<(1/n^2 )Σ_(k=1) ^m [kx)≤(1/n^2 )Σ_(k=1) ^m kx but (1/n^2 )Σ_(k=1) ^m (kx−1) =x ((Σ_(k=1) ^m k)/n^2 ) −(m/n^2 ) =x ((m(m+1))/(2n^2 )) −(m/n^2 ) =A_n also (1/n^2 )Σ_(k=1) ^m kx =x ((m(m+1))/n) =B_m if m is fixed lim_(n→+∞) A_n =0 and lim_(n→+∞) B_n =0 ⇒lim S_n (x)=0 if m is function of n its aother subject let suppose m ∼n ⇒ lim_(n→+∞) A_n =(x/2) =lim_(n→+∞) B_n ⇒lim_(n→+∞) S_n (x)=(x/2) .](Q56003.png) | ||
Commented by maxmathsup by imad last updated on 07/Mar/19 | ||
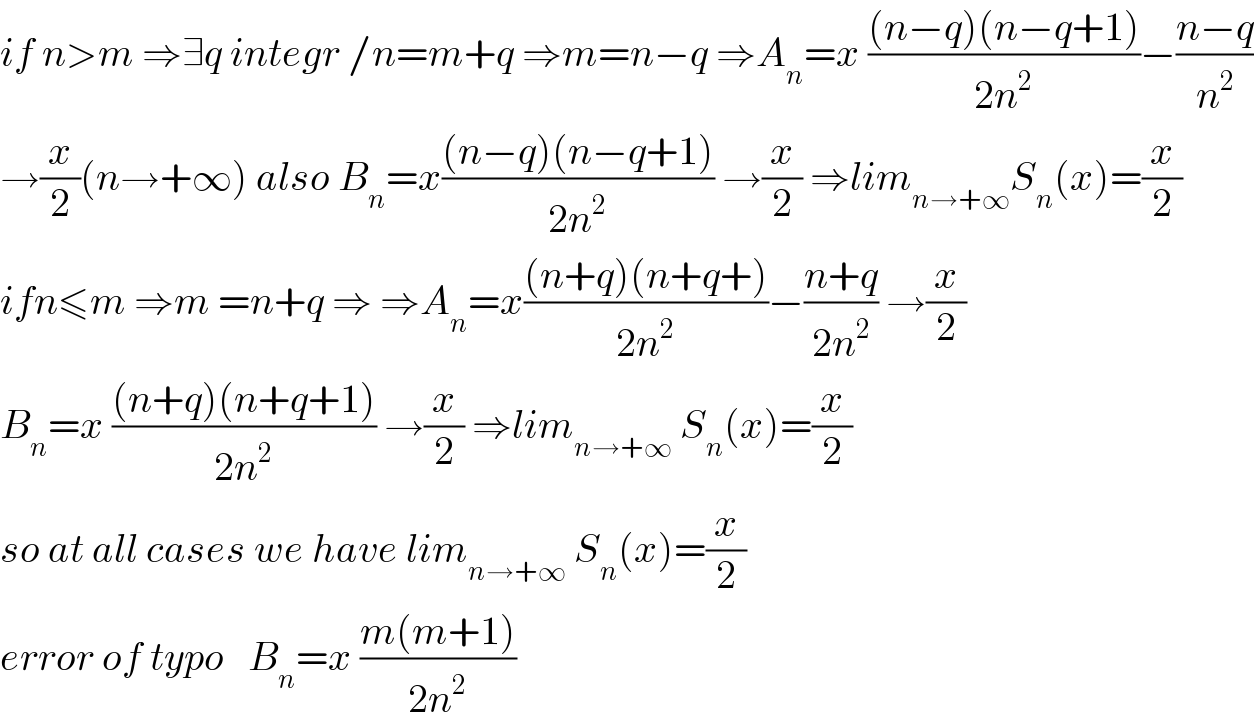 | ||