
Question and Answers Forum
Question Number 55992 by Mikael_Marshall last updated on 07/Mar/19

Commented by mr W last updated on 07/Mar/19
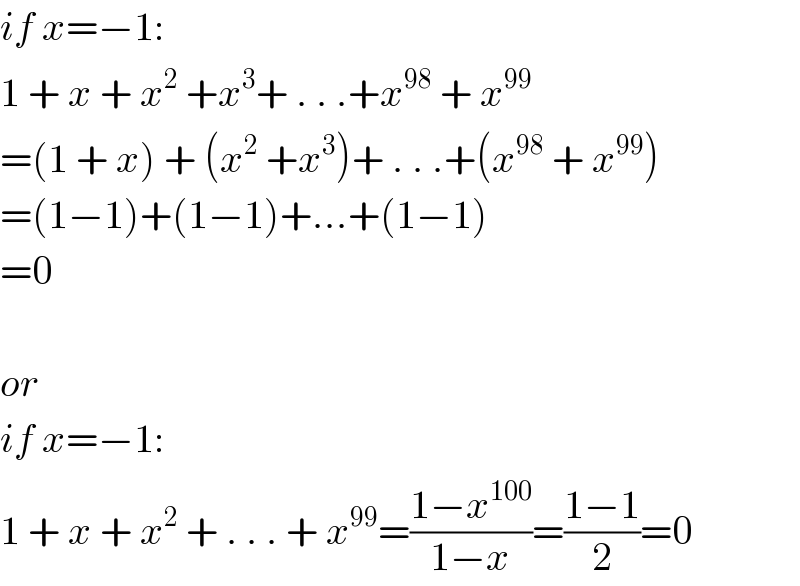
Commented by maxmathsup by imad last updated on 07/Mar/19
![if x from C (e) ⇔ ((1−x^(100) )/(1−x)) =0 with x≠1 ⇒x^(100) =1 =e^(i2kπ) ⇒ x_k =e^((ikπ)/(50)) and k∈[[1,99]] are roots of this equation.](Q56002.png)
| ||
Question and Answers Forum | ||
Question Number 55992 by Mikael_Marshall last updated on 07/Mar/19 | ||
 | ||
Commented by mr W last updated on 07/Mar/19 | ||
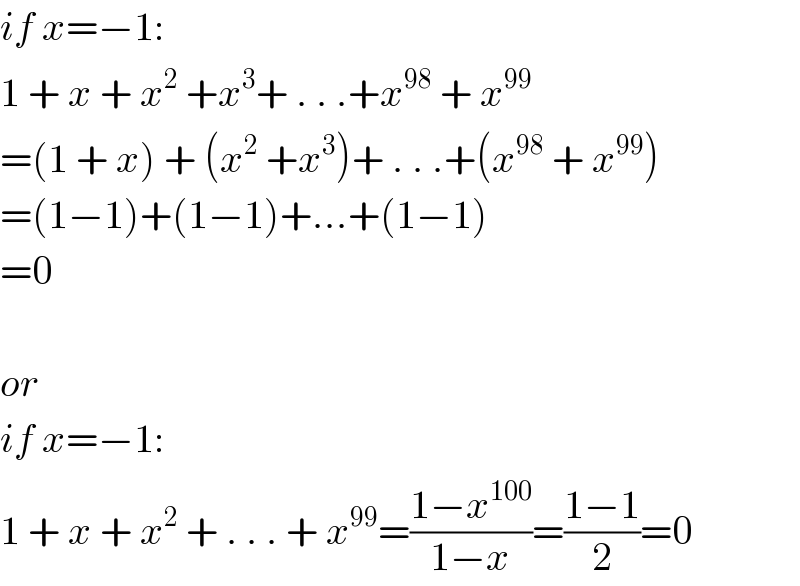 | ||
Commented by maxmathsup by imad last updated on 07/Mar/19 | ||
![if x from C (e) ⇔ ((1−x^(100) )/(1−x)) =0 with x≠1 ⇒x^(100) =1 =e^(i2kπ) ⇒ x_k =e^((ikπ)/(50)) and k∈[[1,99]] are roots of this equation.](Q56002.png) | ||