Question Number 56037 by ajfour last updated on 08/Mar/19
Commented by ajfour last updated on 08/Mar/19
$${Find}\:{maximum}\:{area}\:{of}\:{inner} \\ $$$${triangle}\:{if}\:{outer}\:{one}\:{is}\:{equilateral}. \\ $$
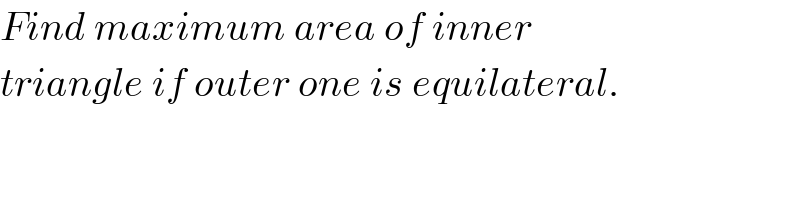
Commented by mr W last updated on 08/Mar/19
$${is}\:{it}\:{not}\:{when}\:{inner}\:{triangle}\:{is}\:{equal} \\ $$$${to}\:{the}\:{outer}\:{one}? \\ $$
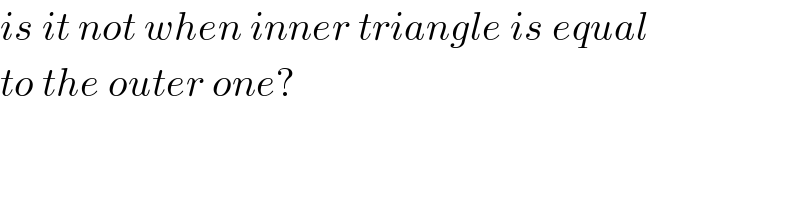
Commented by 121194 last updated on 08/Mar/19
$$\mathrm{are}\:\mathrm{you}\:\mathrm{sure}\:\mathrm{there}\:\mathrm{not}\:\mathrm{any}\:\mathrm{additional}\:\mathrm{condition}\:\mathrm{there}? \\ $$
Commented by ajfour last updated on 08/Mar/19
$${a},\:{b},\:{c}\:{are}\:{not}\:{equal}. \\ $$
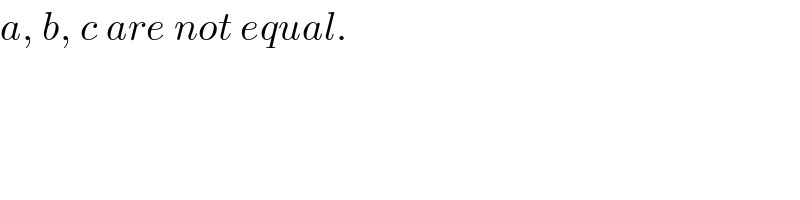
Commented by mr W last updated on 09/Mar/19
$${thank}\:{you}\:{for}\:{clarifing}\:{sir}! \\ $$$${a},{b},{c}\:{are}\:{given}\:{and}\:{there}\:{are}\:{many} \\ $$$${cases},\:{so}\:{the}\:{question}\:{is}\:{hard}. \\ $$
Answered by ajfour last updated on 11/Mar/19
![let side of equilateral △ be s. ⇒ 3s=a+b+c let bottom segments be x and s−x. The right side segments are c−s+x and 2s−x−c. The left side segments are s−b+x, and b−x. For the inner △ area to be maximum, The remaining area has to be minimum. The blue area A=(1/2)sin 60°[x(b−x)+(s−x)(c−s+x) +(2s−c−x)(s−b+x) (dA/dx)=((√3)/4)[(b−x−x)+(−c+s−x+s −x)+(−s+b−x+2s−c−x) ]= 0 ⇒ 3s−6x+2b−2c = 0 (a+b+c)+2b−2c = 6x ⇒ x_0 =((a+3b−c)/6) (d^2 A/dx^2 )= −6 ⇒ A is maximum for x_0 =((a+3b−c)/6) . ⇒ b−x = ((−a+3b+c)/6) Minimum inner △ area A is =((√3)/(36))(a+b+c)^2 −((3(√3))/4)(((9b^2 −(c−a)^2 )/(36))) =((√3)/(36))(a+b+c)^2 − (((√3)[9b^2 −(c−a)^2 ])/(48)) .](Q56122.png)
$${let}\:{side}\:{of}\:{equilateral}\:\bigtriangleup\:{be}\:{s}. \\ $$$$\Rightarrow\:\:\mathrm{3}{s}={a}+{b}+{c} \\ $$$${let}\:{bottom}\:{segments}\:{be}\:\boldsymbol{{x}}\:{and}\:\boldsymbol{{s}}−\boldsymbol{{x}}. \\ $$$${The}\:{right}\:{side}\:{segments}\:{are}\: \\ $$$$\boldsymbol{{c}}−\boldsymbol{{s}}+\boldsymbol{{x}}\:{and}\:\mathrm{2}\boldsymbol{{s}}−\boldsymbol{{x}}−\boldsymbol{{c}}. \\ $$$${The}\:{left}\:{side}\:{segments}\:{are} \\ $$$$\:\:\boldsymbol{{s}}−\boldsymbol{{b}}+\boldsymbol{{x}},\:{and}\:\:\boldsymbol{{b}}−\boldsymbol{{x}}. \\ $$$${For}\:{the}\:{inner}\:\bigtriangleup\:{area}\:{to}\:{be}\:{maximum}, \\ $$$${The}\:{remaining}\:{area}\:{has}\:{to}\:{be} \\ $$$${minimum}. \\ $$$${The}\:{blue}\:{area}\: \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{60}°\left[{x}\left({b}−{x}\right)+\left({s}−{x}\right)\left({c}−{s}+{x}\right)\right. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\left(\mathrm{2}{s}−{c}−{x}\right)\left({s}−{b}+{x}\right) \\ $$$$\frac{{dA}}{{dx}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\left[\left({b}−{x}−{x}\right)+\left(−{c}+{s}−{x}+{s}\right.\right. \\ $$$$\left.\:\left.\:\:\:\:\:\:\:−{x}\right)+\left(−{s}+{b}−{x}+\mathrm{2}{s}−{c}−{x}\right)\:\right]=\:\mathrm{0} \\ $$$$\Rightarrow\:\:\mathrm{3}{s}−\mathrm{6}{x}+\mathrm{2}{b}−\mathrm{2}{c}\:=\:\mathrm{0} \\ $$$$\:\:\:\:\:\left({a}+{b}+{c}\right)+\mathrm{2}{b}−\mathrm{2}{c}\:=\:\mathrm{6}{x} \\ $$$$\Rightarrow\:\:\:{x}_{\mathrm{0}} =\frac{{a}+\mathrm{3}{b}−{c}}{\mathrm{6}} \\ $$$$\:\:\frac{{d}^{\mathrm{2}} {A}}{{dx}^{\mathrm{2}} }=\:−\mathrm{6}\:\:\Rightarrow\:{A}\:{is}\:{maximum}\:{for} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}_{\mathrm{0}} =\frac{{a}+\mathrm{3}{b}−{c}}{\mathrm{6}}\:. \\ $$$$\Rightarrow\:\:\:{b}−{x}\:=\:\frac{−{a}+\mathrm{3}{b}+{c}}{\mathrm{6}} \\ $$$${Minimum}\:{inner}\:\bigtriangleup\:{area}\:{A}\:{is} \\ $$$$\:\:\:\:\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{36}}\left({a}+{b}+{c}\right)^{\mathrm{2}} −\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{4}}\left(\frac{\mathrm{9}{b}^{\mathrm{2}} −\left({c}−{a}\right)^{\mathrm{2}} }{\mathrm{36}}\right) \\ $$$$\:\:\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{36}}\left({a}+{b}+{c}\right)^{\mathrm{2}} −\:\frac{\sqrt{\mathrm{3}}\left[\mathrm{9}{b}^{\mathrm{2}} −\left({c}−{a}\right)^{\mathrm{2}} \right]}{\mathrm{48}}\:. \\ $$
Commented by mr W last updated on 10/Mar/19
$${very}\:{nice}\:{sir}!\:{is}\:{this}\:{the}\:{mininum} \\ $$$${inner}\:{triangle}\:{or}\:{the}\:{maximum}? \\ $$
Commented by ajfour last updated on 11/Mar/19
$${unfortunately}\:{its}\:{the}\:{minimum} \\ $$$${area}\:{Sir}! \\ $$