Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 56074 by Kunal12588 last updated on 10/Mar/19

In a sequence if r^(th) term is given by T_r =2×T_(r−1) +1 then give it′s n^(th) term in terms of it′s 1^(st) term [Given : T_1 =2]

$${In}\:{a}\:{sequence}\:{if}\:{r}^{{th}} \:{term}\:{is}\:{given}\:{by} \\ $$$${T}_{{r}} =\mathrm{2}×{T}_{{r}−\mathrm{1}} +\mathrm{1} \\ $$$${then}\:{give}\:{it}'{s}\:{n}^{{th}} \:{term}\:{in}\:{terms}\:{of}\:\:{it}'{s}\:\mathrm{1}^{{st}} \:{term} \\ $$$$\left[{Given}\::\:\:\:\:\:{T}_{\mathrm{1}} =\mathrm{2}\right] \\ $$

Commented by maxmathsup by imad last updated on 10/Mar/19

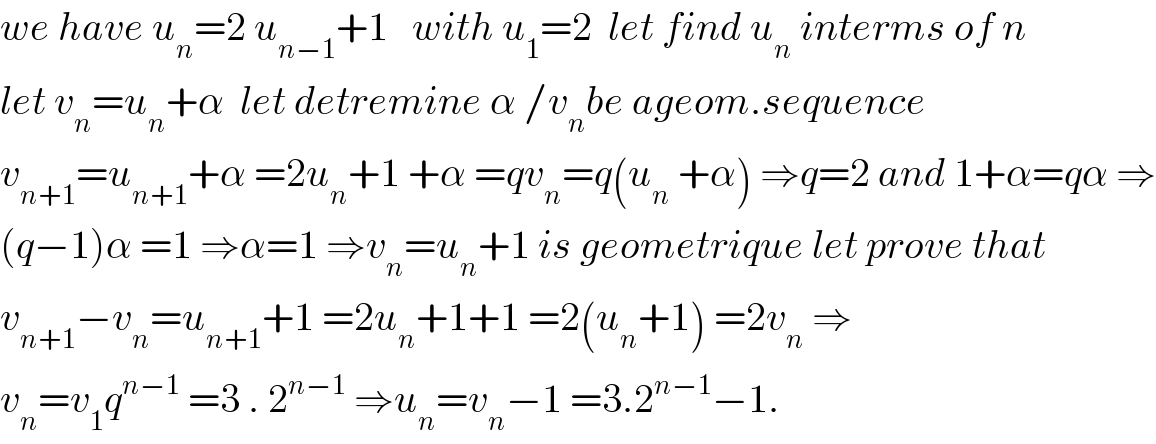
we have u_n =2 u_(n−1) +1 with u_1 =2 let find u_n interms of n let v_n =u_n +α let detremine α /v_n be ageom.sequence v_(n+1) =u_(n+1) +α =2u_n +1 +α =qv_n =q(u_n +α) ⇒q=2 and 1+α=qα ⇒ (q−1)α =1 ⇒α=1 ⇒v_n =u_n +1 is geometrique let prove that v_(n+1) −v_n =u_(n+1) +1 =2u_n +1+1 =2(u_n +1) =2v_n ⇒ v_n =v_1 q^(n−1) =3 . 2^(n−1) ⇒u_n =v_n −1 =3.2^(n−1) −1.

$${we}\:{have}\:{u}_{{n}} =\mathrm{2}\:{u}_{{n}−\mathrm{1}} +\mathrm{1}\:\:\:{with}\:{u}_{\mathrm{1}} =\mathrm{2}\:\:{let}\:{find}\:{u}_{{n}} \:{interms}\:{of}\:{n} \\ $$$${let}\:{v}_{{n}} ={u}_{{n}} +\alpha\:\:{let}\:{detremine}\:\alpha\:/{v}_{{n}} {be}\:{ageom}.{sequence} \\ $$$${v}_{{n}+\mathrm{1}} ={u}_{{n}+\mathrm{1}} +\alpha\:=\mathrm{2}{u}_{{n}} +\mathrm{1}\:+\alpha\:={qv}_{{n}} ={q}\left({u}_{{n}} \:+\alpha\right)\:\Rightarrow{q}=\mathrm{2}\:{and}\:\mathrm{1}+\alpha={q}\alpha\:\Rightarrow \\ $$$$\left({q}−\mathrm{1}\right)\alpha\:=\mathrm{1}\:\Rightarrow\alpha=\mathrm{1}\:\Rightarrow{v}_{{n}} ={u}_{{n}} +\mathrm{1}\:{is}\:{geometrique}\:{let}\:{prove}\:{that} \\ $$$${v}_{{n}+\mathrm{1}} −{v}_{{n}} ={u}_{{n}+\mathrm{1}} +\mathrm{1}\:=\mathrm{2}{u}_{{n}} +\mathrm{1}+\mathrm{1}\:=\mathrm{2}\left({u}_{{n}} +\mathrm{1}\right)\:=\mathrm{2}{v}_{{n}} \:\Rightarrow \\ $$$${v}_{{n}} ={v}_{\mathrm{1}} {q}^{{n}−\mathrm{1}} \:=\mathrm{3}\:.\:\mathrm{2}^{{n}−\mathrm{1}} \:\Rightarrow{u}_{{n}} ={v}_{{n}} −\mathrm{1}\:=\mathrm{3}.\mathrm{2}^{{n}−\mathrm{1}} −\mathrm{1}. \\ $$

Commented by maxmathsup by imad last updated on 10/Mar/19

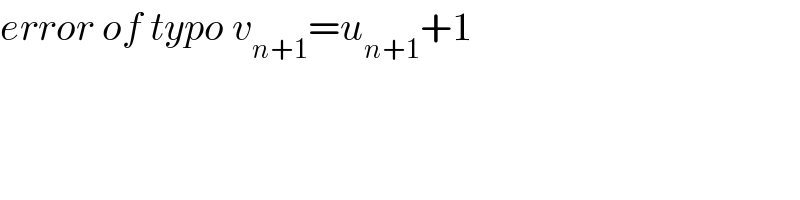
error of typo v_(n+1) =u_(n+1) +1

$${error}\:{of}\:{typo}\:{v}_{{n}+\mathrm{1}} ={u}_{{n}+\mathrm{1}} +\mathrm{1} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 10/Mar/19

T_2 =2T_1 +1→2×2+1→2^2 +2^0 T_3 =2T_2 +1→2(2^2 +1)+1→2^3 +2^1 +2^0 T_4 =2T_3 +1→2(2^3 +2^1 +2^0 )+1→2^4 +2^2 +2^1 +1 T_5 =2T_4 +1→2(2^4 +2^2 +2^1 +1)+1→2^5 +2^3 +2^2 +2^1 +1 ... T_n =2^n +2^(n−2) +2^(n−3) +2^(n−4) +...+1←total n terms T_n =2^n +((2^(n−2) (1−(1/2^(n−1) )))/((1−(1/2))))[s=((a(1−r^n ))/((1−r)))] T_n =2^n +2^(n−1) (1−(1/2^(n−1) )) T_n =2^n +2^(n−1) −1 →it is the answer

$${T}_{\mathrm{2}} =\mathrm{2}{T}_{\mathrm{1}} +\mathrm{1}\rightarrow\mathrm{2}×\mathrm{2}+\mathrm{1}\rightarrow\mathrm{2}^{\mathrm{2}} +\mathrm{2}^{\mathrm{0}} \\ $$$${T}_{\mathrm{3}} =\mathrm{2}{T}_{\mathrm{2}} +\mathrm{1}\rightarrow\mathrm{2}\left(\mathrm{2}^{\mathrm{2}} +\mathrm{1}\right)+\mathrm{1}\rightarrow\mathrm{2}^{\mathrm{3}} +\mathrm{2}^{\mathrm{1}} +\mathrm{2}^{\mathrm{0}} \\ $$$${T}_{\mathrm{4}} =\mathrm{2}{T}_{\mathrm{3}} +\mathrm{1}\rightarrow\mathrm{2}\left(\mathrm{2}^{\mathrm{3}} +\mathrm{2}^{\mathrm{1}} +\mathrm{2}^{\mathrm{0}} \right)+\mathrm{1}\rightarrow\mathrm{2}^{\mathrm{4}} +\mathrm{2}^{\mathrm{2}} +\mathrm{2}^{\mathrm{1}} +\mathrm{1} \\ $$$${T}_{\mathrm{5}} =\mathrm{2}{T}_{\mathrm{4}} +\mathrm{1}\rightarrow\mathrm{2}\left(\mathrm{2}^{\mathrm{4}} +\mathrm{2}^{\mathrm{2}} +\mathrm{2}^{\mathrm{1}} +\mathrm{1}\right)+\mathrm{1}\rightarrow\mathrm{2}^{\mathrm{5}} +\mathrm{2}^{\mathrm{3}} +\mathrm{2}^{\mathrm{2}} +\mathrm{2}^{\mathrm{1}} +\mathrm{1} \\ $$$$... \\ $$$${T}_{{n}} =\mathrm{2}^{{n}} +\mathrm{2}^{{n}−\mathrm{2}} +\mathrm{2}^{{n}−\mathrm{3}} +\mathrm{2}^{{n}−\mathrm{4}} +...+\mathrm{1}\leftarrow{total}\:{n}\:{terms} \\ $$$${T}_{{n}} =\mathrm{2}^{{n}} +\frac{\mathrm{2}^{{n}−\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }\right)}{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)}\left[{s}=\frac{{a}\left(\mathrm{1}−{r}^{{n}} \right)}{\left(\mathrm{1}−{r}\right)}\right] \\ $$$${T}_{{n}} =\mathrm{2}^{{n}} +\mathrm{2}^{{n}−\mathrm{1}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }\right) \\ $$$${T}_{{n}} =\mathrm{2}^{{n}} +\mathrm{2}^{{n}−\mathrm{1}} −\mathrm{1}\:\rightarrow{it}\:{is}\:{the}\:{answer} \\ $$

Commented by Kunal12588 last updated on 10/Mar/19

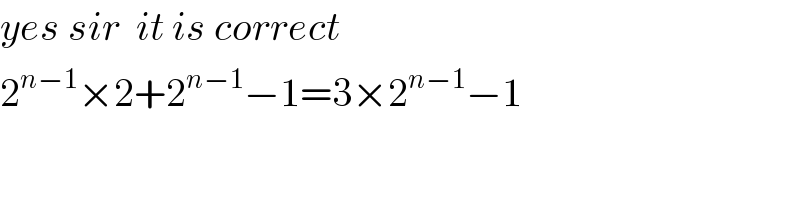
yes sir it is correct 2^(n−1) ×2+2^(n−1) −1=3×2^(n−1) −1

$${yes}\:{sir}\:\:{it}\:{is}\:{correct} \\ $$$$\mathrm{2}^{{n}−\mathrm{1}} ×\mathrm{2}+\mathrm{2}^{{n}−\mathrm{1}} −\mathrm{1}=\mathrm{3}×\mathrm{2}^{{n}−\mathrm{1}} −\mathrm{1} \\ $$

Commented by Kunal12588 last updated on 10/Mar/19

thank you

$${thank}\:{you} \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 10/Mar/19

thank you sir...

$${thank}\:{you}\:{sir}... \\ $$

Answered by mr W last updated on 10/Mar/19

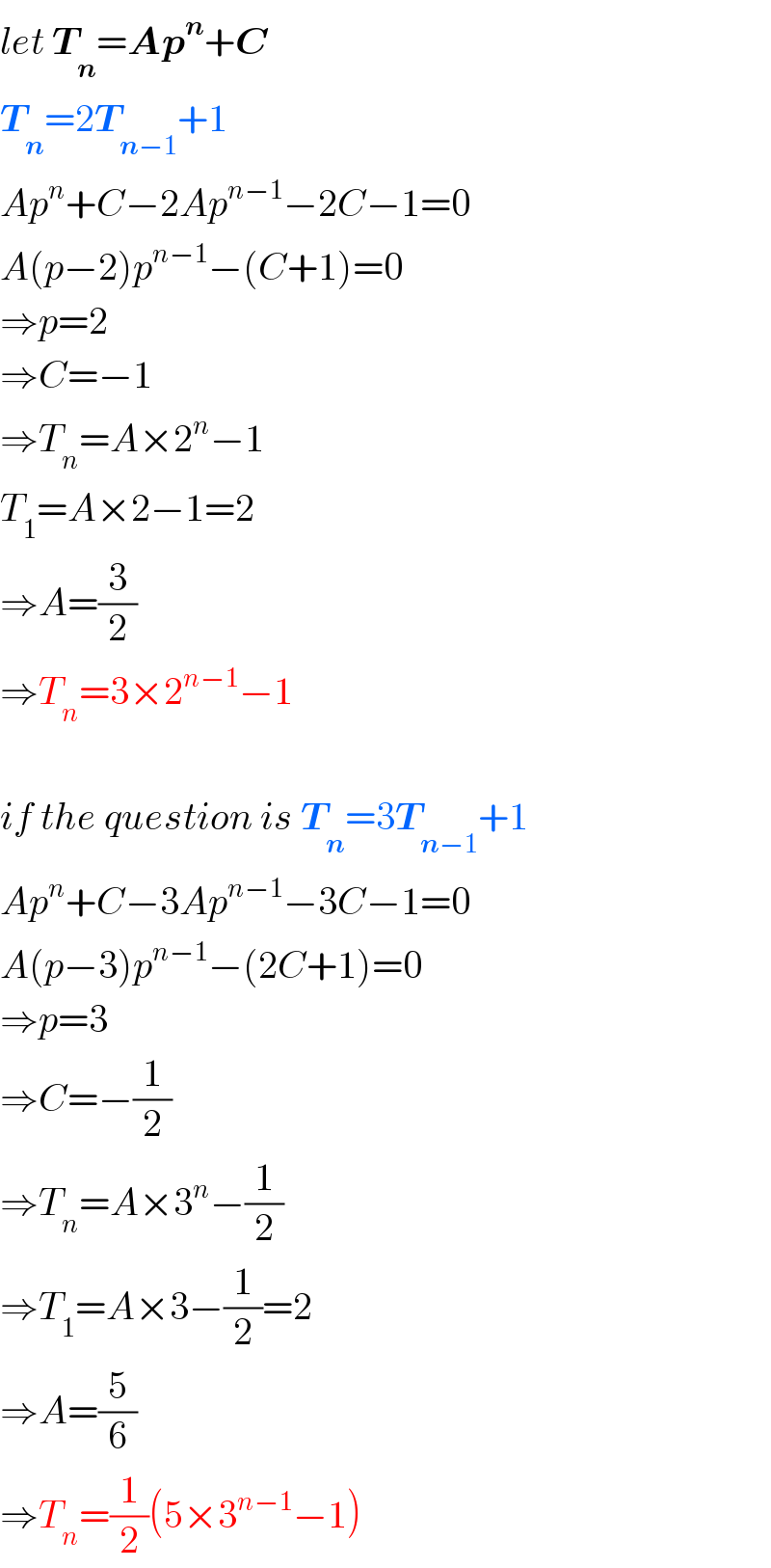
let T_n =Ap^n +C T_n =2T_(n−1) +1 Ap^n +C−2Ap^(n−1) −2C−1=0 A(p−2)p^(n−1) −(C+1)=0 ⇒p=2 ⇒C=−1 ⇒T_n =A×2^n −1 T_1 =A×2−1=2 ⇒A=(3/2) ⇒T_n =3×2^(n−1) −1 if the question is T_n =3T_(n−1) +1 Ap^n +C−3Ap^(n−1) −3C−1=0 A(p−3)p^(n−1) −(2C+1)=0 ⇒p=3 ⇒C=−(1/2) ⇒T_n =A×3^n −(1/2) ⇒T_1 =A×3−(1/2)=2 ⇒A=(5/6) ⇒T_n =(1/2)(5×3^(n−1) −1)

$${let}\:\boldsymbol{{T}}_{\boldsymbol{{n}}} =\boldsymbol{{Ap}}^{\boldsymbol{{n}}} +\boldsymbol{{C}} \\ $$$$\boldsymbol{{T}}_{\boldsymbol{{n}}} =\mathrm{2}\boldsymbol{{T}}_{\boldsymbol{{n}}−\mathrm{1}} +\mathrm{1} \\ $$$${Ap}^{{n}} +{C}−\mathrm{2}{Ap}^{{n}−\mathrm{1}} −\mathrm{2}{C}−\mathrm{1}=\mathrm{0} \\ $$$${A}\left({p}−\mathrm{2}\right){p}^{{n}−\mathrm{1}} −\left({C}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{p}=\mathrm{2} \\ $$$$\Rightarrow{C}=−\mathrm{1} \\ $$$$\Rightarrow{T}_{{n}} ={A}×\mathrm{2}^{{n}} −\mathrm{1} \\ $$$${T}_{\mathrm{1}} ={A}×\mathrm{2}−\mathrm{1}=\mathrm{2} \\ $$$$\Rightarrow{A}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\Rightarrow{T}_{{n}} =\mathrm{3}×\mathrm{2}^{{n}−\mathrm{1}} −\mathrm{1} \\ $$$$ \\ $$$${if}\:{the}\:{question}\:{is}\:\boldsymbol{{T}}_{\boldsymbol{{n}}} =\mathrm{3}\boldsymbol{{T}}_{\boldsymbol{{n}}−\mathrm{1}} +\mathrm{1} \\ $$$${Ap}^{{n}} +{C}−\mathrm{3}{Ap}^{{n}−\mathrm{1}} −\mathrm{3}{C}−\mathrm{1}=\mathrm{0} \\ $$$${A}\left({p}−\mathrm{3}\right){p}^{{n}−\mathrm{1}} −\left(\mathrm{2}{C}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{p}=\mathrm{3} \\ $$$$\Rightarrow{C}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{T}_{{n}} ={A}×\mathrm{3}^{{n}} −\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{T}_{\mathrm{1}} ={A}×\mathrm{3}−\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{2} \\ $$$$\Rightarrow{A}=\frac{\mathrm{5}}{\mathrm{6}} \\ $$$$\Rightarrow{T}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{5}×\mathrm{3}^{{n}−\mathrm{1}} −\mathrm{1}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com