
Question Number 56141 by gunawan last updated on 11/Mar/19
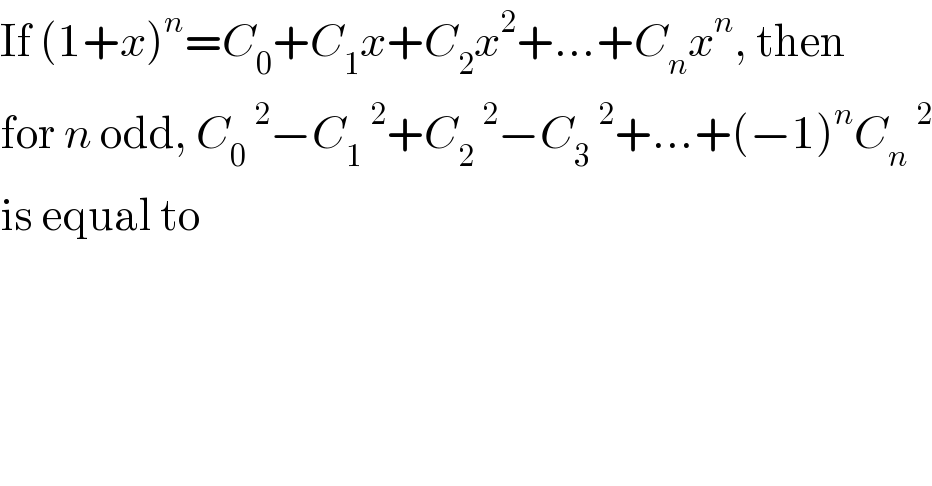
$$\mathrm{If}\:\left(\mathrm{1}+{x}\right)^{{n}} ={C}_{\mathrm{0}} +{C}_{\mathrm{1}} {x}+{C}_{\mathrm{2}} {x}^{\mathrm{2}} +...+{C}_{{n}} {x}^{{n}} ,\:\mathrm{then} \\ $$$$\mathrm{for}\:{n}\:\mathrm{odd},\:{C}_{\mathrm{0}} \:^{\mathrm{2}} −{C}_{\mathrm{1}} \:^{\mathrm{2}} +{C}_{\mathrm{2}} \:^{\mathrm{2}} −{C}_{\mathrm{3}} \:^{\mathrm{2}} +...+\left(−\mathrm{1}\right)^{{n}} {C}_{{n}} \:^{\mathrm{2}} \\ $$$$\mathrm{is}\:\mathrm{equal}\:\mathrm{to} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 11/Mar/19
![(1+x)^n =c_0 +c_1 x+c_2 x^2 +...+c_n x^n (1−(1/x))^n =c_0 −c_1 ×(1/x)+c_2 ×(1/x^2 )+...+(−1)^n ×(1/x^n ) {(1+x)(1−(1/x))}^n ={1−(1/x)+x−1}^n =(x−(1/x))^n let r+1 th term contains x^0 [x independent term] nc_r (x)^(n−r) (((−1)/x))^r ((n!)/(r!(n−r)!))×x^(n−r) ×(−1)^r ×(1/x^r ) ((n!)/(r!(n−r)!))×(−1)^r ×x^(n−2r) so n−2r=0 →r=(n/2) hence c_0 ^2 −c_1 ^2 +c_2 ^2 ....+(−1)^n c_n ^2 =((n!)/(((n/2))!((n/2))!))×(−1)^(n/2)](Q56160.png)
$$\left(\mathrm{1}+{x}\right)^{{n}} ={c}_{\mathrm{0}} +{c}_{\mathrm{1}} {x}+{c}_{\mathrm{2}} {x}^{\mathrm{2}} +...+{c}_{{n}} {x}^{{n}} \\ $$$$\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)^{{n}} ={c}_{\mathrm{0}} −{c}_{\mathrm{1}} ×\frac{\mathrm{1}}{{x}}+{c}_{\mathrm{2}} ×\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+...+\left(−\mathrm{1}\right)^{{n}} ×\frac{\mathrm{1}}{{x}^{{n}} } \\ $$$$\left\{\left(\mathrm{1}+{x}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)\right\}^{{n}} \\ $$$$=\left\{\mathrm{1}−\frac{\mathrm{1}}{{x}}+{x}−\mathrm{1}\right\}^{{n}} \\ $$$$=\left({x}−\frac{\mathrm{1}}{{x}}\right)^{{n}} \\ $$$${let}\:{r}+\mathrm{1}\:{th}\:{term}\:{contains}\:{x}^{\mathrm{0}} \left[{x}\:{independent}\:{term}\right] \\ $$$${nc}_{{r}} \left({x}\right)^{{n}−{r}} \left(\frac{−\mathrm{1}}{{x}}\right)^{{r}} \\ $$$$\frac{{n}!}{{r}!\left({n}−{r}\right)!}×{x}^{{n}−{r}} ×\left(−\mathrm{1}\right)^{{r}} ×\frac{\mathrm{1}}{{x}^{{r}} } \\ $$$$\frac{{n}!}{{r}!\left({n}−{r}\right)!}×\left(−\mathrm{1}\right)^{{r}} ×{x}^{{n}−\mathrm{2}{r}} \\ $$$${so}\:{n}−\mathrm{2}{r}=\mathrm{0}\:\:\:\rightarrow{r}=\frac{{n}}{\mathrm{2}} \\ $$$${hence} \\ $$$${c}_{\mathrm{0}} ^{\mathrm{2}} −{c}_{\mathrm{1}} ^{\mathrm{2}} +{c}_{\mathrm{2}} ^{\mathrm{2}} \:....+\left(−\mathrm{1}\right)^{{n}} {c}_{{n}} ^{\mathrm{2}} =\frac{{n}!}{\left(\frac{{n}}{\mathrm{2}}\right)!\left(\frac{{n}}{\mathrm{2}}\right)!}×\left(−\mathrm{1}\right)^{\frac{{n}}{\mathrm{2}}} \\ $$$$ \\ $$
