
Question and Answers Forum
Question Number 56144 by gunawan last updated on 11/Mar/19
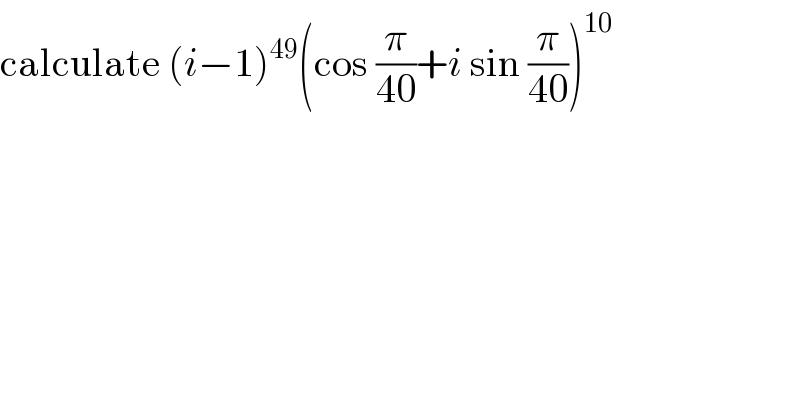
Answered by Smail last updated on 11/Mar/19
![(i−1)^(49) =[(√2)(((√2)/2)−i((√2)/2))]^(49) =(√2^(49) )(e^(i(π/4)) )^(49) =2^(24) (√2)e^(i((49π)/4)) =2^(24) (√2)e^(i((π/4)+12π)) =2^(24) (√2)e^(i(π/4)) (cos(π/(40))+isin(π/(40)))^(10) =(e^(i(π/(40))) )^(10) =e^(i(π/4)) (i−1)^(49) (cos(π/(40))+isin(π/(40)))^(10) =(2^(24) (√2)e^(i(π/4)) )e^(i(π/4)) =2^(24) (√2)e^(i(π/2)) =2^(24) (√2)i](Q56153.png)
| ||
Question and Answers Forum | ||
Question Number 56144 by gunawan last updated on 11/Mar/19 | ||
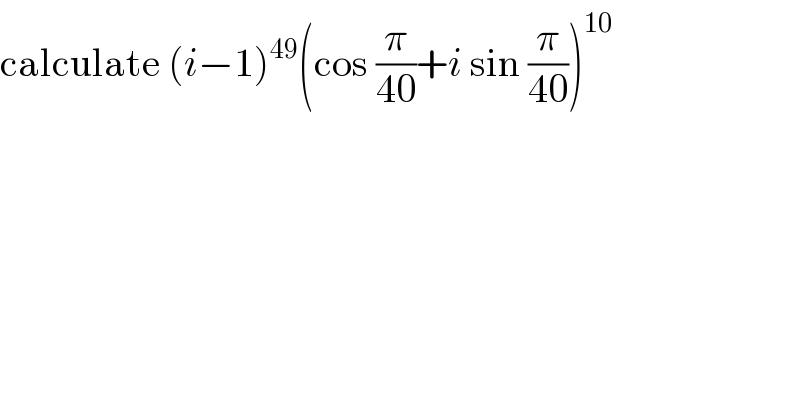 | ||
Answered by Smail last updated on 11/Mar/19 | ||
![(i−1)^(49) =[(√2)(((√2)/2)−i((√2)/2))]^(49) =(√2^(49) )(e^(i(π/4)) )^(49) =2^(24) (√2)e^(i((49π)/4)) =2^(24) (√2)e^(i((π/4)+12π)) =2^(24) (√2)e^(i(π/4)) (cos(π/(40))+isin(π/(40)))^(10) =(e^(i(π/(40))) )^(10) =e^(i(π/4)) (i−1)^(49) (cos(π/(40))+isin(π/(40)))^(10) =(2^(24) (√2)e^(i(π/4)) )e^(i(π/4)) =2^(24) (√2)e^(i(π/2)) =2^(24) (√2)i](Q56153.png) | ||
| ||