Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 56146 by gunawan last updated on 11/Mar/19

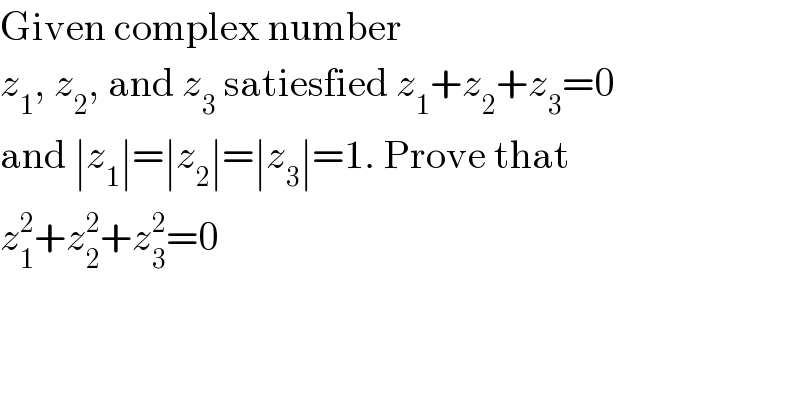
Given complex number z_1 , z_2 , and z_3 satiesfied z_1 +z_2 +z_3 =0 and ∣z_1 ∣=∣z_2 ∣=∣z_3 ∣=1. Prove that z_1 ^2 +z_2 ^2 +z_3 ^2 =0

$$\mathrm{Given}\:\mathrm{complex}\:\mathrm{number} \\ $$$${z}_{\mathrm{1}} ,\:{z}_{\mathrm{2}} ,\:\mathrm{and}\:{z}_{\mathrm{3}} \:\mathrm{satiesfied}\:{z}_{\mathrm{1}} +{z}_{\mathrm{2}} +{z}_{\mathrm{3}} =\mathrm{0} \\ $$$$\mathrm{and}\:\mid{z}_{\mathrm{1}} \mid=\mid{z}_{\mathrm{2}} \mid=\mid{z}_{\mathrm{3}} \mid=\mathrm{1}.\:\mathrm{Prove}\:\mathrm{that} \\ $$$${z}_{\mathrm{1}} ^{\mathrm{2}} +{z}_{\mathrm{2}} ^{\mathrm{2}} +{z}_{\mathrm{3}} ^{\mathrm{2}} =\mathrm{0} \\ $$

Commented by MJS last updated on 11/Mar/19

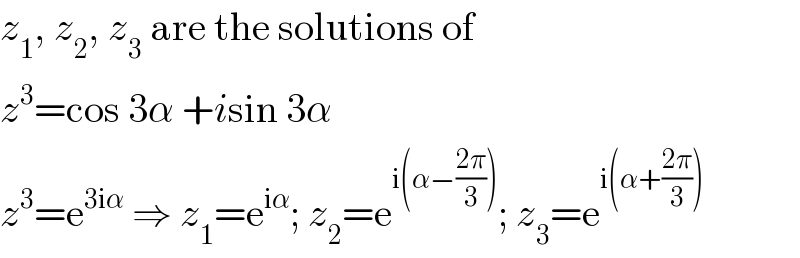
z_1 , z_2 , z_3 are the solutions of z^3 =cos 3α +isin 3α z^3 =e^(3iα) ⇒ z_1 =e^(iα) ; z_2 =e^(i(α−((2π)/3))) ; z_3 =e^(i(α+((2π)/3)))

$${z}_{\mathrm{1}} ,\:{z}_{\mathrm{2}} ,\:{z}_{\mathrm{3}} \:\mathrm{are}\:\mathrm{the}\:\mathrm{solutions}\:\mathrm{of} \\ $$$${z}^{\mathrm{3}} =\mathrm{cos}\:\mathrm{3}\alpha\:+{i}\mathrm{sin}\:\mathrm{3}\alpha \\ $$$${z}^{\mathrm{3}} =\mathrm{e}^{\mathrm{3i}\alpha} \:\Rightarrow\:{z}_{\mathrm{1}} =\mathrm{e}^{\mathrm{i}\alpha} ;\:{z}_{\mathrm{2}} =\mathrm{e}^{\mathrm{i}\left(\alpha−\frac{\mathrm{2}\pi}{\mathrm{3}}\right)} ;\:{z}_{\mathrm{3}} =\mathrm{e}^{\mathrm{i}\left(\alpha+\frac{\mathrm{2}\pi}{\mathrm{3}}\right)} \\ $$

Answered by MJS last updated on 11/Mar/19

we can choose z_3 =1+0i z_1 =a+bi z_2 =c+di (1) a+c+1=0 (2) b+d=0 (3) a^2 +b^2 =1 (4) c^2 +d^2 =1 (1) ⇒ c=−(a+1) (2) ⇒ d=−b (3) a^2 +b^2 =1 (4) a^2 +2a+b^2 +1=1 (4)−(3) 2a+1=0 ⇒ a=−(1/2) ⇒ c=−(1/2) ⇒ b^2 =(3/4) ⇒ b=±((√3)/2) ⇒ d=∓((√3)/2) ⇒ z_1 =−(1/2)±((√3)/2); z_2 =−(1/2)∓((√3)/2) ⇒ z_1 ^2 =z_2 ; z_2 ^2 =z_1 ⇒ z_1 ^2 +z_2 ^2 +z_3 ^2 =0 we have got the roots of unity ⇒ for any given z_3 =cos α +isin α we get z_(1, 2) =cos (α±((2π)/3)) +isin (α±((2π)/3)) because it′s just a rotation by α the sum of the squares is zero which can be shown by adding them and using trigonometric formulas for additions etc.

$$\mathrm{we}\:\mathrm{can}\:\mathrm{choose}\:{z}_{\mathrm{3}} =\mathrm{1}+\mathrm{0i} \\ $$$${z}_{\mathrm{1}} ={a}+{b}\mathrm{i} \\ $$$${z}_{\mathrm{2}} ={c}+{d}\mathrm{i} \\ $$$$\left(\mathrm{1}\right)\:\:{a}+{c}+\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{2}\right)\:\:{b}+{d}=\mathrm{0} \\ $$$$\left(\mathrm{3}\right)\:\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{1} \\ $$$$\left(\mathrm{4}\right)\:\:{c}^{\mathrm{2}} +{d}^{\mathrm{2}} =\mathrm{1} \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:\Rightarrow\:{c}=−\left({a}+\mathrm{1}\right) \\ $$$$\left(\mathrm{2}\right)\:\Rightarrow\:{d}=−{b} \\ $$$$\left(\mathrm{3}\right)\:\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{1} \\ $$$$\left(\mathrm{4}\right)\:\:{a}^{\mathrm{2}} +\mathrm{2}{a}+{b}^{\mathrm{2}} +\mathrm{1}=\mathrm{1} \\ $$$$\left(\mathrm{4}\right)−\left(\mathrm{3}\right)\:\:\mathrm{2}{a}+\mathrm{1}=\mathrm{0}\:\Rightarrow\:{a}=−\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\:{c}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\:{b}^{\mathrm{2}} =\frac{\mathrm{3}}{\mathrm{4}}\:\Rightarrow\:{b}=\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\Rightarrow\:{d}=\mp\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\Rightarrow\:{z}_{\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}};\:{z}_{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{2}}\mp\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\Rightarrow\:{z}_{\mathrm{1}} ^{\mathrm{2}} ={z}_{\mathrm{2}} ;\:{z}_{\mathrm{2}} ^{\mathrm{2}} ={z}_{\mathrm{1}} \:\Rightarrow\:{z}_{\mathrm{1}} ^{\mathrm{2}} +{z}_{\mathrm{2}} ^{\mathrm{2}} +{z}_{\mathrm{3}} ^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{got}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{unity}\:\Rightarrow\:\mathrm{for}\:\mathrm{any} \\ $$$$\mathrm{given}\:{z}_{\mathrm{3}} =\mathrm{cos}\:\alpha\:+{i}\mathrm{sin}\:\alpha\:\mathrm{we}\:\mathrm{get} \\ $$$${z}_{\mathrm{1},\:\mathrm{2}} =\mathrm{cos}\:\left(\alpha\pm\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\:+{i}\mathrm{sin}\:\left(\alpha\pm\frac{\mathrm{2}\pi}{\mathrm{3}}\right) \\ $$$$\mathrm{because}\:\mathrm{it}'\mathrm{s}\:\mathrm{just}\:\mathrm{a}\:\mathrm{rotation}\:\mathrm{by}\:\alpha \\ $$$$\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{squares}\:\mathrm{is}\:\mathrm{zero}\:\mathrm{which}\:\mathrm{can}\:\mathrm{be} \\ $$$$\mathrm{shown}\:\mathrm{by}\:\mathrm{adding}\:\mathrm{them}\:\mathrm{and}\:\mathrm{using}\:\mathrm{trigonometric} \\ $$$$\mathrm{formulas}\:\mathrm{for}\:\mathrm{additions}\:\mathrm{etc}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com