Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 56147 by afachri last updated on 11/Mar/19

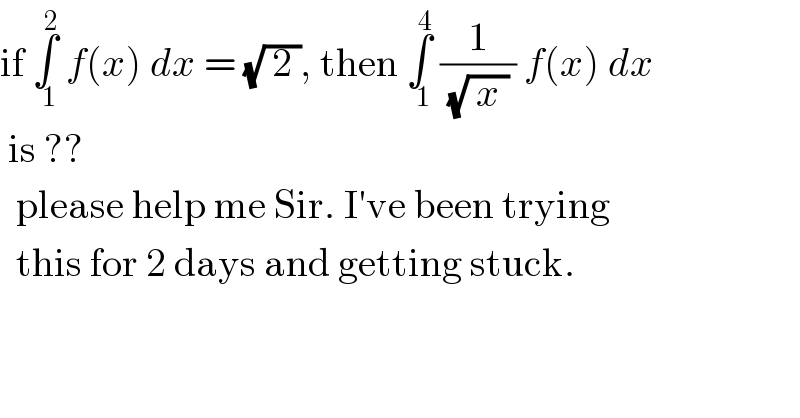
if ∫_( 1) ^( 2) f(x) dx = (√( 2 )), then ∫_( 1) ^( 4) (1/((√( x )) )) f(x) dx is ?? please help me Sir. I′ve been trying this for 2 days and getting stuck.

$$\mathrm{if}\:\underset{\:\:\mathrm{1}} {\overset{\:\:\mathrm{2}} {\int}}\:{f}\left({x}\right)\:{dx}\:=\:\sqrt{\:\mathrm{2}\:},\:\mathrm{then}\:\underset{\:\:\mathrm{1}} {\overset{\:\:\mathrm{4}} {\int}}\:\frac{\mathrm{1}}{\sqrt{\:{x}\:}\:}\:{f}\left({x}\right)\:{dx} \\ $$$$\:\mathrm{is}\:?? \\ $$$$\:\:\mathrm{please}\:\mathrm{help}\:\mathrm{me}\:\mathrm{Sir}.\:\mathrm{I}'\mathrm{ve}\:\mathrm{been}\:\mathrm{trying} \\ $$$$\:\:\mathrm{this}\:\mathrm{for}\:\mathrm{2}\:\mathrm{days}\:\mathrm{and}\:\mathrm{getting}\:\mathrm{stuck}. \\ $$$$ \\ $$$$ \\ $$

Commented by 121194 last updated on 11/Mar/19

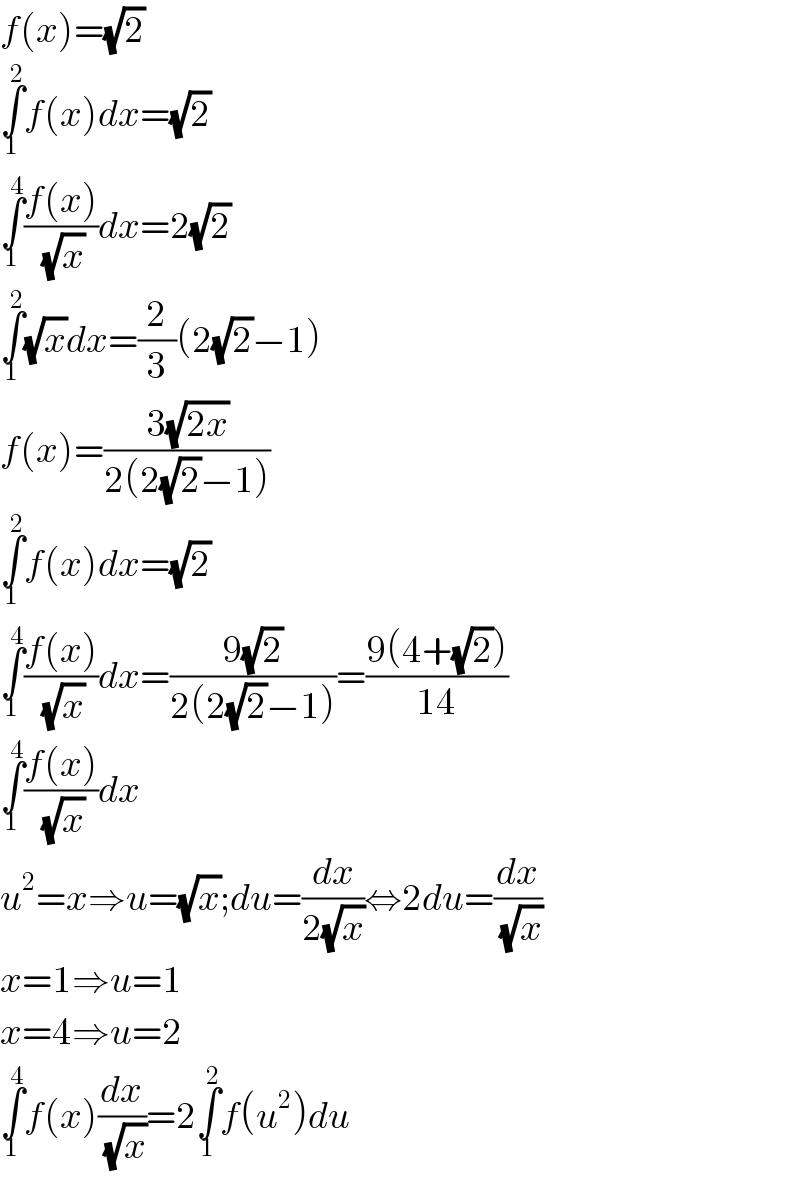
f(x)=(√2) ∫_1 ^2 f(x)dx=(√2) ∫_1 ^4 ((f(x))/(√x))dx=2(√2) ∫_1 ^2 (√x)dx=(2/3)(2(√2)−1) f(x)=((3(√(2x)))/(2(2(√2)−1))) ∫_1 ^2 f(x)dx=(√2) ∫_1 ^4 ((f(x))/(√x))dx=((9(√2))/(2(2(√2)−1)))=((9(4+(√2)))/(14)) ∫_1 ^4 ((f(x))/(√x))dx u^2 =x⇒u=(√x);du=(dx/(2(√x)))⇔2du=(dx/(√x)) x=1⇒u=1 x=4⇒u=2 ∫_1 ^4 f(x)(dx/(√x))=2∫_1 ^2 f(u^2 )du

$${f}\left({x}\right)=\sqrt{\mathrm{2}} \\ $$$$\underset{\mathrm{1}} {\overset{\mathrm{2}} {\int}}{f}\left({x}\right){dx}=\sqrt{\mathrm{2}} \\ $$$$\underset{\mathrm{1}} {\overset{\mathrm{4}} {\int}}\frac{{f}\left({x}\right)}{\sqrt{{x}}}{dx}=\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\underset{\mathrm{1}} {\overset{\mathrm{2}} {\int}}\sqrt{{x}}{dx}=\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{1}\right) \\ $$$${f}\left({x}\right)=\frac{\mathrm{3}\sqrt{\mathrm{2}{x}}}{\mathrm{2}\left(\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{1}\right)} \\ $$$$\underset{\mathrm{1}} {\overset{\mathrm{2}} {\int}}{f}\left({x}\right){dx}=\sqrt{\mathrm{2}} \\ $$$$\underset{\mathrm{1}} {\overset{\mathrm{4}} {\int}}\frac{{f}\left({x}\right)}{\sqrt{{x}}}{dx}=\frac{\mathrm{9}\sqrt{\mathrm{2}}}{\mathrm{2}\left(\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{1}\right)}=\frac{\mathrm{9}\left(\mathrm{4}+\sqrt{\mathrm{2}}\right)}{\mathrm{14}} \\ $$$$\underset{\mathrm{1}} {\overset{\mathrm{4}} {\int}}\frac{{f}\left({x}\right)}{\sqrt{{x}}}{dx} \\ $$$${u}^{\mathrm{2}} ={x}\Rightarrow{u}=\sqrt{{x}};{du}=\frac{{dx}}{\mathrm{2}\sqrt{{x}}}\Leftrightarrow\mathrm{2}{du}=\frac{{dx}}{\sqrt{{x}}} \\ $$$${x}=\mathrm{1}\Rightarrow{u}=\mathrm{1} \\ $$$${x}=\mathrm{4}\Rightarrow{u}=\mathrm{2} \\ $$$$\underset{\mathrm{1}} {\overset{\mathrm{4}} {\int}}{f}\left({x}\right)\frac{{dx}}{\sqrt{{x}}}=\mathrm{2}\underset{\mathrm{1}} {\overset{\mathrm{2}} {\int}}{f}\left({u}^{\mathrm{2}} \right){du} \\ $$

Commented by 121194 last updated on 11/Mar/19

are you sure this question is right?

$$\mathrm{are}\:\mathrm{you}\:\mathrm{sure}\:\mathrm{this}\:\mathrm{question}\:\mathrm{is}\:\mathrm{right}? \\ $$

Commented by afachri last updated on 11/Mar/19

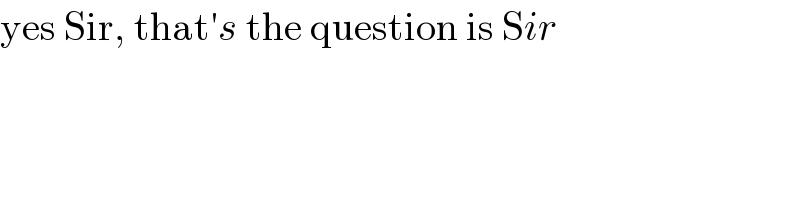
yes Sir, that′s the question is Sir

$$\mathrm{yes}\:\mathrm{Sir},\:\mathrm{that}'{s}\:\mathrm{the}\:\mathrm{question}\:\mathrm{is}\:\mathrm{S}{ir} \\ $$

Commented by afachri last updated on 11/Mar/19

pardon me Sir. I don′t undersrand your solution. Please rewrite it clearly Sir.

$${pardon}\:{me}\:{Sir}.\:{I}\:{don}'{t}\:{undersrand} \\ $$$${your}\:{solution}.\:{Please}\:{rewrite}\:{it} \\ $$$${clearly}\:{Sir}. \\ $$

Commented by 121194 last updated on 11/Mar/19

wierd, i don′t think that condition is enought to determinate the other. because unless i made a typo, there2 diferet function such ∫_1 ^2 f(x)dx=(√2), but ∫_1 ^4 ((f(x))/(√x))dx gives diferent values also given g:[1,4]→R integable on that domain, you can always build a solution to it with f(x)=(((√2)g(x))/(∫_1 ^2 g(x)dx));∫_1 ^2 g(x)dx≠0

$$\mathrm{wierd},\:\mathrm{i}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{that}\:\mathrm{condition}\:\mathrm{is}\:\mathrm{enought}\:\mathrm{to} \\ $$$$\mathrm{determinate}\:\mathrm{the}\:\mathrm{other}. \\ $$$$\mathrm{because}\:\mathrm{unless}\:\mathrm{i}\:\mathrm{made}\:\mathrm{a}\:\mathrm{typo},\:\mathrm{there2}\:\mathrm{diferet}\:\mathrm{function} \\ $$$$\mathrm{such}\:\underset{\mathrm{1}} {\overset{\mathrm{2}} {\int}}{f}\left({x}\right){dx}=\sqrt{\mathrm{2}},\:\mathrm{but}\:\underset{\mathrm{1}} {\overset{\mathrm{4}} {\int}}\frac{{f}\left({x}\right)}{\sqrt{{x}}}{dx}\:\mathrm{gives}\:\mathrm{diferent}\:\mathrm{values} \\ $$$$\mathrm{also}\:\mathrm{given}\:{g}:\left[\mathrm{1},\mathrm{4}\right]\rightarrow\mathbb{R}\:\mathrm{integable}\:\mathrm{on}\:\mathrm{that}\:\mathrm{domain}, \\ $$$$\mathrm{you}\:\mathrm{can}\:\mathrm{always}\:\mathrm{build}\:\mathrm{a}\:\mathrm{solution}\:\mathrm{to}\:\mathrm{it}\:\mathrm{with} \\ $$$${f}\left({x}\right)=\frac{\sqrt{\mathrm{2}}{g}\left({x}\right)}{\underset{\mathrm{1}} {\overset{\mathrm{2}} {\int}}{g}\left({x}\right){dx}};\underset{\mathrm{1}} {\overset{\mathrm{2}} {\int}}{g}\left({x}\right){dx}\neq\mathrm{0} \\ $$

Commented by prakash jain last updated on 12/Mar/19

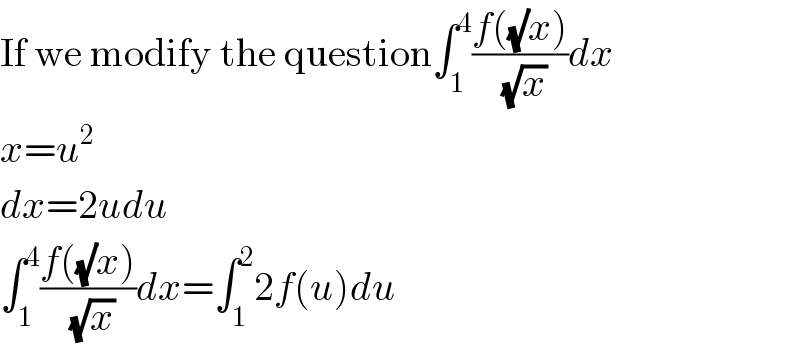
If we modify the question∫_1 ^4 ((f((√)x))/(√x))dx x=u^2 dx=2udu ∫_1 ^4 ((f((√)x))/(√x))dx=∫_1 ^2 2f(u)du

$$\mathrm{If}\:\mathrm{we}\:\mathrm{modify}\:\mathrm{the}\:\mathrm{question}\int_{\mathrm{1}} ^{\mathrm{4}} \frac{{f}\left(\sqrt{}{x}\right)}{\sqrt{{x}}}{dx} \\ $$$${x}={u}^{\mathrm{2}} \\ $$$${dx}=\mathrm{2}{udu} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{4}} \frac{{f}\left(\sqrt{}{x}\right)}{\sqrt{{x}}}{dx}=\int_{\mathrm{1}} ^{\mathrm{2}} \mathrm{2}{f}\left({u}\right){du} \\ $$

Answered by MJS last updated on 11/Mar/19

if we don′t know the nature of f(x) we can′t solve. the number of functions satisfying the 1^(st) condition is ∞

$$\mathrm{if}\:\mathrm{we}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{the}\:\mathrm{nature}\:\mathrm{of}\:{f}\left({x}\right)\:\mathrm{we}\:\mathrm{can}'\mathrm{t} \\ $$$$\mathrm{solve}.\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{functions}\:\mathrm{satisfying}\:\mathrm{the} \\ $$$$\mathrm{1}^{\mathrm{st}} \:\mathrm{condition}\:\mathrm{is}\:\infty \\ $$

Commented by MJS last updated on 11/Mar/19

even if f(x) is linear it′s not determined: f(x)=ax+b ∫_1 ^2 f(x)dx=((3a)/2)+b=(√2) ⇒ b=(√2)−((3a)/2) f(x)=ax+(√2)−((3a)/2); a∈R ∫_1 ^4 ((f(x))/(√x))dx=((5a)/3)+2(√2); a∈R if b=0 ⇒ a=((2(√2))/3) ⇒ ∫_1 ^4 ((f(x))/(√x))dx=((28(√2))/9) if a=0 ⇒ b=(√2) ⇒ ∫_1 ^4 ((f(x))/(√x))dx=2(√2) ...

$$\mathrm{even}\:\mathrm{if}\:{f}\left({x}\right)\:\mathrm{is}\:\mathrm{linear}\:\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{determined}: \\ $$$${f}\left({x}\right)={ax}+{b} \\ $$$$\underset{\mathrm{1}} {\overset{\mathrm{2}} {\int}}{f}\left({x}\right){dx}=\frac{\mathrm{3}{a}}{\mathrm{2}}+{b}=\sqrt{\mathrm{2}}\:\Rightarrow\:{b}=\sqrt{\mathrm{2}}−\frac{\mathrm{3}{a}}{\mathrm{2}} \\ $$$${f}\left({x}\right)={ax}+\sqrt{\mathrm{2}}−\frac{\mathrm{3}{a}}{\mathrm{2}};\:{a}\in\mathbb{R} \\ $$$$\underset{\mathrm{1}} {\overset{\mathrm{4}} {\int}}\frac{{f}\left({x}\right)}{\sqrt{{x}}}{dx}=\frac{\mathrm{5}{a}}{\mathrm{3}}+\mathrm{2}\sqrt{\mathrm{2}};\:{a}\in\mathbb{R} \\ $$$$ \\ $$$$\mathrm{if}\:{b}=\mathrm{0}\:\Rightarrow\:{a}=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\:\Rightarrow\:\underset{\mathrm{1}} {\overset{\mathrm{4}} {\int}}\frac{{f}\left({x}\right)}{\sqrt{{x}}}{dx}=\frac{\mathrm{28}\sqrt{\mathrm{2}}}{\mathrm{9}} \\ $$$$\mathrm{if}\:{a}=\mathrm{0}\:\Rightarrow\:{b}=\sqrt{\mathrm{2}}\:\Rightarrow\:\underset{\mathrm{1}} {\overset{\mathrm{4}} {\int}}\frac{{f}\left({x}\right)}{\sqrt{{x}}}{dx}=\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$... \\ $$

Commented by afachri last updated on 11/Mar/19

thank you for all of You Sir. that was i thinking before. how to or is that any possible to do to find the real f(x)

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{for}\:\mathrm{all}\:\mathrm{of}\:{You}\:\mathrm{S}{ir}. \\ $$$$\mathrm{that}\:\mathrm{was}\:\mathrm{i}\:\mathrm{thinking}\:\mathrm{before}.\:\mathrm{how} \\ $$$$\mathrm{to}\:\mathrm{or}\:\mathrm{is}\:\mathrm{that}\:\mathrm{any}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{do}\:\mathrm{to} \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{real}\:{f}\left({x}\right)\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com