Question Number 56229 by Hassen_Timol last updated on 12/Mar/19
$$\mathrm{How}\:\mathrm{can}\:\mathrm{you}\:\mathrm{prove}\:\left(\mathrm{not}\:\mathrm{geometrically}\right) \\ $$$$\mathrm{the}\:\mathrm{following}? \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\underset{{k}\:=\:\mathrm{0}} {\overset{{n}} {\sum}}{k}\:\:=\:\:\frac{\:{n}\:\left(\:{n}\:+\:\mathrm{1}\:\right)\:}{\mathrm{2}} \\ $$$$ \\ $$
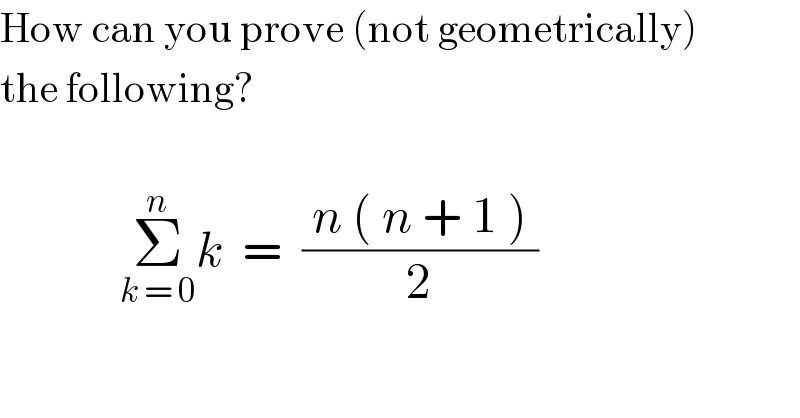
Commented by Kunal12588 last updated on 12/Mar/19
$${Can}\:{I}\:{use}\:{Aritmetic}\:{Progression}\:{AP}\:{sir}. \\ $$
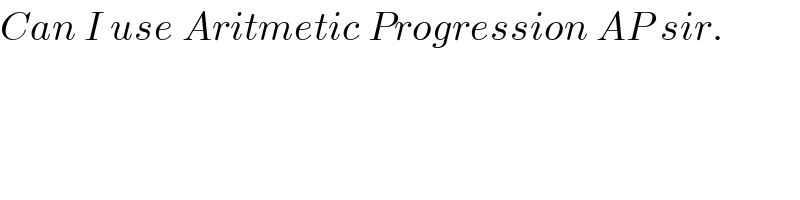
Commented by Hassen_Timol last updated on 12/Mar/19
$${yes}\:{Sir}\:{please} \\ $$
Commented by Kunal12588 last updated on 12/Mar/19
![Σ_(k=0) ^n k=0+1+2+3+4+...+n let us write the terms 0,1,2,3,4,5,6,7,...,n above sequence is in AP where a=0, d=1 S_r =(r/2)[2a+(r−1)d] ∴S_(n+1) =(((n+1))/2)[2×0+((n+1)−1)(1)] ⇒S_(n+1) =((n+1)/2)(0+n×1)=((n(n+1))/2)](Q56240.png)
$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{k}=\mathrm{0}+\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+...+{n} \\ $$$${let}\:{us}\:{write}\:{the}\:{terms} \\ $$$$\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5},\mathrm{6},\mathrm{7},...,{n} \\ $$$${above}\:{sequence}\:{is}\:{in}\:{AP} \\ $$$${where}\:{a}=\mathrm{0},\:{d}=\mathrm{1} \\ $$$${S}_{{r}} =\frac{{r}}{\mathrm{2}}\left[\mathrm{2}{a}+\left({r}−\mathrm{1}\right){d}\right] \\ $$$$\therefore{S}_{{n}+\mathrm{1}} =\frac{\left({n}+\mathrm{1}\right)}{\mathrm{2}}\left[\mathrm{2}×\mathrm{0}+\left(\left({n}+\mathrm{1}\right)−\mathrm{1}\right)\left(\mathrm{1}\right)\right] \\ $$$$\Rightarrow{S}_{{n}+\mathrm{1}} =\frac{{n}+\mathrm{1}}{\mathrm{2}}\left(\mathrm{0}+{n}×\mathrm{1}\right)=\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}} \\ $$
Commented by maxmathsup by imad last updated on 13/Mar/19
![solution by polynome method let p(x)=((x(x−1))/2) we have for all x from R p(x+1)−p(x)=(((x+1)x)/2) −((x(x−1))/2) =((x^2 +x −x^2 +x)/2) =x ⇒ ∀ k∈[[1,n]] p(k+1)−p(k) =k ⇒Σ_(k=1) ^n {p(k+1)−p(k)}=Σ_(k=1) ^n k ⇒ Σ_(k=1) ^n k =p(2)−p(1)+p(3)−p(2)+....+p(n+1)−p(n)=p(n+1)−p(1) =((n(n+1))/2) −0 ⇒ Σ_(k=1) ^n k =((n(n+1))/2) .](Q56312.png)
$${solution}\:{by}\:{polynome}\:{method}\:{let}\:{p}\left({x}\right)=\frac{{x}\left({x}−\mathrm{1}\right)}{\mathrm{2}}\:{we}\:{have}\:{for}\:{all}\:{x}\:{from}\:{R} \\ $$$${p}\left({x}+\mathrm{1}\right)−{p}\left({x}\right)=\frac{\left({x}+\mathrm{1}\right){x}}{\mathrm{2}}\:−\frac{{x}\left({x}−\mathrm{1}\right)}{\mathrm{2}}\:=\frac{{x}^{\mathrm{2}} +{x}\:−{x}^{\mathrm{2}} \:+{x}}{\mathrm{2}}\:={x}\:\Rightarrow \\ $$$$\forall\:{k}\in\left[\left[\mathrm{1},{n}\right]\right]\:{p}\left({k}+\mathrm{1}\right)−{p}\left({k}\right)\:={k}\:\Rightarrow\sum_{{k}=\mathrm{1}} ^{{n}} \left\{{p}\left({k}+\mathrm{1}\right)−{p}\left({k}\right)\right\}=\sum_{{k}=\mathrm{1}} ^{{n}} \:{k}\:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} {k}\:={p}\left(\mathrm{2}\right)−{p}\left(\mathrm{1}\right)+{p}\left(\mathrm{3}\right)−{p}\left(\mathrm{2}\right)+....+{p}\left({n}+\mathrm{1}\right)−{p}\left({n}\right)={p}\left({n}+\mathrm{1}\right)−{p}\left(\mathrm{1}\right) \\ $$$$=\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\:−\mathrm{0}\:\Rightarrow\:\sum_{{k}=\mathrm{1}} ^{{n}} {k}\:=\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\:. \\ $$$$ \\ $$
Answered by Prithwish sen last updated on 12/Mar/19
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{k}\:=\:\mathrm{1}+\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:+\:\:\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:+............+\left(\mathrm{n}−\mathrm{2}\right)+\left(\mathrm{n}−\mathrm{1}\right)+\mathrm{n} \\ $$$$\:\mathrm{again}\:\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{k}\:=\:\mathrm{n}+\left(\mathrm{n}−\mathrm{1}\right)+\left(\mathrm{n}−\mathrm{2}\right)\:+.............+\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:\:\:+\:\:\:\mathrm{2}\:\:\:\:\:\:\:+\mathrm{1}\:\:\:\:\:\: \\ $$$$\mathrm{adding}\:\mathrm{2}\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}=\:\left(\mathrm{n}+\mathrm{1}\right)+\left(\mathrm{n}+\mathrm{1}\right)+....\mathrm{upto}\:\mathrm{n}\:\mathrm{times} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\therefore\:\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}=\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2}}\:\:\:\mathrm{proved} \\ $$
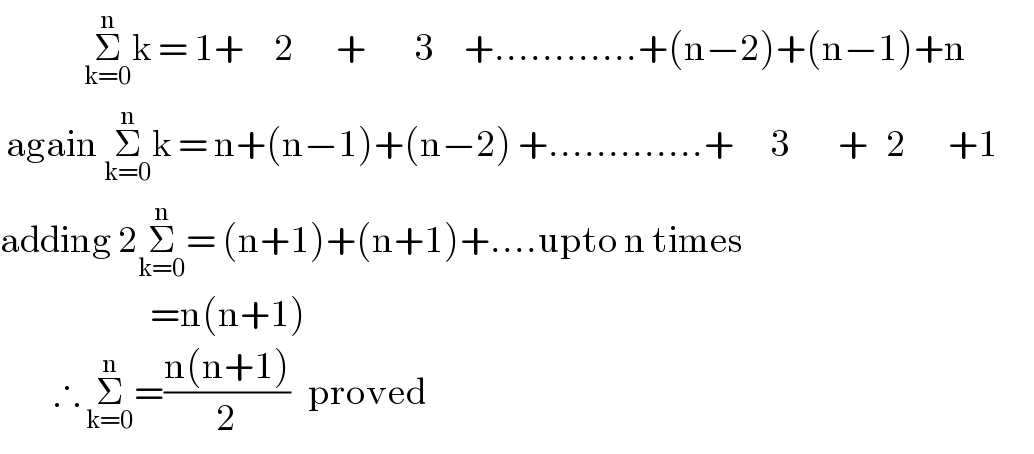
Commented by Hassen_Timol last updated on 12/Mar/19
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you} \\ $$
Answered by Kunal12588 last updated on 12/Mar/19
![S_(n+1) =Σ_(k = 0) ^n k=0+1+2+3+4+...+n (1) There are (n+1) terms in above series. Reversing S_n ∵ addition follows commutive property it does not effect the S_n S_(n+1) =n+(n−1)+(n−2)+...+0 (2) adding corresponding terms of (1) and (2) 2S_(n+1) =(0+n)+[1+(n−1)]+[2+(n−2)]+..+(n+0) there are (n+1) brackets as you can see every bracket will give us ′n′ 2S_(n+1) =n+n+n+n+...(n+1) terms 2S_(n+1) =n(n+1) S_(n+1) =((n(n+1))/2)](Q56235.png)
$$ \\ $$$${S}_{{n}+\mathrm{1}} =\underset{{k}\:=\:\mathrm{0}} {\overset{{n}} {\sum}}{k}=\mathrm{0}+\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+...+{n}\:\:\:\:\:\:\:\:\left(\mathrm{1}\right) \\ $$$${There}\:{are}\:\left({n}+\mathrm{1}\right)\:{terms}\:{in}\:{above}\:{series}. \\ $$$${Reversing}\:\:{S}_{{n}} \:\because\:{addition}\:{follows}\:{commutive} \\ $$$${property}\:{it}\:{does}\:{not}\:{effect}\:{the}\:{S}_{{n}} \\ $$$${S}_{{n}+\mathrm{1}} ={n}+\left({n}−\mathrm{1}\right)+\left({n}−\mathrm{2}\right)+...+\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{2}\right) \\ $$$${adding}\:{corresponding}\:{terms}\:{of}\:\left(\mathrm{1}\right)\:{and}\:\left(\mathrm{2}\right) \\ $$$$\mathrm{2}{S}_{{n}+\mathrm{1}} =\left(\mathrm{0}+{n}\right)+\left[\mathrm{1}+\left({n}−\mathrm{1}\right)\right]+\left[\mathrm{2}+\left({n}−\mathrm{2}\right)\right]+..+\left({n}+\mathrm{0}\right) \\ $$$${there}\:{are}\:\left({n}+\mathrm{1}\right)\:{brackets} \\ $$$${as}\:{you}\:{can}\:{see}\:{every}\:{bracket}\:{will}\:{give}\:{us}\:'{n}' \\ $$$$\mathrm{2}{S}_{{n}+\mathrm{1}} ={n}+{n}+{n}+{n}+...\left({n}+\mathrm{1}\right)\:{terms} \\ $$$$\mathrm{2}{S}_{{n}+\mathrm{1}} ={n}\left({n}+\mathrm{1}\right) \\ $$$${S}_{{n}+\mathrm{1}} =\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}} \\ $$
Commented by Hassen_Timol last updated on 12/Mar/19
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you} \\ $$
Commented by Prithwish sen last updated on 12/Mar/19
$$\mathrm{this}\:\mathrm{is}\:\mathrm{correct} \\ $$
Commented by Kunal12588 last updated on 12/Mar/19
$${May}\:{God}\:{bless}\:{you}\:{too}. \\ $$$${Welcome}. \\ $$