Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 56244 by Kunal12588 last updated on 12/Mar/19

$$Is\mathrm{\infty }acomplexnumber.$$$$IfnotsowhatisIt.$$

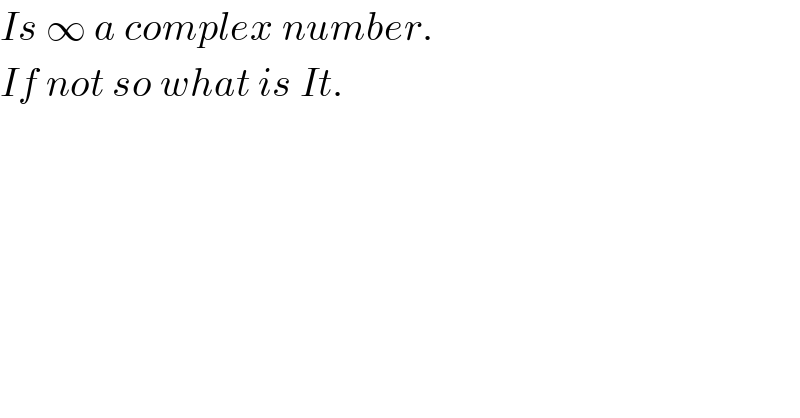
Commented by Joel578 last updated on 12/Mar/19

$$itisnotanumber$$

Commented by Kunal12588 last updated on 12/Mar/19

$$okiedokie.$$$$waitingforthenwhatitis$$$$andithoughtwecanrepresentitas\frac{1}{0}.$$$$so\frac{1}{0}isnotanumber.butbothnumerator$$$$anddenominatorarenumbers.$$

Commented by 121194 last updated on 12/Mar/19

$$\mathrm{one}\mathrm{may}\mathrm{think}\mathrm{that}\frac{1}{0}=\mathrm{\infty },\mathrm{but}\mathrm{that}\mathrm{not}\mathrm{entire}\mathrm{true}$$$$\mathrm{think}\mathrm{of}$$$$\underset{x\to 0}{\lim }\frac{1}{x}$$$$\mathrm{lets}\mathrm{aproach}\mathrm{it}2\mathrm{ways}$$$$1\to 1$$$$0.5\to 2$$$$0.1\to 10$$$$0.01\to 100$$$$0.001\to 1000$$$$asyoucanseeascloseweaproachx1/xgrow$$$$withoutanylimit,so$$$$\underset{x\to 0^{+}}{\lim }\frac{1}{x}=+\mathrm{\infty }$$$$butthatonly1path,takesthe2ndone$$$$-1\to -1$$$$-0.5\to -2$$$$-0.1\to -10$$$$-0.01\to -100$$$$asyouseeitgrowincompletopostdirection,as$$$$\underset{x\to 0^{-}}{\lim }\frac{1}{x}=-\mathrm{\infty }$$$$sincethe2limitsarediferentswe{can}^{\prime }tsaythat$$$$thelimitexistso$$$$\underset{x\to 0}{\lim }\frac{1}{x}=\nexists$$$$btwthereanyanalogousof\mathrm{\infty }tocomplex,the$$$$complexinfinite\stackrel{\sim }{\mathrm{\infty }}$$$$itbasicalya‘‘{number}^{″}withhighmodulosbut$$$$unknowargument$$

Commented by Joel578 last updated on 12/Mar/19

$$\frac{1}{0}\mathrm{is}\mathrm{actually}\mathrm{undefined}$$$$\mathrm{Now},\mathrm{let}f\left(x\right)=\frac{1}{x}$$$$\mathrm{If}\mathrm{we}\mathrm{take}x=0.00000001,f\left(x\right)=100000000$$$$\mathrm{Next},\mathrm{if}x\mathrm{getting}\mathrm{smaller},\mathrm{very}\mathrm{close}\mathrm{to}\mathrm{zero}$$$$\mathrm{then}\mathrm{our}f\left(x\right)\mathrm{is}\mathrm{getting}\mathrm{larger}$$$$\mathrm{Next},x\mathrm{now}\mathrm{is}\mathrm{very}\mathrm{very}\mathrm{very}\mathrm{smaller},\mathrm{then}$$$$\mathrm{our}f\left(x\right)\mathrm{is}\mathrm{very}\mathrm{very}\mathrm{very}\mathrm{large}.$$$$\mathrm{In}\mathrm{this}\mathrm{context},\mathrm{we}\mathrm{can}\mathrm{denote}\mathrm{this}\mathrm{as}$$$$\underset{x\to 0^{+}}{\lim }\frac{1}{x}=\frac{1}{0}=\mathrm{\infty }$$$$\mathrm{As}x\mathrm{is}\mathrm{getting}\mathrm{smaller},\mathrm{very}\mathrm{close}\mathrm{to}\mathrm{zero}$$$$\mathrm{then}\mathrm{its}\mathrm{value}\mathrm{will}\mathrm{reach}\mathrm{an}\mathrm{arbitrarily}\mathrm{large}\mathrm{number}.$$$$\mathrm{How}\mathrm{large}?\mathrm{Very}\mathrm{large}.\mathrm{And}\mathrm{we}\mathrm{denote}\mathrm{this}\mathrm{with}‘‘{\mathrm{\infty }}^{″}$$$$\mathrm{So},\mathrm{in}\mathrm{my}\mathrm{opinion}‘‘{\mathrm{\infty }}^{″}\mathrm{is}\mathrm{a}\mathrm{concept}\mathrm{to}\mathrm{describe}$$$$\mathrm{an}\mathrm{arbitrarily}\mathrm{large}\mathrm{number},\mathrm{but}\mathrm{it}{\mathrm{isn}}^{\prime }\mathrm{t}\mathrm{a}\mathrm{number}$$

Commented by Joel578 last updated on 12/Mar/19

$${\mathrm{That}}^{\prime }\mathrm{s}\mathrm{what}\mathrm{I}\mathrm{know}.\mathrm{I}\mathrm{am}\mathrm{open}\mathrm{for}\mathrm{any}\mathrm{critics}\mathrm{if}$$$$\mathrm{I}\mathrm{made}\mathrm{any}\mathrm{mistakes}$$

Commented by Kunal12588 last updated on 12/Mar/19

$$thankyouverymuchsirs.$$

Commented by prakash jain last updated on 12/Mar/19

please visit the below link for definition of complex infinity http://mathworld.wolfram.com/ComplexInfinity.html

Terms of Service

Privacy Policy

Contact: info@tinkutara.com