Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 56301 by naka3546 last updated on 13/Mar/19

$$Minimumvalueofbthatsatisfythe$$ $$followinginequality$$ $$\frac{53}{201}<\frac{a}{b}<\frac{4}{15}is...$$

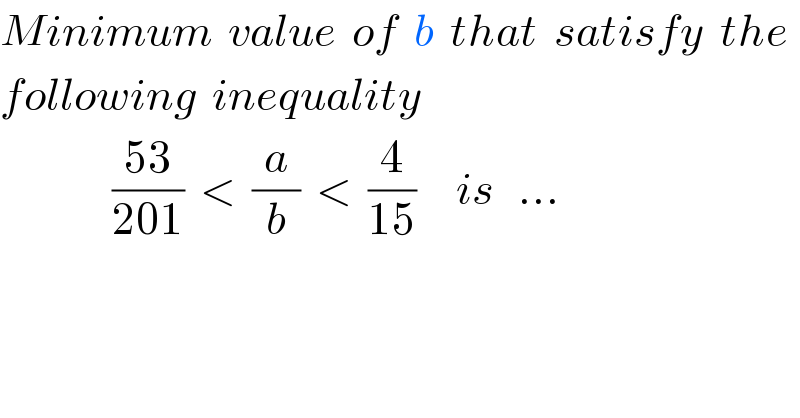
Commented bynaka3546 last updated on 13/Mar/19

$$a,barepositiveintegers.$$

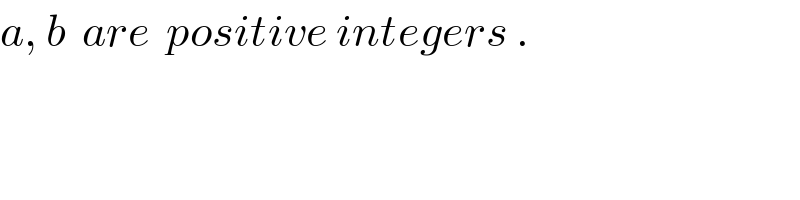
Answered by tanmay.chaudhury50@gmail.com last updated on 13/Mar/19

$$201=3\times 6715=3\times 5$$ $$\frac{53}{201}=\frac{265}{1005}and\frac{4}{15}=\frac{4\times 67}{15\times 67}=\frac{268}{1005}$$ $$\frac{a}{b}=\frac{266}{1005}\leftarrow firstanswer$$ $$\frac{a}{b}=\frac{267}{1005}\leftarrow secondanswer$$ $$\mathit{s}\mathit{o}\mathit{b}=1005$$

Commented bymr W last updated on 14/Mar/19

$$withmininmumb:\frac{9}{34}$$ $$thenextare\frac{13}{49},\frac{14}{53},\frac{17}{64},\frac{19}{72}....$$

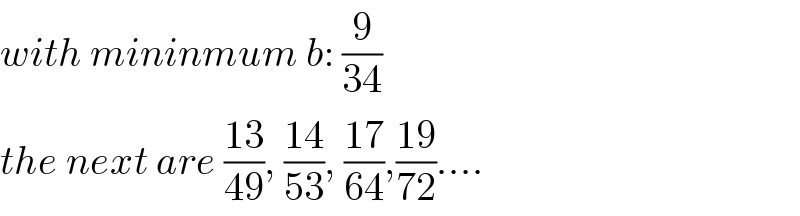
Commented bynaka3546 last updated on 14/Mar/19

$$howtogetit,sir.$$

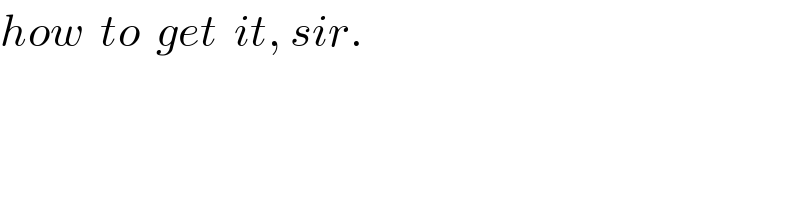
Commented byMJS last updated on 14/Mar/19

$$\frac{53}{201}<\frac{a}{b}<\frac{4}{15}$$ $$\frac{53}{201}b<a<\frac{4}{15}b$$ $$b\ne 15n\wedge b\ne 201n$$ $$\lceil \frac{53}{201}b\rceil >\lfloor \frac{4}{15}b\rfloor \mathrm{xor}\lceil \frac{53}{201}b\rceil =\lfloor \frac{4}{15}b\rfloor =a$$ $$\mathrm{now}\mathrm{we}\mathrm{must}\mathrm{try}$$

Commented byKunal12588 last updated on 13/Mar/19

$$sir\frac{53}{201}<\frac{33}{125}<\frac{4}{15}$$ $${don}^{\prime }tknowtherecanbesmalleranswers.$$

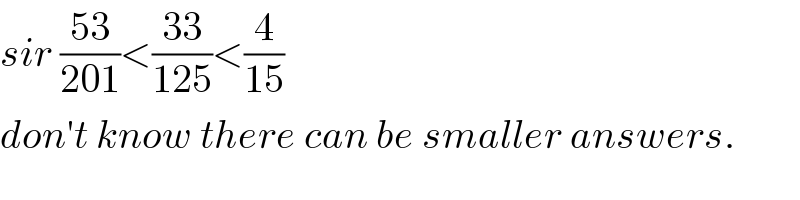
Commented bynaka3546 last updated on 14/Mar/19

$$\frac{9}{34}maybe,I{don}^{\prime }tknowaboutit.$$

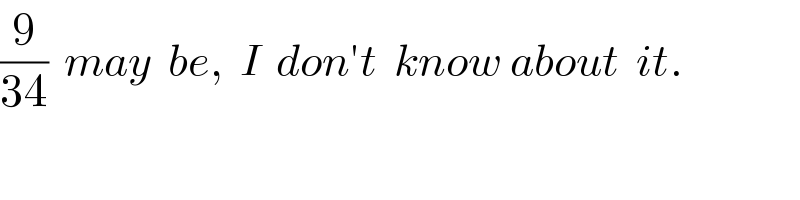
Answered by mr W last updated on 15/Mar/19

$$thisismymethod:$$ $$\frac{53}{201}<\frac{a}{b}<\frac{4}{15}$$ $$\Rightarrow \frac{201}{53}>\frac{b}{a}>\frac{15}{4}$$ $$\Rightarrow \frac{15a}{4}<b<\frac{201a}{53}$$ $$\Rightarrow \lfloor \frac{15a}{4}\rfloor +1⩽b⩽\lceil \frac{201a}{53}\rceil -1$$ $$$$ $$foragivenvalueofawecalculate$$ $$\lfloor \frac{15a}{4}\rfloor +1and\lceil \frac{201a}{53}\rceil -1.$$ $$if\lfloor \frac{15a}{4}\rfloor +1⩽\lceil \frac{201a}{53}\rceil -1,thenbexists,$$ $$andb=\lfloor \frac{15a}{4}\rfloor +1...\lceil \frac{201a}{53}\rceil -1.$$ $$$$ $$ifwestartwitha=1,2,3,...{we}^{\prime }llgetall$$ $$possible\left(infinite\right)solutions:$$ $$a=9\Rightarrow b=34$$ $$a=13\Rightarrow b=49$$ $$a=14\Rightarrow b=53$$ $$a=17\Rightarrow b=64$$ $$a=19\Rightarrow b=72$$ $$a=21\Rightarrow b=79$$ $$a=22\Rightarrow b=83$$ $$a=23\Rightarrow b=87$$ $$a=24\Rightarrow b=91$$ $$a=25\Rightarrow b=94$$ $$a=29\Rightarrow b=109$$ $$a=30\Rightarrow b=113$$ $$a=31\Rightarrow b=117$$ $$a=32\Rightarrow b=121$$ $$a=33\Rightarrow b=124,125$$ $$a=35\Rightarrow b=132$$ $$......$$ $$a=117\Rightarrow b=439,440,442,443$$ $$......$$

Commented bymr W last updated on 15/Mar/19

$$isthereaneasierwaythanthis?$$

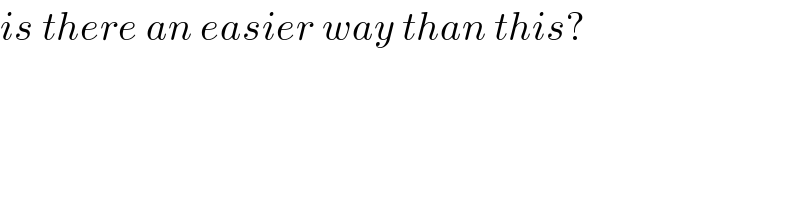
Commented byMJS last updated on 16/Mar/19

$$\mathrm{no}.$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com