
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 56330 by maxmathsup by imad last updated on 14/Mar/19
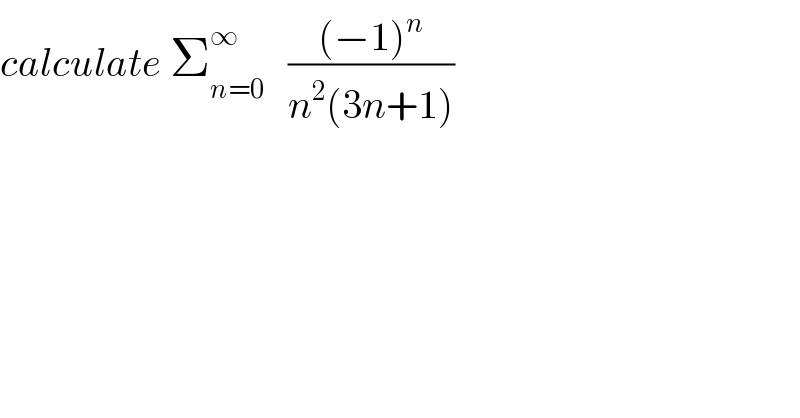
Commented by maxmathsup by imad last updated on 24/Mar/19
![let decompose F(x)=(1/(x^2 (3x+1))) ⇒F(x)=(a/x) +(b/x^2 ) +(c/(3x+1)) b=lim_(x→0) x^2 F(x)=1 c =lim_(x→−(1/3)) (3x+1)F(x) =9 ⇒F(x)=(a/x) +(1/x^2 ) +(9/(3x+1)) F(−1) =−(1/2) =−a +1 −(9/2) ⇒−1 =−2a +2 −9 ⇒−1=−2a−7 ⇒ 2a =−6 ⇒a =−3 ⇒F(x)=−(3/x) +(1/x^2 ) +(9/(3x+1)) ⇒ Σ_(n=1) ^∞ (((−1)^n )/(n^2 (3n+1))) =−3 Σ_(n=1) ^∞ (((−1)^n )/n) +Σ_(n=1) ^∞ (((−1)^n )/n^2 ) +9 Σ_(n=1) ^∞ (((−1)^n )/(3n+1)) but Σ_(n=1) ^∞ (((−1)^n )/n) =−ln(2) let find Σ_(n=1) ^∞ (((−1)^n )/n^2 ) we have Σ_(n=1) ^∞ (((−1)^n )/n^2 ) =Σ_(n=1) ^∞ (1/(4n^2 )) −Σ_(n=0) ^∞ (1/((2n+1)^2 )) Σ_(n=1) ^∞ (1/n^2 ) =Σ_(n=1) ^∞ (1/(4n^2 )) +Σ_(n=0) ^∞ (1/((2n+1)^2 )) ⇒Σ_(n=0) ^∞ (1/((2n+1)^2 )) =(3/4) (π^2 /6) =(π^2 /8) ⇒ Σ_(n=1) ^∞ (((−1)^n )/n^2 ) =(π^2 /(24)) −(π^2 /8) =((π^2 −3π^2 )/(24)) =−(π^2 /(12)) let determine Σ_(n=1) ^∞ (((−1)^n )/(3n+1)) let S(x) =Σ_(n=1) ^∞ (−1)^n (x^(3n+1) /(3n+1)) with ∣x∣<1 ⇒(dS/dx)(x) =Σ_(n=1) ^∞ (−1)^n x^(3n) =Σ_(n=1) ^∞ (−x^3 )^n =(1/(1+x^3 )) −1 =((−x^3 )/(1+x^3 )) ⇒S(x) =∫_0 ^x ((−t^3 )/(1+t^3 )) dt +λ S(0)=0 ⇒λ =0 ⇒ S(x) =−∫_0 ^x ((t^3 +1−1)/(t^3 +1)) dt =−x + ∫_0 ^x (dt/(t^3 +1)) let decompose F(t) =(1/(t^3 +1)) =(1/((t+1)(t^2 −t+1))) F(t)=(a/(t+1)) +((bt +c)/(t^2 −t +1)) a =lim_(t→−1) (t+1)F(t)=(1/3) lim_(t→+∞) t F(t) =0 =a+b ⇒b =−(1/3) ⇒F(t) =(1/(3(t+1))) −(1/3) ((t−3c)/(t^2 −t +1)) F(o) =1 =(1/3) +c ⇒c =(2/3) ⇒F(t)=(1/(3(t+1))) −(1/3) ((t−2)/(t^2 −t+1)) ⇒ ∫ F(t)dt =(1/3)ln∣t+1∣ −(1/6) ∫ ((2t−1−3)/(t^2 −t+1)) dt =(1/3)ln∣t+1∣−(1/6)ln(t^2 −t +1) +(1/2) ∫ (dt/(t^2 −t +1)) but ∫ (dt/(t^2 −t +1)) =∫ (dt/((t−(1/2))^2 +(3/4))) =_(t+(1/2)=((√3)/2)u) ∫ (1/((3/4)(1+u^2 ))) ((√3)/2) du =(4/3) ((√3)/2) arctanu +c =(2/(√3)) arctan(((2t+1)/(√3))) ⇒ S(x)=−x +[(1/3)ln∣t+1∣−(1/6)ln(t^2 −t+1)+(1/(√3)) arctan(((2t+1)/(√3)))]_0 ^x =−x +{(1/3)ln∣x+1∣−(1/6)ln(x^2 −x+1)+(1/(√3)) arctan(((2x+1)/(√3)))−(1/(√3)) arctan((1/(√3)))} ⇒ Σ_(n=1) ^∞ (((−1)^n )/(3n+1)) =S(1) =−1 +(1/3)ln(2) +(1/(√3)) arctan((√3))−(1/(√3)) arctan((1/(√3))) =−1 +(1/3)ln(2) +(1/(√3)) arctan((√3))−(1/(√3))((π/2) −arctan((√3))) =−1 +((ln(2))/3) +(2/(√3)) arctan((√3)) −(π/(2(√3))) ⇒ Σ_(n=1) ^∞ (((−1)^n )/(n^2 (3n+1))) = 3ln(2) −(π^2 /(12)) −9 +3ln(2) +((18)/(√3)) arctan((√3)) −((9π)/(2(√3))) .](Q56814.png)
| ||
Question and Answers Forum | ||
Previous in Relation and Functions Next in Relation and Functions | ||
Question Number 56330 by maxmathsup by imad last updated on 14/Mar/19 | ||
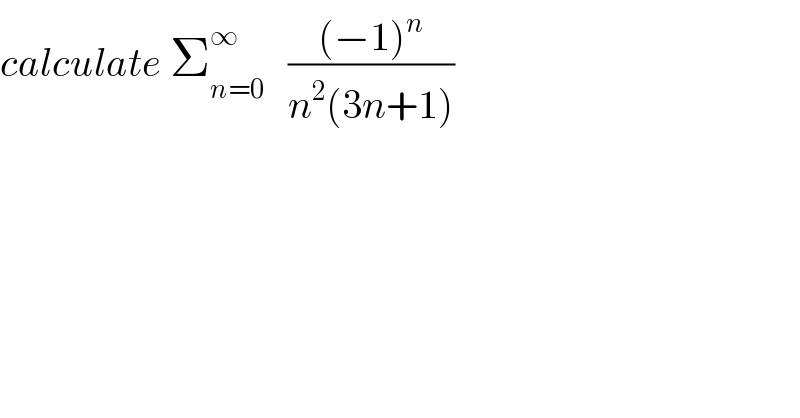 | ||
Commented by maxmathsup by imad last updated on 24/Mar/19 | ||
![let decompose F(x)=(1/(x^2 (3x+1))) ⇒F(x)=(a/x) +(b/x^2 ) +(c/(3x+1)) b=lim_(x→0) x^2 F(x)=1 c =lim_(x→−(1/3)) (3x+1)F(x) =9 ⇒F(x)=(a/x) +(1/x^2 ) +(9/(3x+1)) F(−1) =−(1/2) =−a +1 −(9/2) ⇒−1 =−2a +2 −9 ⇒−1=−2a−7 ⇒ 2a =−6 ⇒a =−3 ⇒F(x)=−(3/x) +(1/x^2 ) +(9/(3x+1)) ⇒ Σ_(n=1) ^∞ (((−1)^n )/(n^2 (3n+1))) =−3 Σ_(n=1) ^∞ (((−1)^n )/n) +Σ_(n=1) ^∞ (((−1)^n )/n^2 ) +9 Σ_(n=1) ^∞ (((−1)^n )/(3n+1)) but Σ_(n=1) ^∞ (((−1)^n )/n) =−ln(2) let find Σ_(n=1) ^∞ (((−1)^n )/n^2 ) we have Σ_(n=1) ^∞ (((−1)^n )/n^2 ) =Σ_(n=1) ^∞ (1/(4n^2 )) −Σ_(n=0) ^∞ (1/((2n+1)^2 )) Σ_(n=1) ^∞ (1/n^2 ) =Σ_(n=1) ^∞ (1/(4n^2 )) +Σ_(n=0) ^∞ (1/((2n+1)^2 )) ⇒Σ_(n=0) ^∞ (1/((2n+1)^2 )) =(3/4) (π^2 /6) =(π^2 /8) ⇒ Σ_(n=1) ^∞ (((−1)^n )/n^2 ) =(π^2 /(24)) −(π^2 /8) =((π^2 −3π^2 )/(24)) =−(π^2 /(12)) let determine Σ_(n=1) ^∞ (((−1)^n )/(3n+1)) let S(x) =Σ_(n=1) ^∞ (−1)^n (x^(3n+1) /(3n+1)) with ∣x∣<1 ⇒(dS/dx)(x) =Σ_(n=1) ^∞ (−1)^n x^(3n) =Σ_(n=1) ^∞ (−x^3 )^n =(1/(1+x^3 )) −1 =((−x^3 )/(1+x^3 )) ⇒S(x) =∫_0 ^x ((−t^3 )/(1+t^3 )) dt +λ S(0)=0 ⇒λ =0 ⇒ S(x) =−∫_0 ^x ((t^3 +1−1)/(t^3 +1)) dt =−x + ∫_0 ^x (dt/(t^3 +1)) let decompose F(t) =(1/(t^3 +1)) =(1/((t+1)(t^2 −t+1))) F(t)=(a/(t+1)) +((bt +c)/(t^2 −t +1)) a =lim_(t→−1) (t+1)F(t)=(1/3) lim_(t→+∞) t F(t) =0 =a+b ⇒b =−(1/3) ⇒F(t) =(1/(3(t+1))) −(1/3) ((t−3c)/(t^2 −t +1)) F(o) =1 =(1/3) +c ⇒c =(2/3) ⇒F(t)=(1/(3(t+1))) −(1/3) ((t−2)/(t^2 −t+1)) ⇒ ∫ F(t)dt =(1/3)ln∣t+1∣ −(1/6) ∫ ((2t−1−3)/(t^2 −t+1)) dt =(1/3)ln∣t+1∣−(1/6)ln(t^2 −t +1) +(1/2) ∫ (dt/(t^2 −t +1)) but ∫ (dt/(t^2 −t +1)) =∫ (dt/((t−(1/2))^2 +(3/4))) =_(t+(1/2)=((√3)/2)u) ∫ (1/((3/4)(1+u^2 ))) ((√3)/2) du =(4/3) ((√3)/2) arctanu +c =(2/(√3)) arctan(((2t+1)/(√3))) ⇒ S(x)=−x +[(1/3)ln∣t+1∣−(1/6)ln(t^2 −t+1)+(1/(√3)) arctan(((2t+1)/(√3)))]_0 ^x =−x +{(1/3)ln∣x+1∣−(1/6)ln(x^2 −x+1)+(1/(√3)) arctan(((2x+1)/(√3)))−(1/(√3)) arctan((1/(√3)))} ⇒ Σ_(n=1) ^∞ (((−1)^n )/(3n+1)) =S(1) =−1 +(1/3)ln(2) +(1/(√3)) arctan((√3))−(1/(√3)) arctan((1/(√3))) =−1 +(1/3)ln(2) +(1/(√3)) arctan((√3))−(1/(√3))((π/2) −arctan((√3))) =−1 +((ln(2))/3) +(2/(√3)) arctan((√3)) −(π/(2(√3))) ⇒ Σ_(n=1) ^∞ (((−1)^n )/(n^2 (3n+1))) = 3ln(2) −(π^2 /(12)) −9 +3ln(2) +((18)/(√3)) arctan((√3)) −((9π)/(2(√3))) .](Q56814.png) | ||