Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 56383 by Tawa1 last updated on 15/Mar/19

Commented by Tawa1 last updated on 16/Mar/19

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by maxmathsup by imad last updated on 15/Mar/19

∫_(−1) ^7 (dx/((^3 (√(x+1)))))dx =_(x+1 =t^3 ) ∫_0 ^(2(√2)) ((3t^2 dt)/t) =3 ∫_0 ^(2(√2)) tdt =3[(t^2 /2)]_0 ^(2(√2)) =(3/2){2(√2))^2 =12.

$$\int_{−\mathrm{1}} ^{\mathrm{7}} \:\:\frac{{dx}}{\left(^{\mathrm{3}} \sqrt{{x}+\mathrm{1}}\right)}{dx}\:=_{{x}+\mathrm{1}\:={t}^{\mathrm{3}} } \:\:\:\int_{\mathrm{0}} ^{\mathrm{2}\sqrt{\mathrm{2}}} \:\:\:\frac{\mathrm{3}{t}^{\mathrm{2}} {dt}}{{t}}\:=\mathrm{3}\:\int_{\mathrm{0}} ^{\mathrm{2}\sqrt{\mathrm{2}}} {tdt}\:=\mathrm{3}\left[\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}\left\{\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \:=\mathrm{12}. \\ $$

Commented by maxmathsup by imad last updated on 16/Mar/19

we can use the result ∫_0 ^∞ (t^(a−1) /(1+t))dt =(π/(sin(πa))) with 0<a<1 so changement x =t^(1/4) give ∫_0 ^∞ (dx/(1+x^4 )) =∫_0 ^∞ (1/(4(1+t))) t^((1/4)−1) dt =(1/4) (π/(sin((π/4)))) =(π/(4 ((√2)/2))) =(π/(2(√2))) .

$${we}\:{can}\:{use}\:{the}\:{result}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{{a}−\mathrm{1}} }{\mathrm{1}+{t}}{dt}\:=\frac{\pi}{{sin}\left(\pi{a}\right)}\:\:{with}\:\mathrm{0}<{a}<\mathrm{1}\:{so} \\ $$$${changement}\:{x}\:={t}^{\frac{\mathrm{1}}{\mathrm{4}}} \:\:{give}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{4}} }\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{1}+{t}\right)}\:{t}^{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} {dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\:\frac{\pi}{{sin}\left(\frac{\pi}{\mathrm{4}}\right)}\:=\frac{\pi}{\mathrm{4}\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}\:=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}\:. \\ $$

Commented by Abdo msup. last updated on 16/Mar/19

thank you so much sir.

$${thank}\:{you}\:{so}\:{much}\:{sir}. \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 15/Mar/19

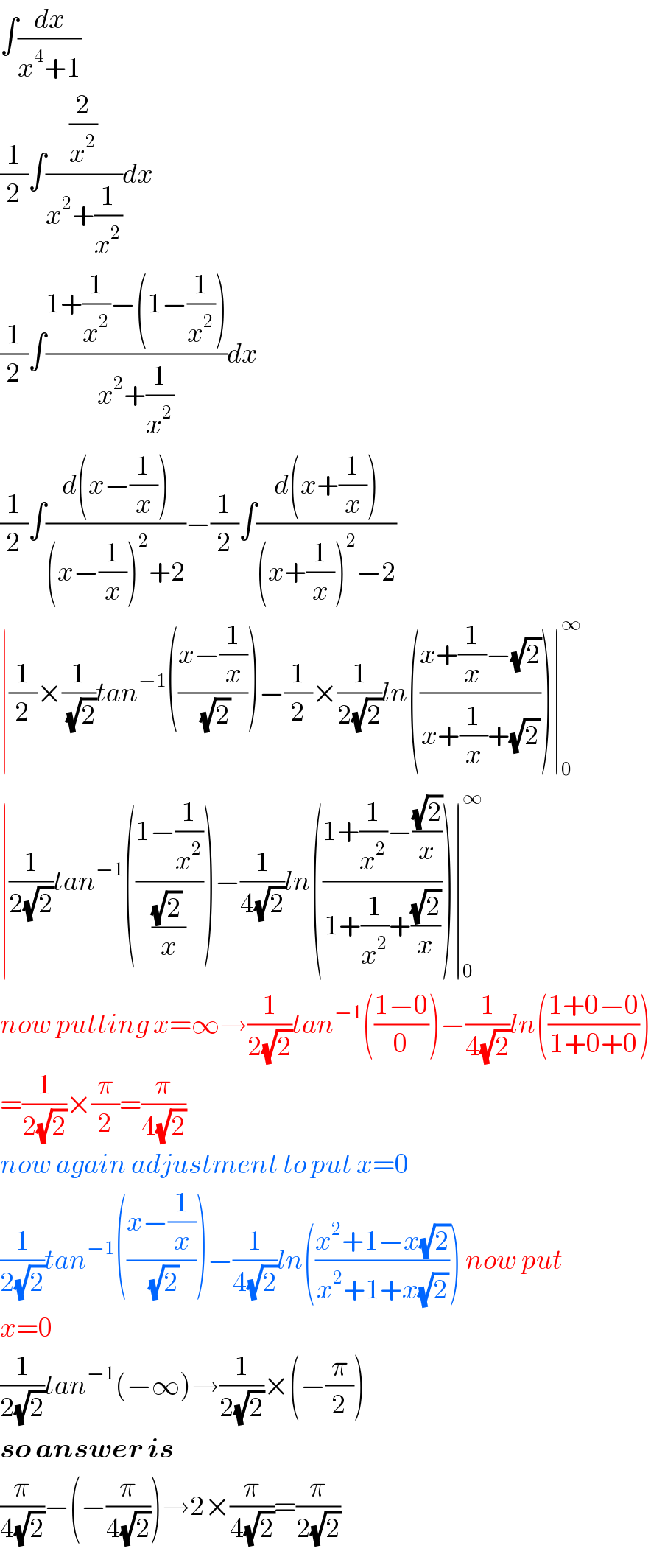
∫(dx/(x^4 +1)) (1/2)∫((2/x^2 )/(x^2 +(1/x^2 )))dx (1/2)∫((1+(1/x^2 )−(1−(1/x^2 )))/(x^2 +(1/x^2 )))dx (1/2)∫((d(x−(1/x)))/((x−(1/x))^2 +2))−(1/2)∫((d(x+(1/x)))/((x+(1/x))^2 −2)) ∣(1/2)×(1/(√2))tan^(−1) (((x−(1/x))/(√2)))−(1/2)×(1/(2(√2)))ln(((x+(1/x)−(√2))/(x+(1/x)+(√2))))∣_0 ^∞ ∣(1/(2(√2)))tan^(−1) (((1−(1/x^2 ))/(((√2) )/x)))−(1/(4(√2)))ln(((1+(1/x^2 )−((√2)/x))/(1+(1/x^2 )+((√2)/x))))∣_0 ^∞ now putting x=∞→(1/(2(√2)))tan^(−1) (((1−0)/0))−(1/(4(√2)))ln(((1+0−0)/(1+0+0))) =(1/(2(√2)))×(π/2)=(π/(4(√2))) now again adjustment to put x=0 (1/(2(√2)))tan^(−1) (((x−(1/x))/(√2)))−(1/(4(√2)))ln(((x^2 +1−x(√2))/(x^2 +1+x(√2)))) now put x=0 (1/(2(√2)))tan^(−1) (−∞)→(1/(2(√2)))×(−(π/2)) so answer is (π/(4(√2)))−(−(π/(4(√2))))→2×(π/(4(√2)))=(π/(2(√2)))

$$\int\frac{{dx}}{{x}^{\mathrm{4}} +\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\frac{\mathrm{2}}{{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)}{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({x}−\frac{\mathrm{1}}{{x}}\right)}{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({x}+\frac{\mathrm{1}}{{x}}\right)}{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{2}} \\ $$$$\mid\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(\frac{{x}−\frac{\mathrm{1}}{{x}}}{\sqrt{\mathrm{2}}}\right)−\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{ln}\left(\frac{{x}+\frac{\mathrm{1}}{{x}}−\sqrt{\mathrm{2}}}{{x}+\frac{\mathrm{1}}{{x}}+\sqrt{\mathrm{2}}}\right)\mid_{\mathrm{0}} ^{\infty} \\ $$$$\mid\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\frac{\sqrt{\mathrm{2}}\:}{{x}}}\right)−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}{ln}\left(\frac{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\frac{\sqrt{\mathrm{2}}}{{x}}}{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\frac{\sqrt{\mathrm{2}}}{{x}}}\right)\mid_{\mathrm{0}} ^{\infty} \\ $$$${now}\:{putting}\:{x}=\infty\rightarrow\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}−\mathrm{0}}{\mathrm{0}}\right)−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}{ln}\left(\frac{\mathrm{1}+\mathrm{0}−\mathrm{0}}{\mathrm{1}+\mathrm{0}+\mathrm{0}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}×\frac{\pi}{\mathrm{2}}=\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}} \\ $$$${now}\:{again}\:{adjustment}\:{to}\:{put}\:{x}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(\frac{{x}−\frac{\mathrm{1}}{{x}}}{\sqrt{\mathrm{2}}}\right)−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}{ln}\left(\frac{{x}^{\mathrm{2}} +\mathrm{1}−{x}\sqrt{\mathrm{2}}}{{x}^{\mathrm{2}} +\mathrm{1}+{x}\sqrt{\mathrm{2}}}\right)\:{now}\:{put} \\ $$$${x}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(−\infty\right)\rightarrow\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}×\left(−\frac{\pi}{\mathrm{2}}\right) \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{answer}}\:\boldsymbol{{is}} \\ $$$$\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}−\left(−\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}\right)\rightarrow\mathrm{2}×\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$

Commented by Tawa1 last updated on 15/Mar/19

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 15/Mar/19

lim_(a→−1) ∫_a ^7 (dx/((1+x)^(1/3) )) lim_(a→−1) ∣(((1+x)^(((−1)/3)+1) )/(2/3))∣_a ^7 =lim_(a→−1) [(3/2)(8)^(2/3) −(3/2)(1+a)^(2/3) ] =(3/2)×4→6 ans

$$\underset{{a}\rightarrow−\mathrm{1}} {\mathrm{lim}}\int_{{a}} ^{\mathrm{7}} \frac{{dx}}{\left(\mathrm{1}+{x}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} } \\ $$$$\underset{{a}\rightarrow−\mathrm{1}} {\mathrm{lim}}\mid\frac{\left(\mathrm{1}+{x}\right)^{\frac{−\mathrm{1}}{\mathrm{3}}+\mathrm{1}} }{\frac{\mathrm{2}}{\mathrm{3}}}\mid_{{a}} ^{\mathrm{7}} \\ $$$$=\underset{{a}\rightarrow−\mathrm{1}} {\mathrm{lim}}\left[\frac{\mathrm{3}}{\mathrm{2}}\left(\mathrm{8}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} −\frac{\mathrm{3}}{\mathrm{2}}\left(\mathrm{1}+{a}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \right] \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}×\mathrm{4}\rightarrow\mathrm{6}\:{ans} \\ $$

Commented by Tawa1 last updated on 15/Mar/19

God bless you sir.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com