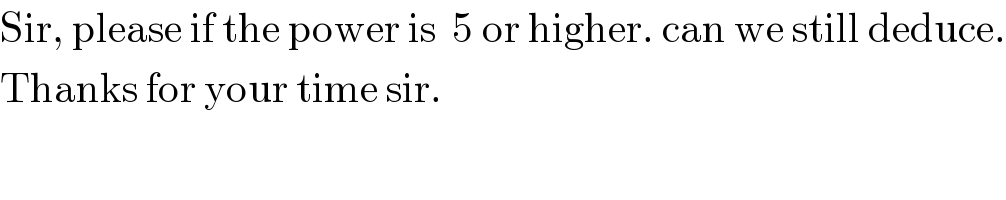Please is there any way to reduce a polynomial of 4th degree and solve. Or probably a polynomial of nth power to smaller power.


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 56479 by Tawa1 last updated on 17/Mar/19

$Please is there any way to reduce a polynomial of 4 th degree$ $and solve . Or probably a polynomial of nth power to smaller$ $power .$
	Answered by ajfour last updated on 17/Mar/19

	$x^{4} + {a x}^{3} + {b x}^{2} + c x + d = 0$ $l e t x = t - \frac{a}{4}$ $t^{4} - {a t}^{3} + \frac{3}{8} a^{2} t^{2} - \frac{a^{3}}{16} t + \frac{a^{4}}{256}$ $+ {a t}^{3} - \frac{3 a^{2}}{4} t^{2} + \frac{3 a^{3}}{16} t - \frac{a^{4}}{64}$ $+ {b t}^{2} - \frac{a b}{2} t + \frac{a^{2} b}{16} + c t - \frac{a c}{4} + d = 0$ $\Rightarrow t^{4} + (b - \frac{3 a^{2}}{8}) t^{2} + (\frac{a^{3}}{8} - \frac{a b}{2} + c) t$ $+ (\frac{3 a^{4}}{256} + \frac{a^{2} b}{16} - \frac{a c}{4} + d) = 0$ $S a y w e h a v e n o w$ $t^{4} + {B t}^{2} + C t + D$ $= (t^{2} + p t + q) (t^{2} - p t + r) = 0$ $\Rightarrow t^{4} + (r - p^{2} + q) t^{2} + p (r - q) t + q r = 0$ $\Rightarrow q + r = B + p^{2}$ $r - q = C / p$ $q r = D$ $\Rightarrow 2 r = (B + p^{2}) + \frac{C}{p} . . . (i)$ $2 q = (B + p^{2}) - \frac{C}{p} . . . (i i)$ $\Rightarrow {(B + p^{2})}^{2} - \frac{C^{2}}{p^{2}} = 4 D$ $l e t p^{2} = z$ $\Rightarrow z {(B + z)}^{2} - 4 D z - C^{2} = 0$ $\Rightarrow z^{3} + 2 {B z}^{2} + (B^{2} - 4 D) z - C^{2} = 0$ $F i n d z = p^{2} f r o m a b o v e e q .$ $T h e n u s i n g (i) & (i i) o b t a i n$ $q a n d r .$ $N o w w e h a v e$ $(t^{2} + p t + q) (t^{2} - p t + r) = 0$ $\Rightarrow t = - \frac{p}{2} \pm \sqrt{\frac{p^{2}}{4} - q} o r$ $t = \frac{p}{2} \pm \sqrt{\frac{p^{2}}{4} - r}$ $& x = t - \frac{a}{4} .$
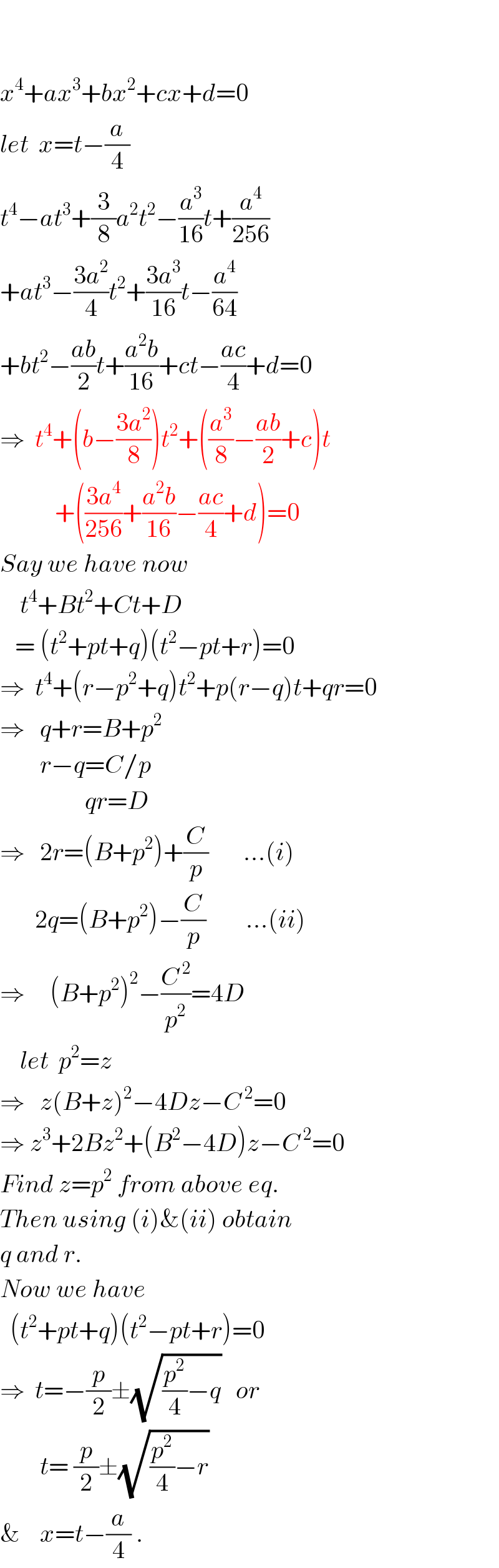
	Commented by Tawa1 last updated on 17/Mar/19

	$God bless you sir, i look forward for the success sir$
	Commented by ajfour last updated on 17/Mar/19

	$O r a f t e r$ $t^{4} + {B t}^{2} + C t + D = 0$ $w e l e t x = \frac{p t + q}{t + 1} t h e n$ ${(p t + q)}^{4} + B {(p t + q)}^{2} {(t + 1)}^{2} +$ $C (p t + q) {(t + 1)}^{3} + D {(t + 1)}^{4} = 0$ $\Rightarrow$ $p^{4} t^{4} + 4 p^{3} {q t}^{3} + 6 p^{2} q^{2} t^{2} + 4 {p q}^{3} t + q^{4}$ $+ B (p^{2} t^{2} + 2 p q t + q^{2}) (t^{2} + 2 t + 1) +$ $C (p t + q) (t^{3} + 3 t^{2} + 3 t + 1) +$ $D (t^{4} + 4 t^{3} + 6 t^{2} + 4 t + 1) = 0$ $\Rightarrow$ $__________________________$ $(p^{4} + {B p}^{2} + C p + D) t^{4} +$ $(4 p^{3} q + 2 {B p}^{2} + 2 B p q + 3 C p + C q + 4 D) t^{3}$ $+ (6 p^{2} q^{2} + {B p}^{2} + 4 B p q + {B q}^{2} + 3 C p + 3 C q + 6 D) t^{2}$ $+ (4 {p q}^{3} + 2 B p q + 2 {B q}^{2} + C p + 3 C q + 4 D) t$ $+ (q^{4} + {B q}^{2} + C q + D) = 0$ $__________________________$ $& i f w e l e t c o e f f i c i e n t s o f t^{3} & t$ $t o b e z e r o w e o b t a i n a q u a d r a t i c$ $i n t^{2} .$ $4 p^{3} q + 2 {B p}^{2} + 2 B p q + 3 C p + C q + 4 D = 0$ $4 {p q}^{3} + 2 B p q + 2 {B q}^{2} + C p + 3 C q + 4 D = 0$ $s u b t r a c t i n g w e g e t$ $4 p q (p + q) + 2 B (p + q) + 2 C = 0 . . (I)$ $A n d a d d i n g w e g e t$ $(4 p q + 2 B) (p^{2} + q^{2}) + 4 B p q +$ $4 C (p + q) + 8 D = 0 . . . (I I)$ $S o l v i n g t h i s p a i r$ $o f e q s . (I) & (I I),$ ${w e}^{'} d h a v e r e d u c e d a$ $b i q u a d r a t i c t o a q u a d r a t i c .$ $r e w r i t i n g e q . (I I)$ $(4 p q + 2 B) [{(p + q)}^{2} - 2 p q] + 4 B p q$ $+ 4 C (p + q) + 8 D = 0$ $\Rightarrow 4 C (p + q) + 8 D = - (4 p q + 2 B) {(p + q)}^{2}$ $u s i n g (I) h e r e i n$ $\Rightarrow 4 C (p + q) + 8 D = 2 (p + q) [C + B (p + q)]$ $\Rightarrow B {(p + q)}^{2} - C (p + q) - 4 D = 0$ $\Rightarrow p + q = \frac{C}{2} \pm \sqrt{\frac{C^{2}}{4} + 4 D} = k$ $p q = - \frac{B}{2} - \frac{C}{2 (p + q)}$ $= - \frac{B}{2} - \frac{C}{2 k} = l$ $p, q a r e r o o t s o f$ $z^{2} - k z + l = 0$ $p, q = \frac{k}{2} \pm \sqrt{\frac{k^{2}}{4} - l}$ $N o w w e h a v e$ $(p^{4} + {B p}^{2} + C p + D) t^{4}$ $+ (6 p^{2} q^{2} + {B p}^{2} + 4 B p q + {B q}^{2} + 3 C p + 3 C q + 6 D) t^{2}$ $+ (q^{4} + {B q}^{2} + C q + D) = 0$ $w h i c h i s a q u a d r a t i c i n t^{2},$ $a n d c a n b e s o l v e d .$ $A n d x = \frac{p t + q}{t + 1} . ◼$
	Commented by Tawa1 last updated on 17/Mar/19

	$Wow, God bless you sir . I appreciate . . .$
	Commented by Tawa1 last updated on 17/Mar/19

	$Sir, please if the power is 5 or higher . can we still deduce .$ $Thanks for your time sir .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum