
Question and Answers Forum
Question Number 56498 by kelly33 last updated on 17/Mar/19
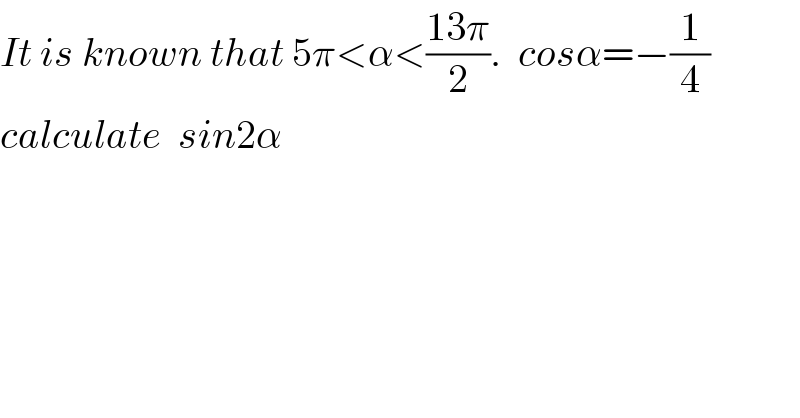
Commented bykelly33 last updated on 17/Mar/19

Answered by tanmay.chaudhury50@gmail.com last updated on 17/Mar/19

Commented byMJS last updated on 17/Mar/19
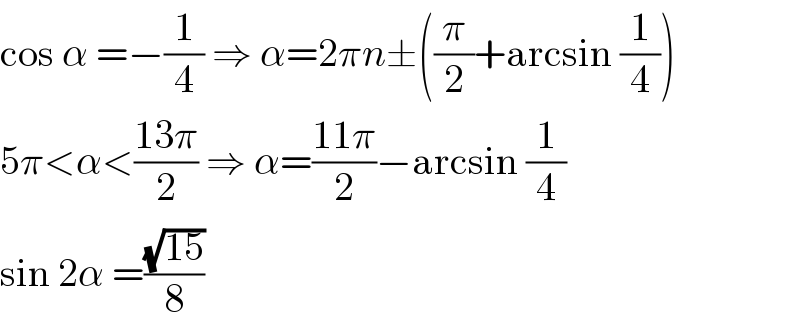
Commented bykelly33 last updated on 18/Mar/19
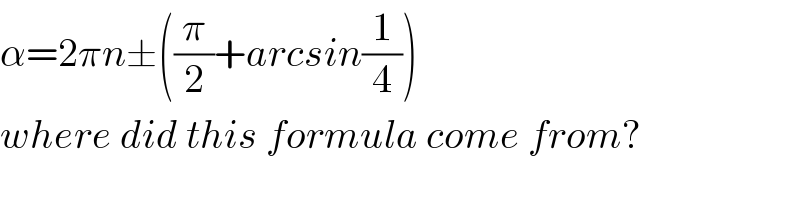
Commented byMJS last updated on 19/Mar/19
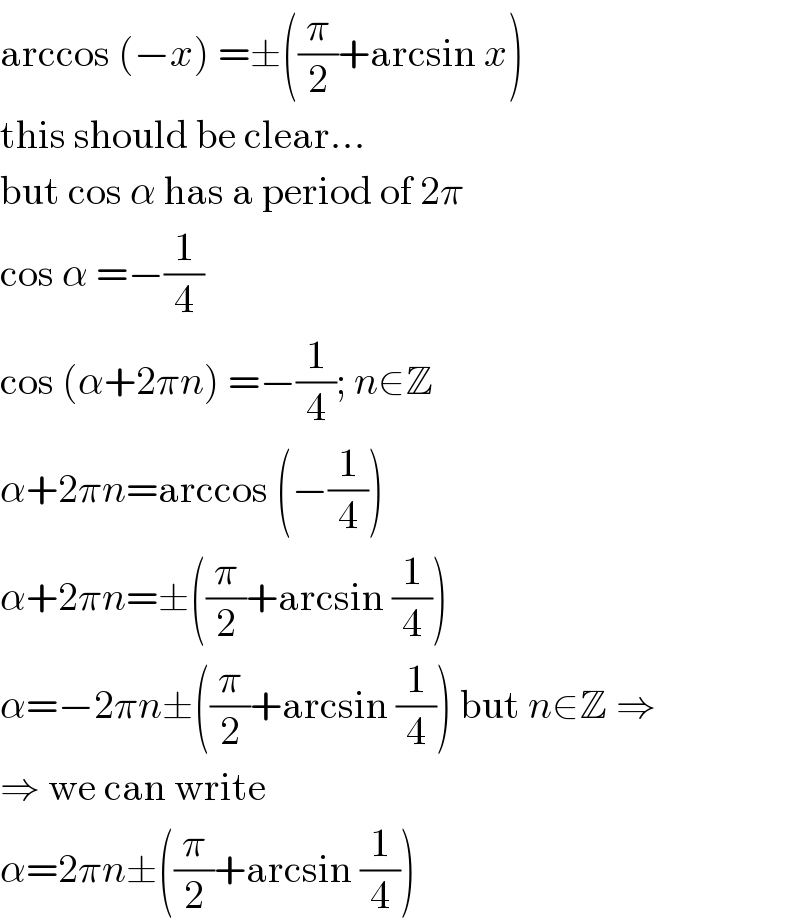
Commented bykelly33 last updated on 19/Mar/19

Commented bykelly33 last updated on 19/Mar/19
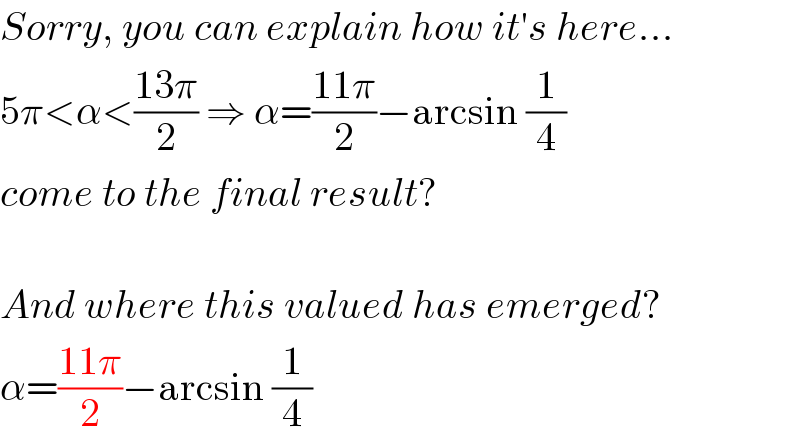
Commented bykelly33 last updated on 19/Mar/19
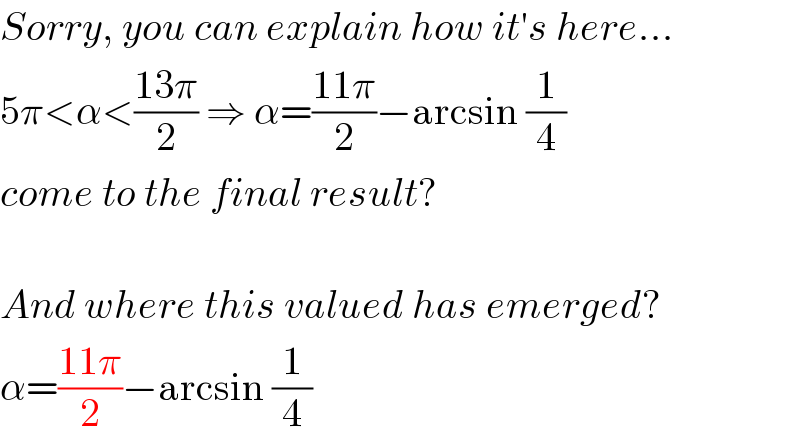
Commented byMJS last updated on 19/Mar/19
![general result: α=2πn±((π/2)+arcsin (1/4)) now we must test which n∈Z makes α fit into the interval. α_n ^− =2πn−((π/2)+arcsin (1/4)) α_n ^+ =2πn+((π/2)+arcsin (1/4)) ]5π;((13)/2)π[ ≈ ]15.708; 20.420[ α_3 ^− ≈17.026 is the only one to fit ⇒ α=6π−((π/2)+arcsin (1/4))=((11π)/2)−arcsin (1/4) sin 2α =sin (11π−2arcsin (1/4)) = [because of period 2π: sin (11π−θ) =sin θ] =sin (2arcsin (1/4)) = [sin 2θ =2sin θ cos θ] =2(sin arcsin (1/4))(cos arcsin (1/4))= =2×(1/4)×cos arcsin (1/4) = [cos arcsin t =sin arcsin t =(√(1−t^2 ))] =(1/2)(√(1−(1/(16))))=((√(15))/8)](Q56609.png)
