
Question and Answers Forum
Previous in Differential Equation Next in Differential Equation
Question Number 56580 by subhankar10 last updated on 18/Mar/19
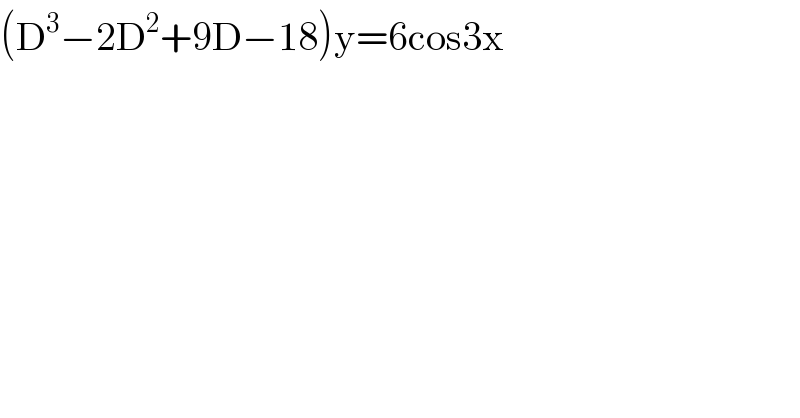
Answered by tanmay.chaudhury50@gmail.com last updated on 19/Mar/19
![let y=e^(mx) be a solution Dy=me^(mx) D^2 y=m^2 e^(mx) .. so complimentary function m^3 e^(mx) −2m^2 e^(mx) +9me^(mx) −18e^(mx) =0 e^(mx) (m^3 −2m^2 +9m−18)=0 e^(mx) ≠0 m^3 −2m^2 +9m−18=0 m^2 (n−2)+9(m−2)=0 (m−2)(m^2 +9)=0 m=2 and ±3i C.F C_1 e^(2x) +C_2 e^(i3x) +C_3 e^(−i3x) Particular intregal y=((6cos3x)/(D^3 −2D^2 +9D−18)) =6×((cos3x)/(D^2 (D−2)+9(D−2))) =6×((cos3x)/((D−2)(D^2 +9))) =6×(((D+2) cos3x)/((D^2 −4)(D^2 +9))) =(6/((−3^2 −4)))×((−3sin3x+2cos3x)/(D^2 +9)) =((−6)/(13))×((−3sin3x+2cos3x)/(D^2 +9)) =(6/(13))×(((3sin3x−2cos3x))/(D^2 +9)) =(6/(13))×((rsin(3x−θ))/(D^2 +9)) [r=(√(3^2 +2^2 )) =(√(13)) tanθ=(2/3)] p=(6/((√(13)) ))×((cos(3x−θ))/(D^2 +9)) q=(6/(√(13)))×((sin(3x−θ))/(D^2 +9)) p+iq=(6/(√(13)))×(e^(i(3x−θ)) /(D^2 +9)) p+iq=(6/(√(13)))×e^(−iθ) ×(e^(i×3x) /(D^2 +9)) p+iq=(6/(√(13)))×e^(−iθ) ×(e^(i3x) /((D+i3)(D−i3))) p+iq=(6/(√(13)))×(cosθ−isinθ)×(e^(i3x) /((i3+i3)(D+i3−i3)))×1 =(6/(√(13)))×((3/(√(13)))−i×(2/(√(13))))×(((cos3x+isin3x))/(6i))×x =(1/(13))×((3i+2)/i^2 )×(xcos3x+ixsin3x) =((−1)/(13))(i3xcos3x−3xsin3x+2xcos3x+i2xsin3x) =((−1)/(13)){(2xcos3x−3xsin3x)+i(3xcos3x+2xsin3x)} =((−x)/(13))(2cos3x−3sin3x)+((−ix)/(13))(3cos3x+2sin3x) now our answer is related to complex part so answer is Particular intregal is =((−x)/(13))(3cos3x+2sin3x) so complte answer is=C.F+P.I y=C_1 e^(2x) +C_2 e^(i3x) +C_3 e^(−i3x) +((−x)/(13))(3cos3x+2sin3x)](Q56581.png)
| ||
Question and Answers Forum | ||
Previous in Differential Equation Next in Differential Equation | ||
Question Number 56580 by subhankar10 last updated on 18/Mar/19 | ||
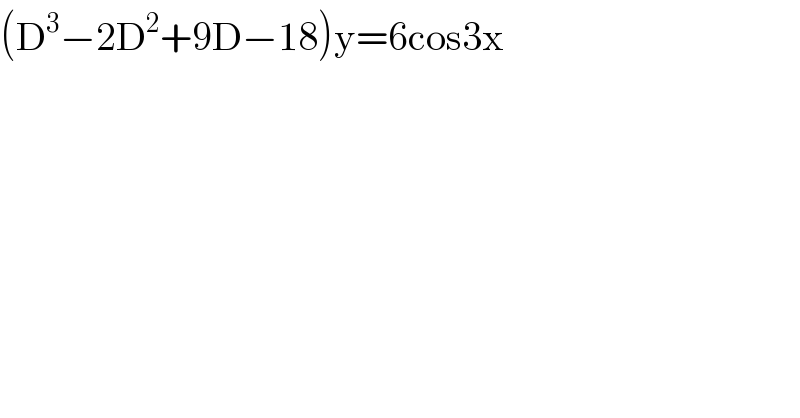 | ||
Answered by tanmay.chaudhury50@gmail.com last updated on 19/Mar/19 | ||
![let y=e^(mx) be a solution Dy=me^(mx) D^2 y=m^2 e^(mx) .. so complimentary function m^3 e^(mx) −2m^2 e^(mx) +9me^(mx) −18e^(mx) =0 e^(mx) (m^3 −2m^2 +9m−18)=0 e^(mx) ≠0 m^3 −2m^2 +9m−18=0 m^2 (n−2)+9(m−2)=0 (m−2)(m^2 +9)=0 m=2 and ±3i C.F C_1 e^(2x) +C_2 e^(i3x) +C_3 e^(−i3x) Particular intregal y=((6cos3x)/(D^3 −2D^2 +9D−18)) =6×((cos3x)/(D^2 (D−2)+9(D−2))) =6×((cos3x)/((D−2)(D^2 +9))) =6×(((D+2) cos3x)/((D^2 −4)(D^2 +9))) =(6/((−3^2 −4)))×((−3sin3x+2cos3x)/(D^2 +9)) =((−6)/(13))×((−3sin3x+2cos3x)/(D^2 +9)) =(6/(13))×(((3sin3x−2cos3x))/(D^2 +9)) =(6/(13))×((rsin(3x−θ))/(D^2 +9)) [r=(√(3^2 +2^2 )) =(√(13)) tanθ=(2/3)] p=(6/((√(13)) ))×((cos(3x−θ))/(D^2 +9)) q=(6/(√(13)))×((sin(3x−θ))/(D^2 +9)) p+iq=(6/(√(13)))×(e^(i(3x−θ)) /(D^2 +9)) p+iq=(6/(√(13)))×e^(−iθ) ×(e^(i×3x) /(D^2 +9)) p+iq=(6/(√(13)))×e^(−iθ) ×(e^(i3x) /((D+i3)(D−i3))) p+iq=(6/(√(13)))×(cosθ−isinθ)×(e^(i3x) /((i3+i3)(D+i3−i3)))×1 =(6/(√(13)))×((3/(√(13)))−i×(2/(√(13))))×(((cos3x+isin3x))/(6i))×x =(1/(13))×((3i+2)/i^2 )×(xcos3x+ixsin3x) =((−1)/(13))(i3xcos3x−3xsin3x+2xcos3x+i2xsin3x) =((−1)/(13)){(2xcos3x−3xsin3x)+i(3xcos3x+2xsin3x)} =((−x)/(13))(2cos3x−3sin3x)+((−ix)/(13))(3cos3x+2sin3x) now our answer is related to complex part so answer is Particular intregal is =((−x)/(13))(3cos3x+2sin3x) so complte answer is=C.F+P.I y=C_1 e^(2x) +C_2 e^(i3x) +C_3 e^(−i3x) +((−x)/(13))(3cos3x+2sin3x)](Q56581.png) | ||
| ||