Sum the series: sin^2 (α) + sin^2 (2α) + sin^2 (3α) + ... + sin^2 (nα)


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 56602 by Tawa1 last updated on 19/Mar/19

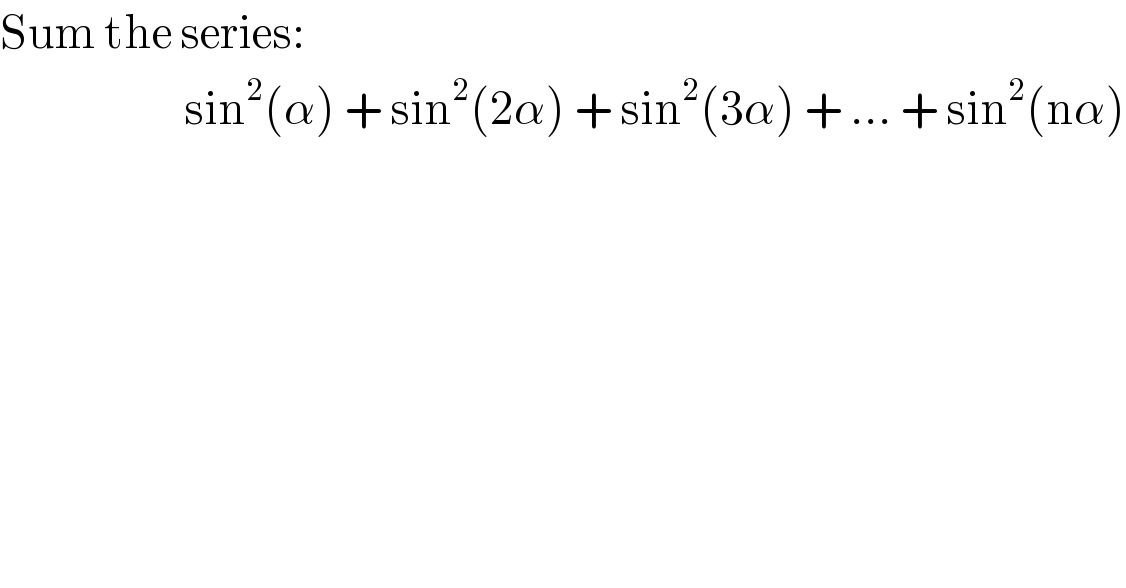
$Sum the series :$ $\sin^{2} (α) + \sin^{2} (2 α) + \sin^{2} (3 α) + . . . + \sin^{2} (n α)$
Commented by maxmathsup by imad last updated on 26/Mar/19
$let S_n =Σ_(k=1) ^n sin^2 (kα) ⇒S_n =Σ_(k=1) ^n ((1−cos(2kα))/2) =(n/2) −(1/2)Σ_(k=1) ^n cos(2kα) but Σ_(k=1) ^n cos(2kα) =Σ_(k=0) ^n cos(2kα)−1 =Re(Σ_(k=0) ^n e^(i2kα) )−1 Σ_(k=0) ^n e^(i2kα) =Σ_(k=0) ^n (e^(i2α) )^k =((1−e^(i2(n+1)α) )/(1−e^(i2α) )) (if e^(i2α) ≠1) =((1−cos2(n+1)α−isin2(n+1)α)/(1−cos(2α)−isin(2α))) = ((2sin^2 (n+1)α −2isin((n+1)α) cos((n+1)α))/(2sin^2 α −2i sinα cosα)) =((−i sin(n+1)α{cos(n+1)α +i sin(n+1)α)/(−isinα{ cosα +isinα})) =((sin(n+1)α)/(sinα)) e^(i(n+1)α) e^(−iα) =((sin(n+1)α)/(sinα)) e^(inα) =((sin(n+1)α)/(sinα)){cos(nα)+isin(nα)} ⇒ Σ_(k=1) ^n cos(2kα) =((sin(n+1)α cos(nα))/(sinα)) −1 ⇒ S_n =(n/2) −(1/2)( ((sin(n+1)α cos(nα))/(sinα)) −1) =((n+1)/2) −((sin(n+1)α cos(nα))/(2sinα)) if e^(i2α) ≠1 .$
$l e t S_{n} = \sum_{k = 1}^{n} {s i n}^{2} (k α) \Rightarrow S_{n} = \sum_{k = 1}^{n} \frac{1 - c o s (2 k α)}{2}$ $= \frac{n}{2} - \frac{1}{2} \sum_{k = 1}^{n} c o s (2 k α) b u t$ $\sum_{k = 1}^{n} c o s (2 k α) = \sum_{k = 0}^{n} c o s (2 k α) - 1 = R e (\sum_{k = 0}^{n} e^{i 2 k α}) - 1$ $\sum_{k = 0}^{n} e^{i 2 k α} = \sum_{k = 0}^{n} {(e^{i 2 α})}^{k} = \frac{1 - e^{i 2 (n + 1) α}}{1 - e^{i 2 α}} (i f e^{i 2 α} \neq 1)$ $= \frac{1 - c o s 2 (n + 1) α - i s i n 2 (n + 1) α}{1 - c o s (2 α) - i s i n (2 α)} = \frac{2 {s i n}^{2} (n + 1) α - 2 i s i n ((n + 1) α) c o s ((n + 1) α)}{2 {s i n}^{2} α - 2 i s i n α c o s α}$ $= \frac{- i s i n (n + 1) α {c o s (n + 1) α + i s i n (n + 1) α}{- i s i n α {c o s α + i s i n α}} = \frac{s i n (n + 1) α}{s i n α} e^{i (n + 1) α} e^{- i α}$ $= \frac{s i n (n + 1) α}{s i n α} e^{i n α} = \frac{s i n (n + 1) α}{s i n α} {c o s (n α) + i s i n (n α)} \Rightarrow$ $\sum_{k = 1}^{n} c o s (2 k α) = \frac{s i n (n + 1) α c o s (n α)}{s i n α} - 1 \Rightarrow$ $S_{n} = \frac{n}{2} - \frac{1}{2} (\frac{s i n (n + 1) α c o s (n α)}{s i n α} - 1) = \frac{n + 1}{2} - \frac{s i n (n + 1) α c o s (n α)}{2 s i n α}$ $i f e^{i 2 α} \neq 1 .$
	Answered by tanmay.chaudhury50@gmail.com last updated on 19/Mar/19

	$T_{n} = {s i n}^{2} (n α)$ $T_{n} = \frac{1 - c o s 2 n α}{2}$ $= \frac{1}{2} - \frac{1}{2} (c o s 2 n α)$ $T_{1} = \frac{1}{2} - \frac{1}{2} (c o s 2 α)$ $T_{2} = \frac{1}{2} - \frac{1}{2} (c o s 4 α)$ $T_{3} = \frac{1}{2} - \frac{1}{2} (c o s 6 α)$ $. . .$ $. . .$ $T_{n} = \frac{1}{2} - \frac{1}{2} (c o s 2 n α)$ $S = n \times \frac{1}{2} - \frac{1}{2} (c o s 2 α + c o s 4 α + c o s 6 α + . . . + c o s 2 n α)$ $S = \frac{n}{2} - \frac{p}{2}$ $p = c o s 2 α + c o s 4 α + c o s 6 α + . . . + c o s 2 n α$ $2 c o s 2 α s i n α = s i n 3 α - s i n α$ $2 c o s 4 α s i n α = s i n 5 α - s i n 3 α$ $2 c o s 6 α s i n α = s i n 7 α - s i n 5 α$ $. . .$ $. . .$ $2 c o s 2 n α s i n α = s i n (2 n + 1) α - s i n (2 n - 1) α$ $a d d t h e m$ $2 s i n α (c o s 2 α + c o s 4 α + . . + c o s 2 n α) = s i n (2 n + 1) α - s i n α$ $2 s i n α \times p = s i n (2 n + 1) α - s i n α$ $p = \frac{s i n (2 n + 1) α - s i n α}{2 s i n α}$ $S o S = \frac{n}{2} - \frac{p}{2}$ $= \frac{n}{2} - \frac{s i n (2 n + 1) α - s i n α}{4 s i n α}$ $p l s c h e c k . . .$
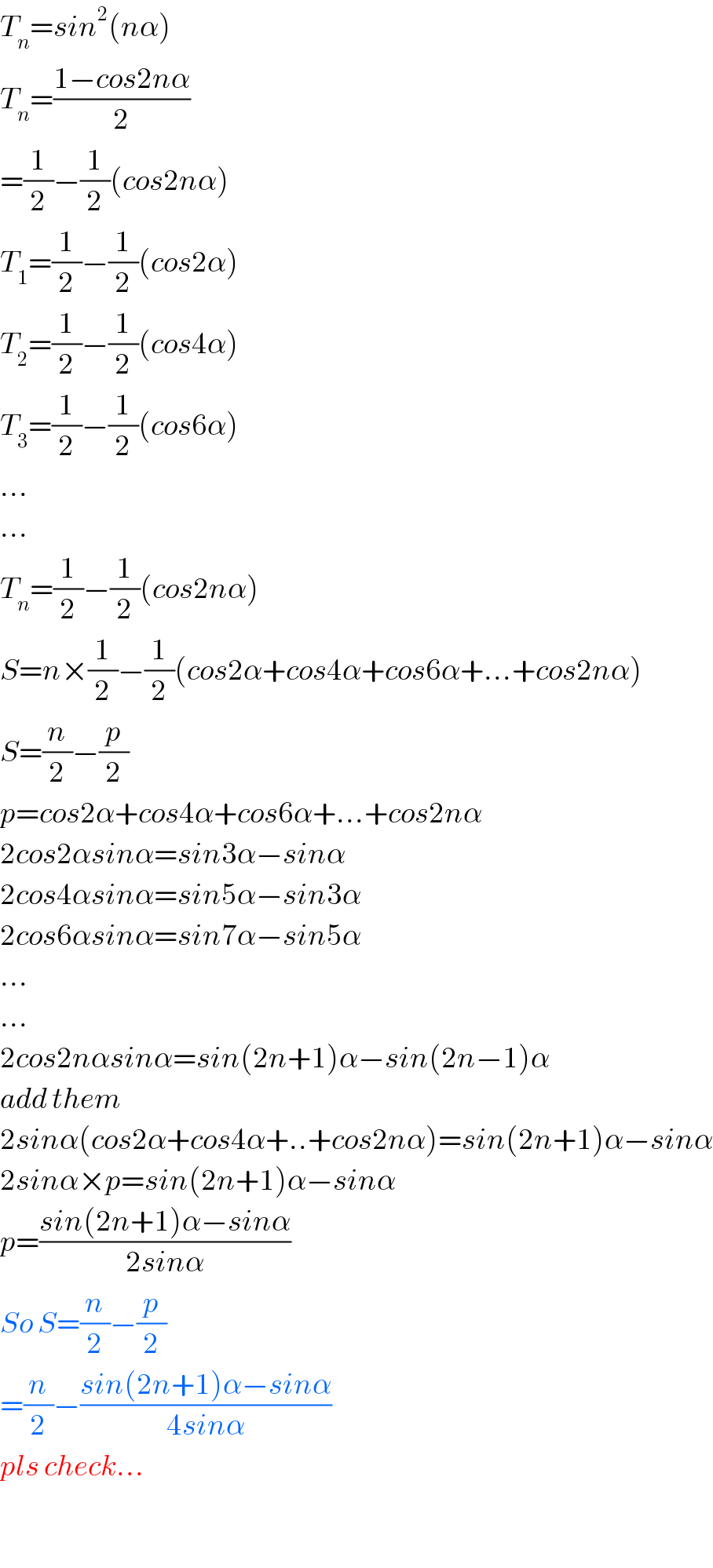
	Commented by maxmathsup by imad last updated on 19/Mar/19

	$b e c a r e f u l α h e r e i s i n r a d i a n n o t i n d e g r e . . .$
	Commented by Tawa1 last updated on 19/Mar/19

	$Thanks sir .$
	Commented by Tawa1 last updated on 19/Mar/19

	$Then it will be stated that where α is in degree, can it ?$
	Commented by Tawa1 last updated on 19/Mar/19

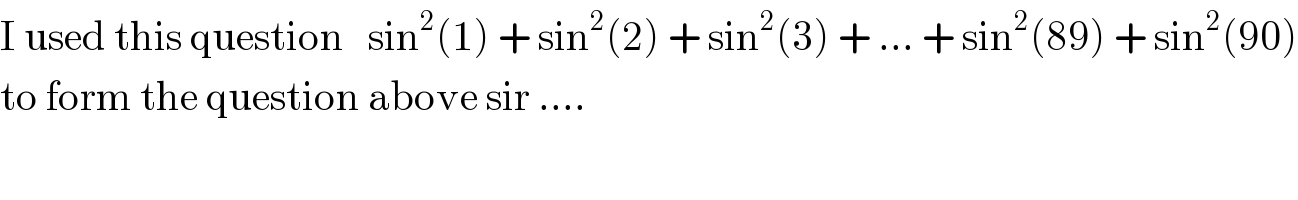
	$I used this question \sin^{2} (1) + \sin^{2} (2) + \sin^{2} (3) + . . . + \sin^{2} (89) + \sin^{2} (90)$ $to form the question above sir . . . .$
	Commented by Tawa1 last updated on 19/Mar/19

	$Correct sir .$ $\sin^{2} (α) + \sin^{2} (2 α) + \sin^{2} (3 α) + . . . + \sin^{2} (n α) = \frac{n}{2} - \frac{\sin (2 n + 1) α - \sin (α)}{4 \sin (α)}$ $where α = 1$ $\sin^{2} (1) + \sin^{2} (2) + \sin^{2} (3) + . . . + \sin^{2} (89) + \sin^{2} (90)$ $= \frac{90}{2} - \frac{\sin [2 (90) + 1] - \sin (1)}{4 \sin (1)}$ $\sin^{2} (1) + \sin^{2} (2) + \sin^{2} (3) + . . . + \sin^{2} (89) + \sin^{2} (90)$ $= \frac{90}{2} - \frac{\sin (180) - \sin (1)}{4 \sin (1)}$ $\sin^{2} (1) + \sin^{2} (2) + \sin^{2} (3) + . . . + \sin^{2} (89) + \sin^{2} (90) = \frac{90}{2} - (- \frac{1}{2})$ $\sin^{2} (1) + \sin^{2} (2) + \sin^{2} (3) + . . . + \sin^{2} (89) + \sin^{2} (90) = 45 + 0.5$ $\sin^{2} (1) + \sin^{2} (2) + \sin^{2} (3) + . . . + \sin^{2} (89) + \sin^{2} (90) = 45.5$ $Same as what you got earlier and sir mrW .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum