Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 56641 by ajfour last updated on 20/Mar/19

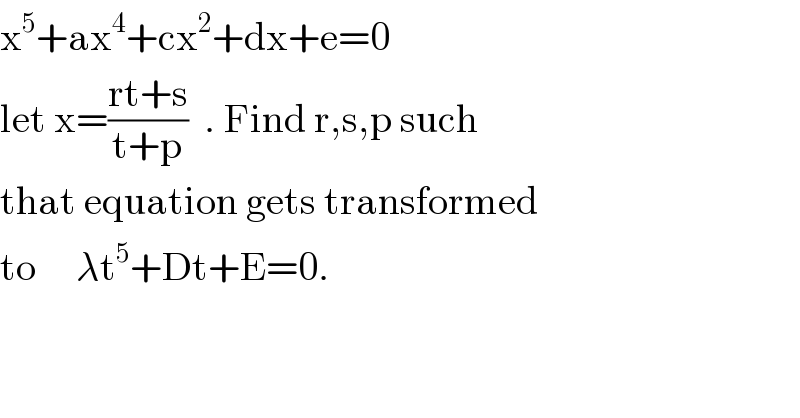
x^5 +ax^4 +cx^2 +dx+e=0 let x=((rt+s)/(t+p)) . Find r,s,p such that equation gets transformed to λt^5 +Dt+E=0.

$$\mathrm{x}^{\mathrm{5}} +\mathrm{ax}^{\mathrm{4}} +\mathrm{cx}^{\mathrm{2}} +\mathrm{dx}+\mathrm{e}=\mathrm{0} \\ $$$$\mathrm{let}\:\mathrm{x}=\frac{\mathrm{rt}+\mathrm{s}}{\mathrm{t}+\mathrm{p}}\:\:.\:\mathrm{Find}\:\mathrm{r},\mathrm{s},\mathrm{p}\:\mathrm{such} \\ $$$$\mathrm{that}\:\mathrm{equation}\:\mathrm{gets}\:\mathrm{transformed} \\ $$$$\mathrm{to}\:\:\:\:\:\lambda\mathrm{t}^{\mathrm{5}} +\mathrm{Dt}+\mathrm{E}=\mathrm{0}. \\ $$

Commented by ajfour last updated on 20/Mar/19

Granted this is done, we need to see if the quintic can perhaps now be solved.. let x^5 +kx+q=0 equivalently (x^2 +fx+g)(x^3 +hx^2 +mx+n)=0 ⇒ x^5 +(h+f)x^4 +(m+fh+g)x^3 + (n+fm+gh)x^2 +(fn+gm)x+gn=0 ⇒ h+f=0 m+fh+g=0 n+fm+gh=0 ...(i) fn+gm=k ....(ii) gn=q from (i) [ (q/g)−h(h^2 −g)+gh=0 ]×h & from (ii) −((hq)/g)+g(h^2 −g)=k Adding 3gh^2 +g^2 −h^4 =k ]×g ...(I) & gh^3 −2g^2 h = q ]×h Adding g^2 h^2 +g^3 = gk+hq ...(II) from (I) h^2 = ((3g±(√(9g^2 −4(k−g^2 ))))/2) ⇒ h^2 = ((3g)/2)±((√(13g^2 −4k))/2) while from (II) h= ((q±(√(q^2 −4g^3 (g^2 −k))))/(2g^2 )) ⇒ ((3g)/2)±((√(13g^2 −4k))/2) = [((q±(√(q^2 −4g^3 (g^2 −k))))/(2g^2 ))]^2 +× ?%%/ Degree 5 is degree 5//

$$\mathrm{Granted}\:\mathrm{this}\:\mathrm{is}\:\mathrm{done},\:\mathrm{we}\:\mathrm{need}\:\mathrm{to} \\ $$$$\mathrm{see}\:\mathrm{if}\:\mathrm{the}\:\mathrm{quintic}\:\mathrm{can}\:\mathrm{perhaps}\:\mathrm{now} \\ $$$$\mathrm{be}\:\mathrm{solved}.. \\ $$$$\mathrm{let} \\ $$$$\:\:\:\mathrm{x}^{\mathrm{5}} +\mathrm{kx}+\mathrm{q}=\mathrm{0} \\ $$$$\mathrm{equivalently} \\ $$$$\:\:\left(\mathrm{x}^{\mathrm{2}} +\mathrm{fx}+\mathrm{g}\right)\left(\mathrm{x}^{\mathrm{3}} +\mathrm{hx}^{\mathrm{2}} +\mathrm{mx}+\mathrm{n}\right)=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\mathrm{x}^{\mathrm{5}} +\left(\mathrm{h}+\mathrm{f}\right)\mathrm{x}^{\mathrm{4}} +\left(\mathrm{m}+\mathrm{fh}+\mathrm{g}\right)\mathrm{x}^{\mathrm{3}} + \\ $$$$\:\:\left(\mathrm{n}+\mathrm{fm}+\mathrm{gh}\right)\mathrm{x}^{\mathrm{2}} +\left(\mathrm{fn}+\mathrm{gm}\right)\mathrm{x}+\mathrm{gn}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\boldsymbol{\mathrm{h}}+\boldsymbol{\mathrm{f}}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\boldsymbol{\mathrm{m}}+\boldsymbol{\mathrm{fh}}+\boldsymbol{\mathrm{g}}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\boldsymbol{\mathrm{n}}+\boldsymbol{\mathrm{fm}}+\boldsymbol{\mathrm{gh}}=\mathrm{0}\:\:\:\:\:...\left(\mathrm{i}\right) \\ $$$$\:\:\:\:\:\:\:\boldsymbol{\mathrm{fn}}+\boldsymbol{\mathrm{gm}}=\boldsymbol{\mathrm{k}}\:\:\:\:\:\:\:\:\:\:\:\:....\left(\mathrm{ii}\right) \\ $$$$\:\:\:\:\:\:\:\boldsymbol{\mathrm{gn}}=\boldsymbol{\mathrm{q}} \\ $$$$\:\:\:\mathrm{from}\:\left(\mathrm{i}\right) \\ $$$$\:\:\:\left[\:\frac{\mathrm{q}}{\mathrm{g}}−\mathrm{h}\left(\mathrm{h}^{\mathrm{2}} −\mathrm{g}\right)+\mathrm{gh}=\mathrm{0}\:\:\:\right]×\mathrm{h} \\ $$$$\&\:\mathrm{from}\:\left(\mathrm{ii}\right) \\ $$$$\:\:\:\:−\frac{\mathrm{hq}}{\mathrm{g}}+\mathrm{g}\left(\mathrm{h}^{\mathrm{2}} −\mathrm{g}\right)=\mathrm{k} \\ $$$$\mathrm{Adding} \\ $$$$\left.\:\:\:\:\mathrm{3gh}^{\mathrm{2}} +\mathrm{g}^{\mathrm{2}} −\mathrm{h}^{\mathrm{4}} =\mathrm{k}\:\:\:\right]×\mathrm{g}\:\:\:\:\:\:...\left(\mathrm{I}\right)\:\:\:\:\:\& \\ $$$$\left.\:\:\:\:\:\mathrm{gh}^{\mathrm{3}} −\mathrm{2g}^{\mathrm{2}} \mathrm{h}\:=\:\mathrm{q}\:\:\:\:\:\:\right]×\mathrm{h} \\ $$$$\mathrm{Adding} \\ $$$$\:\:\:\:\:\mathrm{g}^{\mathrm{2}} \mathrm{h}^{\mathrm{2}} +\mathrm{g}^{\mathrm{3}} =\:\mathrm{gk}+\mathrm{hq}\:\:\:\:\:\:\:\:\:\:\:\:\:\:...\left(\mathrm{II}\right) \\ $$$$\mathrm{from}\:\left(\mathrm{I}\right) \\ $$$$\:\:\:\:\mathrm{h}^{\mathrm{2}} \:=\:\frac{\mathrm{3g}\pm\sqrt{\mathrm{9g}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{k}−\mathrm{g}^{\mathrm{2}} \right)}}{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\:\mathrm{h}^{\mathrm{2}} \:=\:\frac{\mathrm{3g}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{13g}^{\mathrm{2}} −\mathrm{4k}}}{\mathrm{2}} \\ $$$$\mathrm{while}\:\mathrm{from}\:\left(\mathrm{II}\right) \\ $$$$\:\:\:\:\:\:\:\:\mathrm{h}=\:\frac{\mathrm{q}\pm\sqrt{\mathrm{q}^{\mathrm{2}} −\mathrm{4g}^{\mathrm{3}} \left(\mathrm{g}^{\mathrm{2}} −\mathrm{k}\right)}}{\mathrm{2g}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\frac{\mathrm{3g}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{13g}^{\mathrm{2}} −\mathrm{4k}}}{\mathrm{2}}\:=\:\left[\frac{\mathrm{q}\pm\sqrt{\mathrm{q}^{\mathrm{2}} −\mathrm{4g}^{\mathrm{3}} \left(\mathrm{g}^{\mathrm{2}} −\mathrm{k}\right)}}{\mathrm{2g}^{\mathrm{2}} }\right]^{\mathrm{2}} \\ $$$$ \\ $$$$\:\:\:+×\:?\%\%/\:\mathrm{Degree}\:\mathrm{5}\:\mathrm{is}\:\mathrm{degree}\:\mathrm{5}// \\ $$

Commented by Tawa1 last updated on 20/Mar/19

Wow, God bless you sir.

$$\mathrm{Wow},\:\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Answered by ajfour last updated on 20/Mar/19

(rt+s)^5 +a(rt+s)^4 (t+p)+c(rt+s)^2 (t+p)^3 +d(rt+s)(t+p)^4 +(t+p)^5 =0 r^5 t^5 +5r^4 st^4 +10r^3 s^2 t^3 +10r^2 s^3 t^2 + +5rs^4 t+s^5 +a(r^4 t^4 +4r^3 st^3 +6r^2 s^2 t^2 +4rs^3 t+s^4 )(t+p) +c(r^2 t^2 +2rst+s^2 )(t^3 +3pt^2 +3p^2 t+p^3 ) +d(rt+s)(t^4 +4pt^3 +6p^2 t^2 +4p^3 t+p^4 ) +e(t^5 +5pt^4 +10p^2 t^3 +10p^3 t^2 +5p^4 t+p^5 ) = 0 ⇒ (r^5 +ar^4 +cr^2 +dr+e)t^5 + (5r^4 s+apr^4 +4ar^3 s+3cpr^2 +2crs+ 4dpr+ds+5ep)t^4 + (10r^3 s^2 +4apr^3 s+6ar^2 s^2 +3cp^2 r^2 +6cprs+cs^2 +6dp^2 r+4dps+10ep^2 )t^3 (10r^2 s^3 +6apr^2 s^2 +4ars^3 +cp^3 r^2 +6cp^2 rs +3cps^2 +4dp^3 r+6dp^2 s+10ep^3 )t^2 +Dt+E = 0 If coefficients of t^4 ,t^3 ,t^2 are to be zero; then 5r^4 s+apr^4 +4ar^3 s+3cpr^2 +2crs+ 4dpr+ds+5pe = 0 & 10r^3 s^2 +4apr^3 s+6ar^2 s^2 +3cp^2 r^2 + 6cprs+cs^2 +6dp^2 r+4dps+10ep^2 =0 & 10r^2 s^3 +6apr^2 s^2 +4ars^3 +cp^3 r^2 +6cp^2 rs +3cps^2 +4dp^3 r+6dp^2 s+10ep^3 =0 .....

$$\left(\mathrm{rt}+\mathrm{s}\right)^{\mathrm{5}} +\mathrm{a}\left(\mathrm{rt}+\mathrm{s}\right)^{\mathrm{4}} \left(\mathrm{t}+\mathrm{p}\right)+\mathrm{c}\left(\mathrm{rt}+\mathrm{s}\right)^{\mathrm{2}} \left(\mathrm{t}+\mathrm{p}\right)^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{d}\left(\mathrm{rt}+\mathrm{s}\right)\left(\mathrm{t}+\mathrm{p}\right)^{\mathrm{4}} +\left(\mathrm{t}+\mathrm{p}\right)^{\mathrm{5}} =\mathrm{0} \\ $$$$\mathrm{r}^{\mathrm{5}} \mathrm{t}^{\mathrm{5}} +\mathrm{5r}^{\mathrm{4}} \mathrm{st}^{\mathrm{4}} +\mathrm{10r}^{\mathrm{3}} \mathrm{s}^{\mathrm{2}} \mathrm{t}^{\mathrm{3}} +\mathrm{10r}^{\mathrm{2}} \mathrm{s}^{\mathrm{3}} \mathrm{t}^{\mathrm{2}} + \\ $$$$\:\:\:\:\:\:\:\:\:+\mathrm{5rs}^{\mathrm{4}} \mathrm{t}+\mathrm{s}^{\mathrm{5}} \\ $$$$+\mathrm{a}\left(\mathrm{r}^{\mathrm{4}} \mathrm{t}^{\mathrm{4}} +\mathrm{4r}^{\mathrm{3}} \mathrm{st}^{\mathrm{3}} +\mathrm{6r}^{\mathrm{2}} \mathrm{s}^{\mathrm{2}} \mathrm{t}^{\mathrm{2}} +\mathrm{4rs}^{\mathrm{3}} \mathrm{t}+\mathrm{s}^{\mathrm{4}} \right)\left(\mathrm{t}+\mathrm{p}\right) \\ $$$$+\mathrm{c}\left(\mathrm{r}^{\mathrm{2}} \mathrm{t}^{\mathrm{2}} +\mathrm{2rst}+\mathrm{s}^{\mathrm{2}} \right)\left(\mathrm{t}^{\mathrm{3}} +\mathrm{3pt}^{\mathrm{2}} +\mathrm{3p}^{\mathrm{2}} \mathrm{t}+\mathrm{p}^{\mathrm{3}} \right) \\ $$$$+\mathrm{d}\left(\mathrm{rt}+\mathrm{s}\right)\left(\mathrm{t}^{\mathrm{4}} +\mathrm{4pt}^{\mathrm{3}} +\mathrm{6p}^{\mathrm{2}} \mathrm{t}^{\mathrm{2}} +\mathrm{4p}^{\mathrm{3}} \mathrm{t}+\mathrm{p}^{\mathrm{4}} \right) \\ $$$$+\mathrm{e}\left(\mathrm{t}^{\mathrm{5}} +\mathrm{5pt}^{\mathrm{4}} +\mathrm{10p}^{\mathrm{2}} \mathrm{t}^{\mathrm{3}} +\mathrm{10p}^{\mathrm{3}} \mathrm{t}^{\mathrm{2}} +\mathrm{5p}^{\mathrm{4}} \mathrm{t}+\mathrm{p}^{\mathrm{5}} \right) \\ $$$$\:=\:\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\:\:\:\:\left(\mathrm{r}^{\mathrm{5}} +\mathrm{ar}^{\mathrm{4}} +\mathrm{cr}^{\mathrm{2}} +\mathrm{dr}+\mathrm{e}\right)\mathrm{t}^{\mathrm{5}} + \\ $$$$\:\left(\mathrm{5r}^{\mathrm{4}} \mathrm{s}+\mathrm{apr}^{\mathrm{4}} +\mathrm{4ar}^{\mathrm{3}} \mathrm{s}+\mathrm{3cpr}^{\mathrm{2}} +\mathrm{2crs}+\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{4dpr}+\mathrm{ds}+\mathrm{5ep}\right)\mathrm{t}^{\mathrm{4}} + \\ $$$$\:\:\left(\mathrm{10r}^{\mathrm{3}} \mathrm{s}^{\mathrm{2}} +\mathrm{4apr}^{\mathrm{3}} \mathrm{s}+\mathrm{6ar}^{\mathrm{2}} \mathrm{s}^{\mathrm{2}} +\mathrm{3cp}^{\mathrm{2}} \mathrm{r}^{\mathrm{2}} \right. \\ $$$$\left.\:\:\:+\mathrm{6cprs}+\mathrm{cs}^{\mathrm{2}} +\mathrm{6dp}^{\mathrm{2}} \mathrm{r}+\mathrm{4dps}+\mathrm{10ep}^{\mathrm{2}} \right)\mathrm{t}^{\mathrm{3}} \\ $$$$\:\left(\mathrm{10r}^{\mathrm{2}} \mathrm{s}^{\mathrm{3}} +\mathrm{6apr}^{\mathrm{2}} \mathrm{s}^{\mathrm{2}} +\mathrm{4ars}^{\mathrm{3}} +\mathrm{cp}^{\mathrm{3}} \mathrm{r}^{\mathrm{2}} +\mathrm{6cp}^{\mathrm{2}} \mathrm{rs}\right. \\ $$$$\left.\:\:\:\:\:+\mathrm{3cps}^{\mathrm{2}} +\mathrm{4dp}^{\mathrm{3}} \mathrm{r}+\mathrm{6dp}^{\mathrm{2}} \mathrm{s}+\mathrm{10ep}^{\mathrm{3}} \right)\mathrm{t}^{\mathrm{2}} \\ $$$$\:\:\:+\mathrm{Dt}+\mathrm{E}\:=\:\mathrm{0} \\ $$$$\mathrm{If}\:\mathrm{coefficients}\:\mathrm{of}\:\mathrm{t}^{\mathrm{4}} ,\mathrm{t}^{\mathrm{3}} ,\mathrm{t}^{\mathrm{2}} \:\mathrm{are}\:\mathrm{to}\:\mathrm{be}\:\mathrm{zero}; \\ $$$$\mathrm{then} \\ $$$$\:\:\mathrm{5r}^{\mathrm{4}} \mathrm{s}+\mathrm{apr}^{\mathrm{4}} +\mathrm{4ar}^{\mathrm{3}} \mathrm{s}+\mathrm{3cpr}^{\mathrm{2}} +\mathrm{2crs}+ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{4dpr}+\mathrm{ds}+\mathrm{5pe}\:=\:\mathrm{0} \\ $$$$\& \\ $$$$\mathrm{10r}^{\mathrm{3}} \mathrm{s}^{\mathrm{2}} +\mathrm{4apr}^{\mathrm{3}} \mathrm{s}+\mathrm{6ar}^{\mathrm{2}} \mathrm{s}^{\mathrm{2}} +\mathrm{3cp}^{\mathrm{2}} \mathrm{r}^{\mathrm{2}} + \\ $$$$\:\:\:\mathrm{6cprs}+\mathrm{cs}^{\mathrm{2}} +\mathrm{6dp}^{\mathrm{2}} \mathrm{r}+\mathrm{4dps}+\mathrm{10ep}^{\mathrm{2}} =\mathrm{0} \\ $$$$\& \\ $$$$\mathrm{10r}^{\mathrm{2}} \mathrm{s}^{\mathrm{3}} +\mathrm{6apr}^{\mathrm{2}} \mathrm{s}^{\mathrm{2}} +\mathrm{4ars}^{\mathrm{3}} +\mathrm{cp}^{\mathrm{3}} \mathrm{r}^{\mathrm{2}} +\mathrm{6cp}^{\mathrm{2}} \mathrm{rs} \\ $$$$\:+\mathrm{3cps}^{\mathrm{2}} +\mathrm{4dp}^{\mathrm{3}} \mathrm{r}+\mathrm{6dp}^{\mathrm{2}} \mathrm{s}+\mathrm{10ep}^{\mathrm{3}} =\mathrm{0} \\ $$$$..... \\ $$

Commented by Tawa1 last updated on 20/Mar/19

Wow, God bless you sir. Weldone

$$\mathrm{Wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{Weldone} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com