Question Number 56643 by Sr@2004 last updated on 20/Mar/19
Commented by Sr@2004 last updated on 20/Mar/19
$${please}\:{solve}\:\mathrm{6},\mathrm{7},\mathrm{8},\mathrm{9} \\ $$
Commented by malwaan last updated on 21/Mar/19
$$\mathrm{and}\:\mathrm{10}\:? \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 20/Mar/19
$${cosec}\alpha+{cot}\alpha=\mathrm{2}+\sqrt{\mathrm{5}}\: \\ $$$${cosec}^{\mathrm{2}} \alpha−{cot}^{\mathrm{2}} \alpha=\mathrm{1} \\ $$$$\left({cosec}\alpha+{cot}\alpha\right)\left({cosec}\alpha−{cot}\alpha\right)=\mathrm{1} \\ $$$${cosec}\alpha−{cot}\alpha=\frac{\mathrm{1}}{\sqrt{\mathrm{5}}\:+\mathrm{2}}=\frac{\sqrt{\mathrm{5}}\:−\mathrm{2}}{\left(\sqrt{\mathrm{5}}\:+\mathrm{2}\right)\left(\sqrt{\mathrm{5}}\:−\mathrm{2}\right)}=\frac{\sqrt{\mathrm{5}}\:−\mathrm{2}}{\mathrm{1}} \\ $$$${cosec}\alpha+{cot}\alpha=\sqrt{\mathrm{5}}\:+\mathrm{2} \\ $$$${cosec}\alpha−{cot}\alpha=\sqrt{\mathrm{5}}\:−\mathrm{2} \\ $$$$\mathrm{2}{cosec}\alpha=\mathrm{2}\sqrt{\mathrm{5}}\: \\ $$$${sin}\alpha=\frac{\mathrm{1}}{\sqrt{\mathrm{5}}}\rightarrow{cos}^{\mathrm{2}} \alpha=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5}}=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$${cos}\alpha=\frac{\mathrm{2}}{\sqrt{\mathrm{5}}} \\ $$$$ \\ $$$$ \\ $$
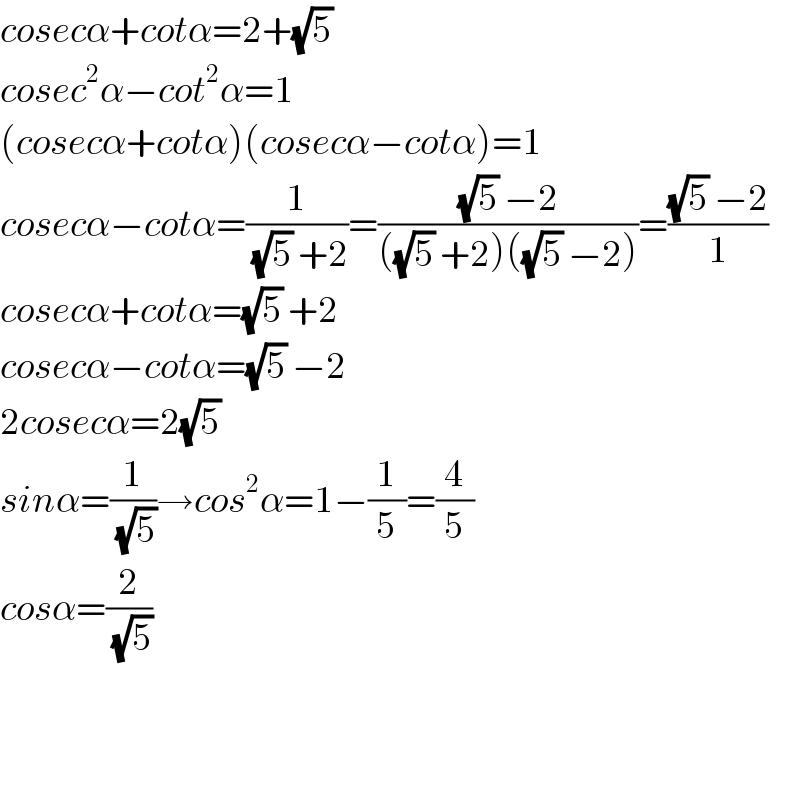
Answered by tanmay.chaudhury50@gmail.com last updated on 20/Mar/19
![((sin^4 θ)/x)+((cos^4 θ)/y)=(1/(x+y)) let a=sin^2 θ (a^2 /x)+(((1−a)^2 )/y)=(1/(x+y)) ya^2 +x(1−2a+a^2 )=((xy)/(x+y)) a^2 (xy+y^2 )+(1−2a+a^2 )(x^2 +xy)=xy a^2 xy+a^2 y^2 +x^2 +xy−2ax^2 −2axy+a^2 x^2 +a^2 xy=xy a^2 (xy+y^2 +x^2 +xy)−2a(x^2 +xy)+x^2 =0 a^2 (x+y)^2 −2a(x+y)x+x^2 =0 {a(x+y)−x}^2 =0 a(x+y)=x a=(x/(x+y))→sin^2 θ=(x/(x+y))[a=sin^2 θ] cos^2 θ=1−sin^2 θ=1−(x/(x+y)) cos^2 θ=(y/((x+y))) now ((sin^(2m+2) θ)/x^m )+((cos^(2m+2) θ)/y^m ) =((((x/(x+y)))^(m+1) )/x^m )+((((y/(x+y)))^(m+1) )/y^m ) =(x/((x+y)^(m+1) ))+(y/((x+y)^(m+1) )) =((x+y)/((x+y)^(m+1) )) =(1/((x+y)^m )) proved](Q56648.png)
$$\frac{{sin}^{\mathrm{4}} \theta}{{x}}+\frac{{cos}^{\mathrm{4}} \theta}{{y}}=\frac{\mathrm{1}}{{x}+{y}} \\ $$$${let}\:{a}={sin}^{\mathrm{2}} \theta \\ $$$$\frac{{a}^{\mathrm{2}} }{{x}}+\frac{\left(\mathrm{1}−{a}\right)^{\mathrm{2}} }{{y}}=\frac{\mathrm{1}}{{x}+{y}} \\ $$$${ya}^{\mathrm{2}} +{x}\left(\mathrm{1}−\mathrm{2}{a}+{a}^{\mathrm{2}} \right)=\frac{{xy}}{{x}+{y}} \\ $$$${a}^{\mathrm{2}} \left({xy}+{y}^{\mathrm{2}} \right)+\left(\mathrm{1}−\mathrm{2}{a}+{a}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} +{xy}\right)={xy} \\ $$$${a}^{\mathrm{2}} {xy}+{a}^{\mathrm{2}} {y}^{\mathrm{2}} +{x}^{\mathrm{2}} +{xy}−\mathrm{2}{ax}^{\mathrm{2}} −\mathrm{2}{axy}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} +{a}^{\mathrm{2}} {xy}={xy} \\ $$$${a}^{\mathrm{2}} \left({xy}+{y}^{\mathrm{2}} +{x}^{\mathrm{2}} +{xy}\right)−\mathrm{2}{a}\left({x}^{\mathrm{2}} +{xy}\right)+{x}^{\mathrm{2}} =\mathrm{0} \\ $$$${a}^{\mathrm{2}} \left({x}+{y}\right)^{\mathrm{2}} −\mathrm{2}{a}\left({x}+{y}\right){x}+{x}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left\{{a}\left({x}+{y}\right)−{x}\right\}^{\mathrm{2}} =\mathrm{0} \\ $$$${a}\left({x}+{y}\right)={x} \\ $$$${a}=\frac{{x}}{{x}+{y}}\rightarrow{sin}^{\mathrm{2}} \theta=\frac{{x}}{{x}+{y}}\left[{a}={sin}^{\mathrm{2}} \theta\right] \\ $$$${cos}^{\mathrm{2}} \theta=\mathrm{1}−{sin}^{\mathrm{2}} \theta=\mathrm{1}−\frac{{x}}{{x}+{y}} \\ $$$${cos}^{\mathrm{2}} \theta=\frac{{y}}{\left({x}+{y}\right)} \\ $$$${now} \\ $$$$\frac{{sin}^{\mathrm{2}{m}+\mathrm{2}} \theta}{{x}^{{m}} }+\frac{{cos}^{\mathrm{2}{m}+\mathrm{2}} \theta}{{y}^{{m}} } \\ $$$$=\frac{\left(\frac{{x}}{{x}+{y}}\right)^{{m}+\mathrm{1}} }{{x}^{{m}} }+\frac{\left(\frac{{y}}{{x}+{y}}\right)^{{m}+\mathrm{1}} }{{y}^{{m}} } \\ $$$$=\frac{{x}}{\left({x}+{y}\right)^{{m}+\mathrm{1}} }+\frac{{y}}{\left({x}+{y}\right)^{{m}+\mathrm{1}} } \\ $$$$=\frac{{x}+{y}}{\left({x}+{y}\right)^{{m}+\mathrm{1}} } \\ $$$$=\frac{\mathrm{1}}{\left({x}+{y}\right)^{{m}} }\:{proved} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 20/Mar/19
![tanA=ntanB sinA=msinB ((sinA)/(sinB))=m ((cosecB)/(cosecA))=m ((1+cot^2 B)/(1+cot^2 A))=m^2 [tanB=((tanA)/n)] ((1+(n^2 /(tan^2 A)))/(1+(1/(tan^2 A))))=m^2 ((tan^2 A+n^2 )/(1+tan^2 A))=m^2 tan^2 A+n^2 =m^2 +m^2 tan^2 A tan^2 A(1−m^2 )=m^2 −n^2 tan^2 A=((m^2 −n^2 )/(1−m^2 )) 1+tan^2 A=((m^2 −n^2 )/(1−m^2 ))+1 sec^2 A=((1−n^2 )/(1−m^2 )) cos^2 A=((1−m^2 )/(1−n^2 )) cos^2 A=((m^2 −2)/(n^2 −1))](Q56649.png)
$${tanA}={ntanB} \\ $$$${sinA}={msinB} \\ $$$$\frac{{sinA}}{{sinB}}={m} \\ $$$$\frac{{cosecB}}{{cosecA}}={m} \\ $$$$\frac{\mathrm{1}+{cot}^{\mathrm{2}} {B}}{\mathrm{1}+{cot}^{\mathrm{2}} {A}}={m}^{\mathrm{2}} \:\left[{tanB}=\frac{{tanA}}{{n}}\right] \\ $$$$\frac{\mathrm{1}+\frac{{n}^{\mathrm{2}} }{{tan}^{\mathrm{2}} {A}}}{\mathrm{1}+\frac{\mathrm{1}}{{tan}^{\mathrm{2}} {A}}}={m}^{\mathrm{2}} \\ $$$$\frac{{tan}^{\mathrm{2}} {A}+{n}^{\mathrm{2}} }{\mathrm{1}+{tan}^{\mathrm{2}} {A}}={m}^{\mathrm{2}} \\ $$$${tan}^{\mathrm{2}} {A}+{n}^{\mathrm{2}} ={m}^{\mathrm{2}} +{m}^{\mathrm{2}} {tan}^{\mathrm{2}} {A} \\ $$$${tan}^{\mathrm{2}} {A}\left(\mathrm{1}−{m}^{\mathrm{2}} \right)={m}^{\mathrm{2}} −{n}^{\mathrm{2}} \\ $$$${tan}^{\mathrm{2}} {A}=\frac{{m}^{\mathrm{2}} −{n}^{\mathrm{2}} }{\mathrm{1}−{m}^{\mathrm{2}} } \\ $$$$\mathrm{1}+{tan}^{\mathrm{2}} {A}=\frac{{m}^{\mathrm{2}} −{n}^{\mathrm{2}} }{\mathrm{1}−{m}^{\mathrm{2}} }+\mathrm{1} \\ $$$${sec}^{\mathrm{2}} {A}=\frac{\mathrm{1}−{n}^{\mathrm{2}} }{\mathrm{1}−{m}^{\mathrm{2}} } \\ $$$${cos}^{\mathrm{2}} {A}=\frac{\mathrm{1}−{m}^{\mathrm{2}} }{\mathrm{1}−{n}^{\mathrm{2}} } \\ $$$${cos}^{\mathrm{2}} {A}=\frac{{m}^{\mathrm{2}} −\mathrm{2}}{{n}^{\mathrm{2}} −\mathrm{1}} \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 20/Mar/19
![asinx=bcosx=((2ctanx)/(1−tan^2 x))=k(assumed) a=(k/(sinx)) b=(k/(cosx)) c=(k/((2tanx)/(1−tan^2 x)))→(k/(tan2x)) (a/b)=((cosx)/(sinx))→((a^2 −b^2 )/(a^2 +b^2 ))=((cos^2 x−sin^2 x)/(cos^2 x+sin^2 x))=cos2x now (((a^2 −b^2 )^2 )/(a^2 +b^2 )) =(a^2 −b^2 )×cos2x =((k^2 /(sin^2 x))−(k^2 /(cos^2 x)))×cos2x =k^2 (((cos^2 x−sin^2 x)/(sin^2 xcos^2 x)))cos2x =((4k^2 ×cos2x×cos2x)/(4sin^2 xcos^2 x)) =4k^2 ×((cos^2 2x)/((2sinxcosx)^2 )) =4k^2 ×((cos^2 2x)/(sin^2 2x)) =((4k^2 )/(tan^2 2x)) =4c^2 [(k/(tan2x))=c]](Q56654.png)
$${asinx}={bcosx}=\frac{\mathrm{2}{ctanx}}{\mathrm{1}−{tan}^{\mathrm{2}} {x}}={k}\left({assumed}\right) \\ $$$${a}=\frac{{k}}{{sinx}}\:\:\:{b}=\frac{{k}}{{cosx}}\:\:\:\:{c}=\frac{{k}}{\frac{\mathrm{2}{tanx}}{\mathrm{1}−{tan}^{\mathrm{2}} {x}}}\rightarrow\frac{{k}}{{tan}\mathrm{2}{x}} \\ $$$$\frac{{a}}{{b}}=\frac{{cosx}}{{sinx}}\rightarrow\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }=\frac{{cos}^{\mathrm{2}} {x}−{sin}^{\mathrm{2}} {x}}{{cos}^{\mathrm{2}} {x}+{sin}^{\mathrm{2}} {x}}={cos}\mathrm{2}{x} \\ $$$${now}\:\frac{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$=\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)×{cos}\mathrm{2}{x} \\ $$$$=\left(\frac{{k}^{\mathrm{2}} }{{sin}^{\mathrm{2}} {x}}−\frac{{k}^{\mathrm{2}} }{{cos}^{\mathrm{2}} {x}}\right)×{cos}\mathrm{2}{x} \\ $$$$={k}^{\mathrm{2}} \left(\frac{{cos}^{\mathrm{2}} {x}−{sin}^{\mathrm{2}} {x}}{{sin}^{\mathrm{2}} {xcos}^{\mathrm{2}} {x}}\right){cos}\mathrm{2}{x} \\ $$$$=\frac{\mathrm{4}{k}^{\mathrm{2}} ×{cos}\mathrm{2}{x}×{cos}\mathrm{2}{x}}{\mathrm{4}{sin}^{\mathrm{2}} {xcos}^{\mathrm{2}} {x}} \\ $$$$=\mathrm{4}{k}^{\mathrm{2}} ×\frac{{cos}^{\mathrm{2}} \mathrm{2}{x}}{\left(\mathrm{2}{sinxcosx}\right)^{\mathrm{2}} } \\ $$$$=\mathrm{4}{k}^{\mathrm{2}} ×\frac{{cos}^{\mathrm{2}} \mathrm{2}{x}}{{sin}^{\mathrm{2}} \mathrm{2}{x}} \\ $$$$=\frac{\mathrm{4}{k}^{\mathrm{2}} }{{tan}^{\mathrm{2}} \mathrm{2}{x}} \\ $$$$=\mathrm{4}{c}^{\mathrm{2}} \:\:\left[\frac{{k}}{{tan}\mathrm{2}{x}}={c}\right] \\ $$
Commented by Sr@2004 last updated on 22/Mar/19
$${sir}\:{i}\:{cannot}\:{understand} \\ $$