Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 5672 by sanusihammed last updated on 23/May/16

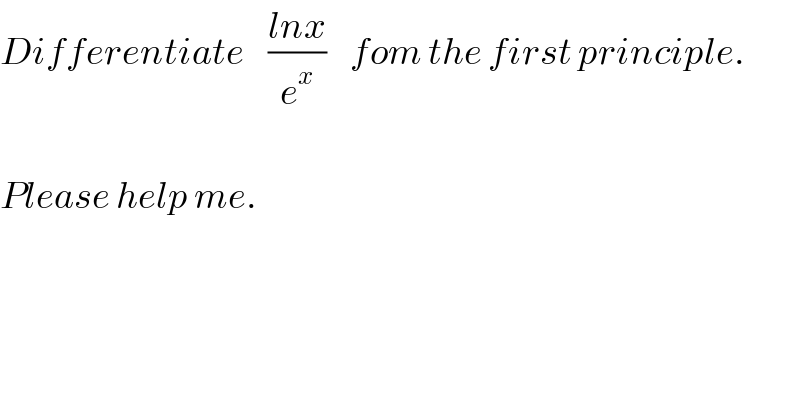
Differentiate ((lnx)/e^x ) fom the first principle. Please help me.

$${Differentiate}\:\:\:\:\frac{{lnx}}{{e}^{{x}} }\:\:\:\:{fom}\:{the}\:{first}\:{principle}. \\ $$$$ \\ $$$${Please}\:{help}\:{me}. \\ $$

Answered by Yozzii last updated on 23/May/16

Let y=((lnx)/e^x ). From first principles (dy/dx)=lim_(h→0) ((f(x+h)−f(x))/h) =lim_(h→0) ((e^(−x−h) ln(x+h)−e^(−x) lnx)/h) =lim_(h→0) (((ln(x+h))/(he^(x+h) ))−((lnx)/(he^x ))) =lim_(h→0) ((ln(x+h)−e^h lnx)/(he^x e^h )) =e^(−x) lim_(h→0) (1/(he^h ))(ln(x+h)−lnx^e^h ) =e^(−x) lim_(h→0) (1/(he^h ))ln((x+h)/x^e^h ) (dy/dx)=e^(−x) lim_(h→0) ln(x^(1−e^h ) +(h/x^e^h ))^(1/he^h ) ln(dy/dx)=ln{e^(−x) }+ln(lim_(h→0) {(1/e^h )ln[(x^(1−e^h ) +(h/x^e^h ))^(1/h) ]}) ln(dy/dx)=−x+ln(lim_(h→0) (1/h)lnx^(1−e^h ) (1+(h/x))) ln(dy/dx)=−x+ln(lim_(h→0) (((1−e^h )/h)lnx+(1/h)ln(1+(h/x)))) • e is a number such that for u being any number, e^u =1+u+(u^2 /(2!))+(u^3 /(3!))+...+(u^n /(n!))+... • For j∈(−1,1] one can write ln(1+j)=j−(j^2 /2)+(j^3 /3)−(j^4 /4)+...+(((−1)^(n+1) j^n )/n)+... ∴ ln(dy/dx)=−x+ln{(lnx)lim_(h→0) (1/h)(1−1−h−(h^2 /(2!))−(h^3 /(3!))−...)+lim_(h→0) (1/h)((h/x)−(h^2 /(2x^2 ))+(h^3 /(3x^3 ))−...)} ln(dy/dx)=−x+ln{(lnx)lim_(h→0) (−1−(h/(2!))−(h^2 /(3!))−...)+lim_(h→0) ((1/x)−(h/(2x^2 ))+(h^2 /(3x^3 ))−...)} ln(dy/dx)=−x+ln{(lnx)(−1)+(1/x)} (dy/dx)=exp(−x+ln(x^(−1) −lnx))=e^(−x) ×(x^(−1) −lnx)

$${Let}\:{y}=\frac{{lnx}}{{e}^{{x}} }.\:{From}\:{first}\:{principles} \\ $$$$\frac{{dy}}{{dx}}=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{f}\left({x}+{h}\right)−{f}\left({x}\right)}{{h}} \\ $$$$=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{−{x}−{h}} {ln}\left({x}+{h}\right)−{e}^{−{x}} {lnx}}{{h}} \\ $$$$=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{{ln}\left({x}+{h}\right)}{{he}^{{x}+{h}} }−\frac{{lnx}}{{he}^{{x}} }\right) \\ $$$$=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{ln}\left({x}+{h}\right)−{e}^{{h}} {lnx}}{{he}^{{x}} {e}^{{h}} } \\ $$$$={e}^{−{x}} \underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{he}^{{h}} }\left({ln}\left({x}+{h}\right)−{lnx}^{{e}^{{h}} } \right) \\ $$$$={e}^{−{x}} \underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{he}^{{h}} }{ln}\frac{{x}+{h}}{{x}^{{e}^{{h}} } } \\ $$$$\frac{{dy}}{{dx}}={e}^{−{x}} \underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}{ln}\left({x}^{\mathrm{1}−{e}^{{h}} } +\frac{{h}}{{x}^{{e}^{{h}} } }\right)^{\mathrm{1}/{he}^{{h}} } \\ $$$${ln}\frac{{dy}}{{dx}}={ln}\left\{{e}^{−{x}} \right\}+{ln}\left(\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\frac{\mathrm{1}}{{e}^{{h}} }{ln}\left[\left({x}^{\mathrm{1}−{e}^{{h}} } +\frac{{h}}{{x}^{{e}^{{h}} } }\right)^{\mathrm{1}/{h}} \right]\right\}\right) \\ $$$${ln}\frac{{dy}}{{dx}}=−{x}+{ln}\left(\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{h}}{lnx}^{\mathrm{1}−{e}^{{h}} } \left(\mathrm{1}+\frac{{h}}{{x}}\right)\right) \\ $$$${ln}\frac{{dy}}{{dx}}=−{x}+{ln}\left(\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}−{e}^{{h}} }{{h}}{lnx}+\frac{\mathrm{1}}{{h}}{ln}\left(\mathrm{1}+\frac{{h}}{{x}}\right)\right)\right) \\ $$$$ \\ $$$$\bullet\:{e}\:{is}\:{a}\:{number}\:{such}\:{that}\:{for}\:{u}\:{being} \\ $$$${any}\:{number},\:{e}^{{u}} =\mathrm{1}+{u}+\frac{{u}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{u}^{\mathrm{3}} }{\mathrm{3}!}+...+\frac{{u}^{{n}} }{{n}!}+... \\ $$$$\bullet\:{For}\:{j}\in\left(−\mathrm{1},\mathrm{1}\right]\:{one}\:{can}\:{write} \\ $$$${ln}\left(\mathrm{1}+{j}\right)={j}−\frac{{j}^{\mathrm{2}} }{\mathrm{2}}+\frac{{j}^{\mathrm{3}} }{\mathrm{3}}−\frac{{j}^{\mathrm{4}} }{\mathrm{4}}+...+\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {j}^{{n}} }{{n}}+... \\ $$$$ \\ $$$$\therefore\:{ln}\frac{{dy}}{{dx}}=−{x}+{ln}\left\{\left({lnx}\right)\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{h}}\left(\mathrm{1}−\mathrm{1}−{h}−\frac{{h}^{\mathrm{2}} }{\mathrm{2}!}−\frac{{h}^{\mathrm{3}} }{\mathrm{3}!}−...\right)+\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{h}}\left(\frac{{h}}{{x}}−\frac{{h}^{\mathrm{2}} }{\mathrm{2}{x}^{\mathrm{2}} }+\frac{{h}^{\mathrm{3}} }{\mathrm{3}{x}^{\mathrm{3}} }−...\right)\right\} \\ $$$${ln}\frac{{dy}}{{dx}}=−{x}+{ln}\left\{\left({lnx}\right)\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(−\mathrm{1}−\frac{{h}}{\mathrm{2}!}−\frac{{h}^{\mathrm{2}} }{\mathrm{3}!}−...\right)+\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{{x}}−\frac{{h}}{\mathrm{2}{x}^{\mathrm{2}} }+\frac{{h}^{\mathrm{2}} }{\mathrm{3}{x}^{\mathrm{3}} }−...\right)\right\} \\ $$$${ln}\frac{{dy}}{{dx}}=−{x}+{ln}\left\{\left({lnx}\right)\left(−\mathrm{1}\right)+\frac{\mathrm{1}}{{x}}\right\} \\ $$$$\frac{{dy}}{{dx}}={exp}\left(−{x}+{ln}\left({x}^{−\mathrm{1}} −{lnx}\right)\right)={e}^{−{x}} ×\left({x}^{−\mathrm{1}} −{lnx}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by sanusihammed last updated on 24/May/16

This is great . wow.

$${This}\:{is}\:{great}\:.\:{wow}. \\ $$

Commented by sanusihammed last updated on 24/May/16

Thanks so much.

$${Thanks}\:{so}\:{much}. \\ $$

Commented by Yozzii last updated on 23/May/16

Alternatively, one could prove the quotient rule from first principles and subsequently apply it. Let r(x)=((u(x))/(v(x))) where u and v are functions of x and v(x)≠0. ∴ r(x+h)=((u(x+h))/(v(x+h))) (h=δx) ∴r(x+h)−r(x)=((u(x+h))/(v(x+h)))−((u(x))/(v(x)))=δr(x) =((v(x)(u(x+h)−u(x)+u(x))−u(x)(v(x+h)−v(x)+v(x)))/(v(x+h)v(x))) δr(x)=((v(x)δu(x)+v(x)u(x)−u(x)δv(x)−u(x)v(x))/(v(x+h)v(x))) δr(x)=((v(x)δu(x)−u(x)δv(x))/(v(x+δx)v(x))) By definition of the derivative, (dr/dx)=lim_(δx→0) ((δr(x))/(δx))=lim_(δx→0) (1/(δx))(((v(x)δu(x)−u(x)δv(x))/(v(x+δx)v(x)))) (dr/dx)=lim_(δx→0) ((v(x)((δu(x))/(δx))−u(x)((δv(x))/(δx)))/(v(x+δx)v(x))) Since v(x)≠0 for all x∈R, by the algebra of limits, ⇒(dr/dx)=((lim_(δx→0) (v(x)((δu(x))/(δx))−u(x)((δv(x))/(δx))))/(lim_(δx→0) {v(x+δx)v(x)})) (dr/dx)=((v(x)(lim_(δx→0) ((δu(x))/(δx)))−u(x)(lim_(δx→0) ((δv(x))/(δx))))/(lim_(δx→0) {v(x+δx)v(x)})) Now, we substitute the following results: lim_(δx→0) ((δu(x))/(δx))=(du/dx), lim_(δx→0) ((δv(x))/(δx))=(dv/dx) & lim_(δx→0) {v(x+δx)v(x)}=v(x+0)v(x)=v^2 (x). ∴(dr/dx)=((v(x)(du/dx)−u(x)(dv/dx))/(v^2 (x))) □ So, if r(x)=((lnx)/e^x ) ⇒(dr/dx)=((e^x x^(−1) −e^x lnx)/e^(2x) )=((x^(−1) −lnx)/e^x ).

$${Alternatively},\:{one}\:{could}\:{prove}\:{the} \\ $$$${quotient}\:{rule}\:{from}\:{first}\:{principles} \\ $$$${and}\:{subsequently}\:{apply}\:{it}.\: \\ $$$$ \\ $$$${Let}\:{r}\left({x}\right)=\frac{{u}\left({x}\right)}{{v}\left({x}\right)}\:{where}\:{u}\:{and}\:{v}\:{are}\:{functions} \\ $$$${of}\:{x}\:{and}\:{v}\left({x}\right)\neq\mathrm{0}. \\ $$$$\therefore\:{r}\left({x}+{h}\right)=\frac{{u}\left({x}+{h}\right)}{{v}\left({x}+{h}\right)}\:\:\:\:\:\left({h}=\delta{x}\right) \\ $$$$\therefore{r}\left({x}+{h}\right)−{r}\left({x}\right)=\frac{{u}\left({x}+{h}\right)}{{v}\left({x}+{h}\right)}−\frac{{u}\left({x}\right)}{{v}\left({x}\right)}=\delta{r}\left({x}\right) \\ $$$$=\frac{{v}\left({x}\right)\left({u}\left({x}+{h}\right)−{u}\left({x}\right)+{u}\left({x}\right)\right)−{u}\left({x}\right)\left({v}\left({x}+{h}\right)−{v}\left({x}\right)+{v}\left({x}\right)\right)}{{v}\left({x}+{h}\right){v}\left({x}\right)} \\ $$$$\delta{r}\left({x}\right)=\frac{{v}\left({x}\right)\delta{u}\left({x}\right)+{v}\left({x}\right){u}\left({x}\right)−{u}\left({x}\right)\delta{v}\left({x}\right)−{u}\left({x}\right){v}\left({x}\right)}{{v}\left({x}+{h}\right){v}\left({x}\right)} \\ $$$$\delta{r}\left({x}\right)=\frac{{v}\left({x}\right)\delta{u}\left({x}\right)−{u}\left({x}\right)\delta{v}\left({x}\right)}{{v}\left({x}+\delta{x}\right){v}\left({x}\right)} \\ $$$${By}\:{definition}\:{of}\:{the}\:{derivative}, \\ $$$$\frac{{dr}}{{dx}}=\underset{\delta{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\delta{r}\left({x}\right)}{\delta{x}}=\underset{\delta{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{\delta{x}}\left(\frac{{v}\left({x}\right)\delta{u}\left({x}\right)−{u}\left({x}\right)\delta{v}\left({x}\right)}{{v}\left({x}+\delta{x}\right){v}\left({x}\right)}\right) \\ $$$$\frac{{dr}}{{dx}}=\underset{\delta{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{v}\left({x}\right)\frac{\delta{u}\left({x}\right)}{\delta{x}}−{u}\left({x}\right)\frac{\delta{v}\left({x}\right)}{\delta{x}}}{{v}\left({x}+\delta{x}\right){v}\left({x}\right)} \\ $$$${Since}\:{v}\left({x}\right)\neq\mathrm{0}\:{for}\:{all}\:{x}\in\mathbb{R},\:{by}\:{the}\:{algebra} \\ $$$${of}\:{limits}, \\ $$$$\Rightarrow\frac{{dr}}{{dx}}=\frac{\underset{\delta{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left({v}\left({x}\right)\frac{\delta{u}\left({x}\right)}{\delta{x}}−{u}\left({x}\right)\frac{\delta{v}\left({x}\right)}{\delta{x}}\right)}{\underset{\delta{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{{v}\left({x}+\delta{x}\right){v}\left({x}\right)\right\}} \\ $$$$\frac{{dr}}{{dx}}=\frac{{v}\left({x}\right)\left(\underset{\delta{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\delta{u}\left({x}\right)}{\delta{x}}\right)−{u}\left({x}\right)\left(\underset{\delta{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\delta{v}\left({x}\right)}{\delta{x}}\right)}{\underset{\delta{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{{v}\left({x}+\delta{x}\right){v}\left({x}\right)\right\}} \\ $$$${Now},\:{we}\:{substitute}\:{the}\:{following}\:{results}: \\ $$$$\underset{\delta{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\delta{u}\left({x}\right)}{\delta{x}}=\frac{{du}}{{dx}},\:\underset{\delta{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\delta{v}\left({x}\right)}{\delta{x}}=\frac{{dv}}{{dx}}\:\:\:\&\: \\ $$$$\underset{\delta{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{{v}\left({x}+\delta{x}\right){v}\left({x}\right)\right\}={v}\left({x}+\mathrm{0}\right){v}\left({x}\right)={v}^{\mathrm{2}} \left({x}\right). \\ $$$$\therefore\frac{{dr}}{{dx}}=\frac{{v}\left({x}\right)\frac{{du}}{{dx}}−{u}\left({x}\right)\frac{{dv}}{{dx}}}{{v}^{\mathrm{2}} \left({x}\right)}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Box \\ $$$$ \\ $$$${So},\:{if}\:{r}\left({x}\right)=\frac{{lnx}}{{e}^{{x}} } \\ $$$$\Rightarrow\frac{{dr}}{{dx}}=\frac{{e}^{{x}} {x}^{−\mathrm{1}} −{e}^{{x}} {lnx}}{{e}^{\mathrm{2}{x}} }=\frac{{x}^{−\mathrm{1}} −{lnx}}{{e}^{{x}} }. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com