Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 5673 by sanusihammed last updated on 23/May/16

Using inductive method. prove that .. 7^(2n) + 16n − 1 is divisible by 4 please help.

$${Using}\:{inductive}\:{method}.\:{prove}\:{that}\:.. \\ $$$$ \\ $$$$\mathrm{7}^{\mathrm{2}{n}} \:+\:\mathrm{16}{n}\:−\:\mathrm{1}\:{is}\:{divisible}\:{by}\:\mathrm{4} \\ $$$$ \\ $$$${please}\:{help}. \\ $$

Commented by Rasheed Soomro last updated on 24/May/16

I think 16n is dropable at start. it is unnecessary. Because 4 ∣ 16n so it is sufficient to prove “7^(2n) −1 is divisible by 4” •7^(2(1)) −1=48 which is divisible by4 •Let 4 ∣ 7^(2k) −1 So 7^(2k) −1=4m where m∈Z 7^(2k) =4m+1 7^(2k) .7^2 =7^2 (4m+1)=196m+49 7^(2(k+1)) −1=196m+48=4(49m+12) So 4 ∣ 7^(2(k+1)) −1 if 4 ∣ 7^(2k) −1 And hence for any n∈N, 4 ∣ 7^(2n) −1 since 4 ∣ 16n So finally, 4 ∣ 7^(2n) +16n−1 for any n∈N

$$\mathrm{I}\:\mathrm{think}\:\mathrm{16n}\:\mathrm{is}\:\mathrm{dropable}\:\mathrm{at}\:\mathrm{start}. \\ $$$$\mathrm{it}\:\mathrm{is}\:\mathrm{unnecessary}. \\ $$$$\mathrm{Because}\:\:\mathrm{4}\:\mid\:\mathrm{16n}\:\mathrm{so}\:\mathrm{it}\:\mathrm{is}\:\mathrm{sufficient}\:\mathrm{to}\:\mathrm{prove} \\ $$$$``\mathrm{7}^{\mathrm{2n}} −\mathrm{1}\:\mathrm{is}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{4}'' \\ $$$$\bullet\mathrm{7}^{\mathrm{2}\left(\mathrm{1}\right)} −\mathrm{1}=\mathrm{48}\:\mathrm{which}\:\mathrm{is}\:\mathrm{divisible}\:\mathrm{by4} \\ $$$$\bullet\mathrm{Let}\:\mathrm{4}\:\mid\:\mathrm{7}^{\mathrm{2k}} −\mathrm{1}\: \\ $$$$\mathrm{So}\:\:\:\mathrm{7}^{\mathrm{2k}} −\mathrm{1}=\mathrm{4m}\:\mathrm{where}\:\mathrm{m}\in\mathbb{Z} \\ $$$$\mathrm{7}^{\mathrm{2k}} =\mathrm{4m}+\mathrm{1} \\ $$$$\mathrm{7}^{\mathrm{2k}} .\mathrm{7}^{\mathrm{2}} =\mathrm{7}^{\mathrm{2}} \left(\mathrm{4m}+\mathrm{1}\right)=\mathrm{196m}+\mathrm{49} \\ $$$$\mathrm{7}^{\mathrm{2}\left(\mathrm{k}+\mathrm{1}\right)} −\mathrm{1}=\mathrm{196m}+\mathrm{48}=\mathrm{4}\left(\mathrm{49m}+\mathrm{12}\right) \\ $$$$\mathrm{So}\:\:\mathrm{4}\:\mid\:\mathrm{7}^{\mathrm{2}\left(\mathrm{k}+\mathrm{1}\right)} −\mathrm{1}\:\mathrm{if}\:\mathrm{4}\:\mid\:\mathrm{7}^{\mathrm{2k}} −\mathrm{1} \\ $$$$\mathrm{And}\:\mathrm{hence} \\ $$$$\mathrm{for}\:\mathrm{any}\:\mathrm{n}\in\mathbb{N},\:\mathrm{4}\:\mid\:\mathrm{7}^{\mathrm{2n}} −\mathrm{1} \\ $$$$\mathrm{since}\:\mathrm{4}\:\mid\:\mathrm{16n} \\ $$$$\mathrm{So}\:\mathrm{finally}, \\ $$$$\:\:\:\:\:\:\mathrm{4}\:\mid\:\mathrm{7}^{\mathrm{2n}} +\mathrm{16n}−\mathrm{1}\:\mathrm{for}\:\mathrm{any}\:\mathrm{n}\in\mathbb{N} \\ $$

Answered by Yozzii last updated on 24/May/16

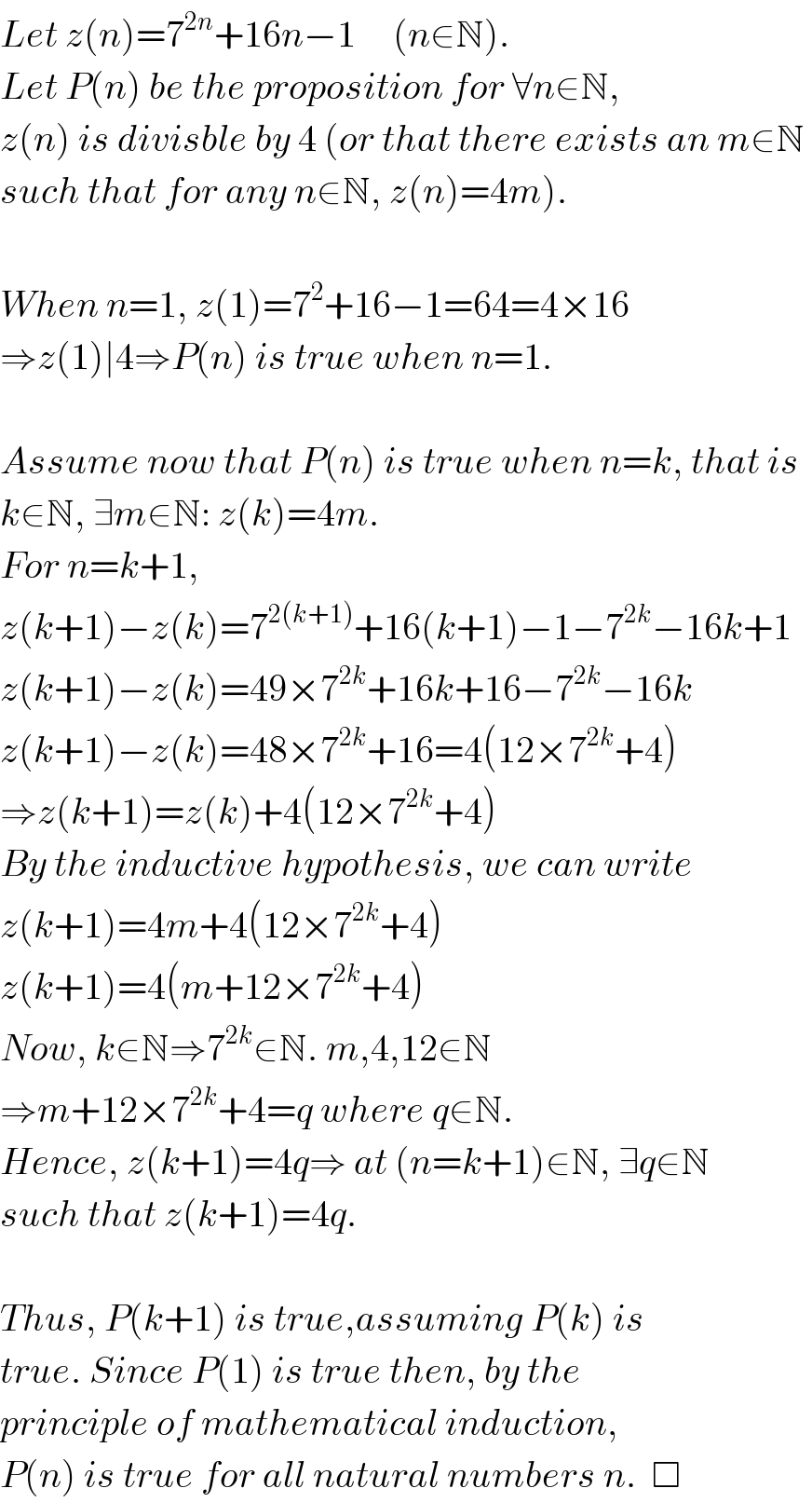
Let z(n)=7^(2n) +16n−1 (n∈N). Let P(n) be the proposition for ∀n∈N, z(n) is divisble by 4 (or that there exists an m∈N such that for any n∈N, z(n)=4m). When n=1, z(1)=7^2 +16−1=64=4×16 ⇒z(1)∣4⇒P(n) is true when n=1. Assume now that P(n) is true when n=k, that is k∈N, ∃m∈N: z(k)=4m. For n=k+1, z(k+1)−z(k)=7^(2(k+1)) +16(k+1)−1−7^(2k) −16k+1 z(k+1)−z(k)=49×7^(2k) +16k+16−7^(2k) −16k z(k+1)−z(k)=48×7^(2k) +16=4(12×7^(2k) +4) ⇒z(k+1)=z(k)+4(12×7^(2k) +4) By the inductive hypothesis, we can write z(k+1)=4m+4(12×7^(2k) +4) z(k+1)=4(m+12×7^(2k) +4) Now, k∈N⇒7^(2k) ∈N. m,4,12∈N ⇒m+12×7^(2k) +4=q where q∈N. Hence, z(k+1)=4q⇒ at (n=k+1)∈N, ∃q∈N such that z(k+1)=4q. Thus, P(k+1) is true,assuming P(k) is true. Since P(1) is true then, by the principle of mathematical induction, P(n) is true for all natural numbers n. □

$${Let}\:{z}\left({n}\right)=\mathrm{7}^{\mathrm{2}{n}} +\mathrm{16}{n}−\mathrm{1}\:\:\:\:\:\left({n}\in\mathbb{N}\right). \\ $$$${Let}\:{P}\left({n}\right)\:{be}\:{the}\:{proposition}\:{for}\:\forall{n}\in\mathbb{N}, \\ $$$${z}\left({n}\right)\:{is}\:{divisble}\:{by}\:\mathrm{4}\:\left({or}\:{that}\:{there}\:{exists}\:{an}\:{m}\in\mathbb{N}\:\right. \\ $$$$\left.{such}\:{that}\:{for}\:{any}\:{n}\in\mathbb{N},\:{z}\left({n}\right)=\mathrm{4}{m}\right). \\ $$$$ \\ $$$${When}\:{n}=\mathrm{1},\:{z}\left(\mathrm{1}\right)=\mathrm{7}^{\mathrm{2}} +\mathrm{16}−\mathrm{1}=\mathrm{64}=\mathrm{4}×\mathrm{16} \\ $$$$\Rightarrow{z}\left(\mathrm{1}\right)\mid\mathrm{4}\Rightarrow{P}\left({n}\right)\:{is}\:{true}\:{when}\:{n}=\mathrm{1}. \\ $$$$ \\ $$$${Assume}\:{now}\:{that}\:{P}\left({n}\right)\:{is}\:{true}\:{when}\:{n}={k},\:{that}\:{is} \\ $$$${k}\in\mathbb{N},\:\exists{m}\in\mathbb{N}:\:{z}\left({k}\right)=\mathrm{4}{m}. \\ $$$${For}\:{n}={k}+\mathrm{1}, \\ $$$${z}\left({k}+\mathrm{1}\right)−{z}\left({k}\right)=\mathrm{7}^{\mathrm{2}\left({k}+\mathrm{1}\right)} +\mathrm{16}\left({k}+\mathrm{1}\right)−\mathrm{1}−\mathrm{7}^{\mathrm{2}{k}} −\mathrm{16}{k}+\mathrm{1} \\ $$$${z}\left({k}+\mathrm{1}\right)−{z}\left({k}\right)=\mathrm{49}×\mathrm{7}^{\mathrm{2}{k}} +\mathrm{16}{k}+\mathrm{16}−\mathrm{7}^{\mathrm{2}{k}} −\mathrm{16}{k} \\ $$$${z}\left({k}+\mathrm{1}\right)−{z}\left({k}\right)=\mathrm{48}×\mathrm{7}^{\mathrm{2}{k}} +\mathrm{16}=\mathrm{4}\left(\mathrm{12}×\mathrm{7}^{\mathrm{2}{k}} +\mathrm{4}\right) \\ $$$$\Rightarrow{z}\left({k}+\mathrm{1}\right)={z}\left({k}\right)+\mathrm{4}\left(\mathrm{12}×\mathrm{7}^{\mathrm{2}{k}} +\mathrm{4}\right) \\ $$$${By}\:{the}\:{inductive}\:{hypothesis},\:{we}\:{can}\:{write} \\ $$$${z}\left({k}+\mathrm{1}\right)=\mathrm{4}{m}+\mathrm{4}\left(\mathrm{12}×\mathrm{7}^{\mathrm{2}{k}} +\mathrm{4}\right) \\ $$$${z}\left({k}+\mathrm{1}\right)=\mathrm{4}\left({m}+\mathrm{12}×\mathrm{7}^{\mathrm{2}{k}} +\mathrm{4}\right) \\ $$$${Now},\:{k}\in\mathbb{N}\Rightarrow\mathrm{7}^{\mathrm{2}{k}} \in\mathbb{N}.\:{m},\mathrm{4},\mathrm{12}\in\mathbb{N} \\ $$$$\Rightarrow{m}+\mathrm{12}×\mathrm{7}^{\mathrm{2}{k}} +\mathrm{4}={q}\:{where}\:{q}\in\mathbb{N}. \\ $$$${Hence},\:{z}\left({k}+\mathrm{1}\right)=\mathrm{4}{q}\Rightarrow\:{at}\:\left({n}={k}+\mathrm{1}\right)\in\mathbb{N},\:\exists{q}\in\mathbb{N} \\ $$$${such}\:{that}\:{z}\left({k}+\mathrm{1}\right)=\mathrm{4}{q}. \\ $$$$ \\ $$$${Thus},\:{P}\left({k}+\mathrm{1}\right)\:{is}\:{true},{assuming}\:{P}\left({k}\right)\:{is} \\ $$$${true}.\:{Since}\:{P}\left(\mathrm{1}\right)\:{is}\:{true}\:{then},\:{by}\:{the} \\ $$$${principle}\:{of}\:{mathematical}\:{induction}, \\ $$$${P}\left({n}\right)\:{is}\:{true}\:{for}\:{all}\:{natural}\:{numbers}\:{n}.\:\:\Box \\ $$

Commented by sanusihammed last updated on 24/May/16

I really appreciate this . thank you.

$${I}\:{really}\:{appreciate}\:{this}\:.\:{thank}\:{you}. \\ $$

Answered by prakash jain last updated on 23/May/16

n=1 7^2 +16−1=49+16−1=64 64 is divisible by 4 so statment 7^(2n) +16n−1 is divisible by 4 is true for n=1. Assume that the statement is true for n=k i.e. 7^(2k) +16k−1 is divible by 4. or 7^(2k) +16k−1=4m 7^(2(k+1)) +16(k+1)−1 =7^(2k) 7^2 +16k+16−1 =7^(2k) ∙49+16k+15 =7^(2k) ∙49+16k∙49−16k∙48−49+49+15 =49(7^(2k) +16k−1)−48∙16k+64 =49(4m)−4∙12∙16k+4∙16 =4(49m−12∙16k+16) 49m−12∙16k+16 is an integer so if 7^(2k) +16k−1 is divible by 4 ⇒ 7^(2(k+1)) +16(k+1)−1 is divisble by 4.

$${n}=\mathrm{1} \\ $$$$\mathrm{7}^{\mathrm{2}} +\mathrm{16}−\mathrm{1}=\mathrm{49}+\mathrm{16}−\mathrm{1}=\mathrm{64} \\ $$$$\mathrm{64}\:\mathrm{is}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{4}\:\mathrm{so}\:\mathrm{statment}\:\mathrm{7}^{\mathrm{2}{n}} +\mathrm{16}{n}−\mathrm{1}\:\mathrm{is} \\ $$$$\mathrm{divisible}\:\mathrm{by}\:\mathrm{4}\:\mathrm{is}\:\mathrm{true}\:\mathrm{for}\:\mathrm{n}=\mathrm{1}. \\ $$$$\mathrm{Assume}\:\mathrm{that}\:\mathrm{the}\:\mathrm{statement}\:\mathrm{is}\:\mathrm{true}\:\mathrm{for}\:{n}={k} \\ $$$$\mathrm{i}.\mathrm{e}.\:\mathrm{7}^{\mathrm{2}{k}} +\mathrm{16}{k}−\mathrm{1}\:\mathrm{is}\:\mathrm{divible}\:\mathrm{by}\:\mathrm{4}. \\ $$$$\mathrm{or}\:\mathrm{7}^{\mathrm{2}{k}} +\mathrm{16}{k}−\mathrm{1}=\mathrm{4}{m} \\ $$$$\mathrm{7}^{\mathrm{2}\left({k}+\mathrm{1}\right)} +\mathrm{16}\left({k}+\mathrm{1}\right)−\mathrm{1} \\ $$$$=\mathrm{7}^{\mathrm{2}{k}} \mathrm{7}^{\mathrm{2}} +\mathrm{16}{k}+\mathrm{16}−\mathrm{1} \\ $$$$=\mathrm{7}^{\mathrm{2}{k}} \centerdot\mathrm{49}+\mathrm{16}{k}+\mathrm{15} \\ $$$$=\mathrm{7}^{\mathrm{2}{k}} \centerdot\mathrm{49}+\mathrm{16}{k}\centerdot\mathrm{49}−\mathrm{16}{k}\centerdot\mathrm{48}−\mathrm{49}+\mathrm{49}+\mathrm{15} \\ $$$$=\mathrm{49}\left(\mathrm{7}^{\mathrm{2}{k}} +\mathrm{16}{k}−\mathrm{1}\right)−\mathrm{48}\centerdot\mathrm{16}{k}+\mathrm{64} \\ $$$$=\mathrm{49}\left(\mathrm{4}{m}\right)−\mathrm{4}\centerdot\mathrm{12}\centerdot\mathrm{16}{k}+\mathrm{4}\centerdot\mathrm{16} \\ $$$$=\mathrm{4}\left(\mathrm{49}{m}−\mathrm{12}\centerdot\mathrm{16}{k}+\mathrm{16}\right) \\ $$$$\mathrm{49}{m}−\mathrm{12}\centerdot\mathrm{16}{k}+\mathrm{16}\:\mathrm{is}\:\mathrm{an}\:\mathrm{integer}\:\mathrm{so} \\ $$$$\mathrm{if}\:\:\mathrm{7}^{\mathrm{2}{k}} +\mathrm{16}{k}−\mathrm{1}\:\mathrm{is}\:\mathrm{divible}\:\mathrm{by}\:\mathrm{4}\:\Rightarrow \\ $$$$\mathrm{7}^{\mathrm{2}\left({k}+\mathrm{1}\right)} +\mathrm{16}\left({k}+\mathrm{1}\right)−\mathrm{1}\:\mathrm{is}\:\mathrm{divisble}\:\mathrm{by}\:\mathrm{4}. \\ $$

Commented by sanusihammed last updated on 24/May/16

Thanks for taking you time. i appreciate. thanks

$${Thanks}\:{for}\:{taking}\:{you}\:{time}.\:{i}\:{appreciate}.\:{thanks} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com