Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 56864 by Joel578 last updated on 25/Mar/19

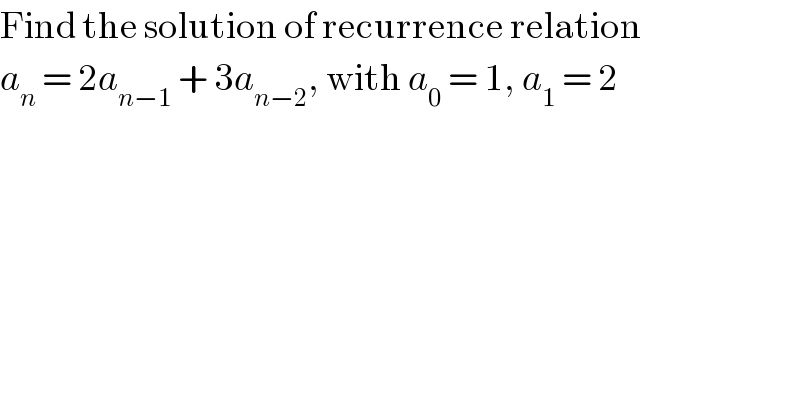
Find the solution of recurrence relation a_n = 2a_(n−1) + 3a_(n−2) , with a_0 = 1, a_1 = 2

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{of}\:\mathrm{recurrence}\:\mathrm{relation} \\ $$$${a}_{{n}} \:=\:\mathrm{2}{a}_{{n}−\mathrm{1}} \:+\:\mathrm{3}{a}_{{n}−\mathrm{2}} ,\:\mathrm{with}\:{a}_{\mathrm{0}} \:=\:\mathrm{1},\:{a}_{\mathrm{1}} \:=\:\mathrm{2} \\ $$

Commented by maxmathsup by imad last updated on 25/Mar/19

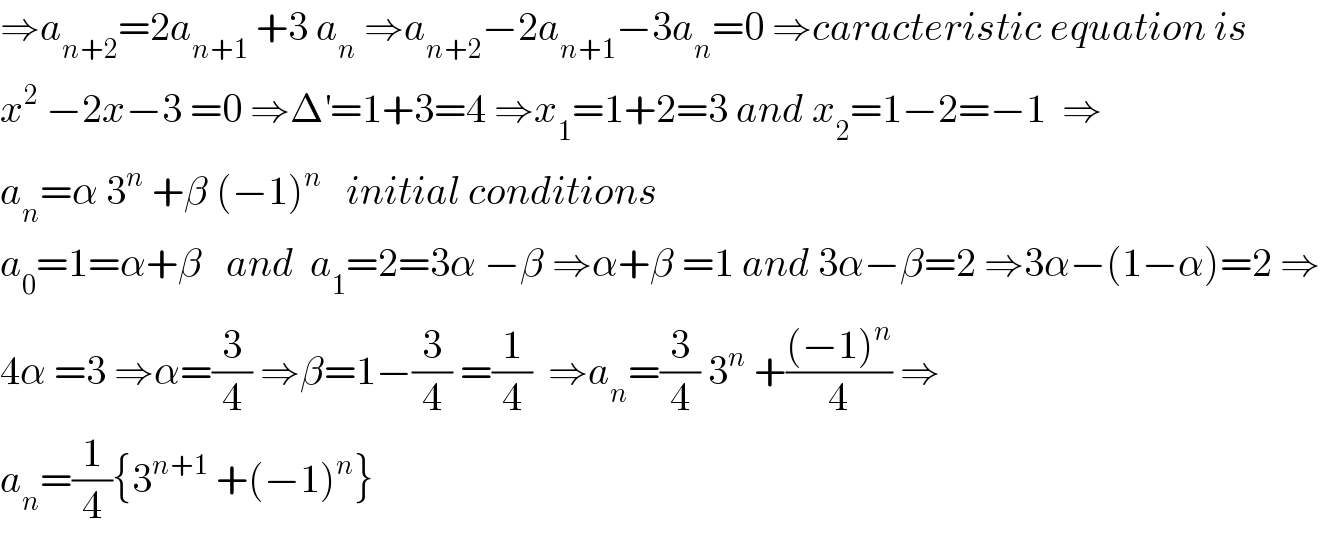
⇒a_(n+2) =2a_(n+1) +3 a_n ⇒a_(n+2) −2a_(n+1) −3a_n =0 ⇒caracteristic equation is x^2 −2x−3 =0 ⇒Δ^′ =1+3=4 ⇒x_1 =1+2=3 and x_2 =1−2=−1 ⇒ a_n =α 3^n +β (−1)^n initial conditions a_0 =1=α+β and a_1 =2=3α −β ⇒α+β =1 and 3α−β=2 ⇒3α−(1−α)=2 ⇒ 4α =3 ⇒α=(3/4) ⇒β=1−(3/4) =(1/4) ⇒a_n =(3/4) 3^n +(((−1)^n )/4) ⇒ a_n =(1/4){3^(n+1) +(−1)^n }

$$\Rightarrow{a}_{{n}+\mathrm{2}} =\mathrm{2}{a}_{{n}+\mathrm{1}} \:+\mathrm{3}\:{a}_{{n}} \:\Rightarrow{a}_{{n}+\mathrm{2}} −\mathrm{2}{a}_{{n}+\mathrm{1}} −\mathrm{3}{a}_{{n}} =\mathrm{0}\:\Rightarrow{caracteristic}\:{equation}\:{is} \\ $$$${x}^{\mathrm{2}} \:−\mathrm{2}{x}−\mathrm{3}\:=\mathrm{0}\:\Rightarrow\Delta^{'} =\mathrm{1}+\mathrm{3}=\mathrm{4}\:\Rightarrow{x}_{\mathrm{1}} =\mathrm{1}+\mathrm{2}=\mathrm{3}\:{and}\:{x}_{\mathrm{2}} =\mathrm{1}−\mathrm{2}=−\mathrm{1}\:\:\Rightarrow \\ $$$${a}_{{n}} =\alpha\:\mathrm{3}^{{n}} \:+\beta\:\left(−\mathrm{1}\right)^{{n}} \:\:\:{initial}\:{conditions} \\ $$$${a}_{\mathrm{0}} =\mathrm{1}=\alpha+\beta\:\:\:{and}\:\:{a}_{\mathrm{1}} =\mathrm{2}=\mathrm{3}\alpha\:−\beta\:\Rightarrow\alpha+\beta\:=\mathrm{1}\:{and}\:\mathrm{3}\alpha−\beta=\mathrm{2}\:\Rightarrow\mathrm{3}\alpha−\left(\mathrm{1}−\alpha\right)=\mathrm{2}\:\Rightarrow \\ $$$$\mathrm{4}\alpha\:=\mathrm{3}\:\Rightarrow\alpha=\frac{\mathrm{3}}{\mathrm{4}}\:\Rightarrow\beta=\mathrm{1}−\frac{\mathrm{3}}{\mathrm{4}}\:=\frac{\mathrm{1}}{\mathrm{4}}\:\:\Rightarrow{a}_{{n}} =\frac{\mathrm{3}}{\mathrm{4}}\:\mathrm{3}^{{n}} \:+\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{4}}\:\Rightarrow \\ $$$${a}_{{n}} =\frac{\mathrm{1}}{\mathrm{4}}\left\{\mathrm{3}^{{n}+\mathrm{1}} \:+\left(−\mathrm{1}\right)^{{n}} \right\} \\ $$

Commented by Joel578 last updated on 26/Mar/19

thank you very much

$${thank}\:{you}\:{very}\:{much} \\ $$

Commented by turbo msup by abdo last updated on 26/Mar/19

you are welcome

$${you}\:{are}\:{welcome} \\ $$

Answered by mr W last updated on 25/Mar/19

let a_n =Ap^n +Bq^n ⇒ Ap^n +Bq^n =2Ap^(n−1) +2Bq^(n−1) +3Ap^(n−2) +3Bq^(n−2) ⇒ A(p^2 −2p−3)p^(n−2) +B(q^2 −2q−3)q^(n−2) =0 ⇒p and q are roots of x^2 −2x−3=0 (x+1)(x−3)=0 ⇒p=−1 and q=3 ⇒a_n =A×(−1)^n +B×3^n ⇒a_0 =A+B=1 ...(i) ⇒a_1 =−A+3B=2 ...(ii) ⇒A=(1/4) ⇒B=(3/4) ⇒a_n =(1/4)[(−1)^n +3^(n+1) ]

$${let}\:{a}_{{n}} ={Ap}^{{n}} +{Bq}^{{n}} \\ $$$$\Rightarrow\:{Ap}^{{n}} +{Bq}^{{n}} =\mathrm{2}{Ap}^{{n}−\mathrm{1}} +\mathrm{2}{Bq}^{{n}−\mathrm{1}} +\mathrm{3}{Ap}^{{n}−\mathrm{2}} +\mathrm{3}{Bq}^{{n}−\mathrm{2}} \\ $$$$\Rightarrow\:{A}\left({p}^{\mathrm{2}} −\mathrm{2}{p}−\mathrm{3}\right){p}^{{n}−\mathrm{2}} +{B}\left({q}^{\mathrm{2}} −\mathrm{2}{q}−\mathrm{3}\right){q}^{{n}−\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{p}\:{and}\:{q}\:{are}\:{roots}\:{of} \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{3}=\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)\left({x}−\mathrm{3}\right)=\mathrm{0} \\ $$$$\Rightarrow{p}=−\mathrm{1}\:{and}\:{q}=\mathrm{3} \\ $$$$\Rightarrow{a}_{{n}} ={A}×\left(−\mathrm{1}\right)^{{n}} +{B}×\mathrm{3}^{{n}} \\ $$$$\Rightarrow{a}_{\mathrm{0}} ={A}+{B}=\mathrm{1}\:\:\:...\left({i}\right) \\ $$$$\Rightarrow{a}_{\mathrm{1}} =−{A}+\mathrm{3}{B}=\mathrm{2}\:\:\:...\left({ii}\right) \\ $$$$\Rightarrow{A}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow{B}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow{a}_{{n}} =\frac{\mathrm{1}}{\mathrm{4}}\left[\left(−\mathrm{1}\right)^{{n}} +\mathrm{3}^{{n}+\mathrm{1}} \right] \\ $$

Commented by Joel578 last updated on 26/Mar/19

thank you very much

$${thank}\:{you}\:{very}\:{much} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com