
Question and Answers Forum
Question Number 56886 by gunawan last updated on 25/Mar/19
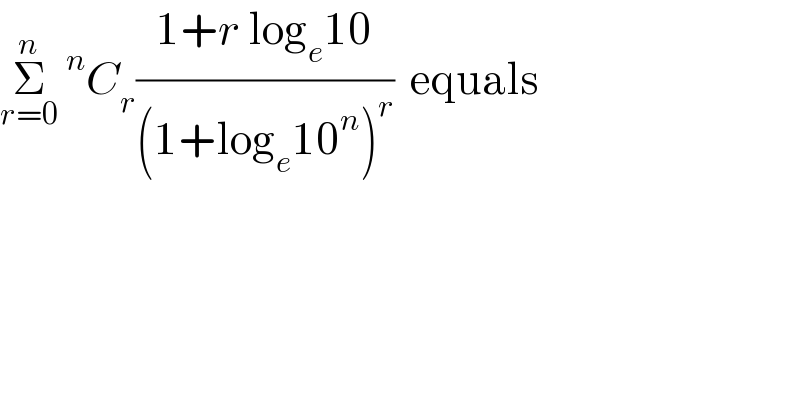
Answered by tanmay.chaudhury50@gmail.com last updated on 27/Mar/19
![a=log_e 10 and (1+nlog_e 10)=b [b=1+na] Σ_(r=0) ^n nC_r ×((1+ar)/((b)^r ))=Σ_(r=0) ^n nC_r ×(1/b^r )+aΣ_(r=0) ^n nC_r ×(r/b^r ) (1+(1/b))^n =nC_0 ×1^n +nC_1 ×(1/b^1 )+nC_2 ×(1/b^2 )+..+nC_n ×(1/b^n ) so Σ_(r=0) ^n nC_r ×(1/b^r )=(1+(1/b))^n ⇚look here aΣ_(r=0) ^n nC_r ×(r/b^r ) =a(nC_o ×(0/b^0 )+nC_1 ×(1/b^1 )+nC_2 ×(2/b^2 )+..+nC_n ×(n/b^n )) now (1+(x/b))^n =nC_0 ×(x^0 /b^0 )+nC_1 ×(x^1 /b^1 )+nC_2 ×(x^2 /b^2 )+..+nC_n ×(x^n /b^n ) differentiate both side w.r.t x n(1+(x/b))^(n−1) ×(1/b)=nC_0 ×0+nC_1 ×(1/b^1 )+nC_2 ×((2x)/b^2 )+...+nC_n ×((nx^(n−1) )/b^n ) now put x=1 both side n(1+(1/b))^(n−1) =Σ_(r=0) ^n nC_r ×(r/b^r ) so value of aΣ_(r=0) ^n nC_r ×(r/b^r )=a×n(1+(1/b))^(n−1) ⇚look here hence rewuired answer is Σ_(r=0) ^n nC_r ×(1/b^r )+aΣ_(r=0) ^n nC_n ×(r/b^r ) =(1+(1/b))^n +a×n(1+(1/b))^(n−1) =(1+(1/b))^(n−1) ×(1+(1/b)+an) [b=1+na and a=log_e 10] =(1+(1/(1+na)))^(n−1) ×(1+na+(1/(1+na))) =(1+(1/(nlog_e 10)))^(n−1) (1+nlog_e 10+(1/(1+nlog_e 10)))](Q56956.png)
| ||
Question and Answers Forum | ||
Question Number 56886 by gunawan last updated on 25/Mar/19 | ||
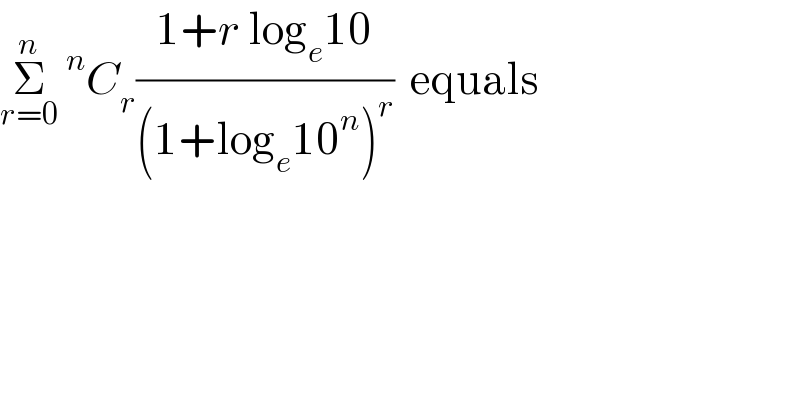 | ||
Answered by tanmay.chaudhury50@gmail.com last updated on 27/Mar/19 | ||
![a=log_e 10 and (1+nlog_e 10)=b [b=1+na] Σ_(r=0) ^n nC_r ×((1+ar)/((b)^r ))=Σ_(r=0) ^n nC_r ×(1/b^r )+aΣ_(r=0) ^n nC_r ×(r/b^r ) (1+(1/b))^n =nC_0 ×1^n +nC_1 ×(1/b^1 )+nC_2 ×(1/b^2 )+..+nC_n ×(1/b^n ) so Σ_(r=0) ^n nC_r ×(1/b^r )=(1+(1/b))^n ⇚look here aΣ_(r=0) ^n nC_r ×(r/b^r ) =a(nC_o ×(0/b^0 )+nC_1 ×(1/b^1 )+nC_2 ×(2/b^2 )+..+nC_n ×(n/b^n )) now (1+(x/b))^n =nC_0 ×(x^0 /b^0 )+nC_1 ×(x^1 /b^1 )+nC_2 ×(x^2 /b^2 )+..+nC_n ×(x^n /b^n ) differentiate both side w.r.t x n(1+(x/b))^(n−1) ×(1/b)=nC_0 ×0+nC_1 ×(1/b^1 )+nC_2 ×((2x)/b^2 )+...+nC_n ×((nx^(n−1) )/b^n ) now put x=1 both side n(1+(1/b))^(n−1) =Σ_(r=0) ^n nC_r ×(r/b^r ) so value of aΣ_(r=0) ^n nC_r ×(r/b^r )=a×n(1+(1/b))^(n−1) ⇚look here hence rewuired answer is Σ_(r=0) ^n nC_r ×(1/b^r )+aΣ_(r=0) ^n nC_n ×(r/b^r ) =(1+(1/b))^n +a×n(1+(1/b))^(n−1) =(1+(1/b))^(n−1) ×(1+(1/b)+an) [b=1+na and a=log_e 10] =(1+(1/(1+na)))^(n−1) ×(1+na+(1/(1+na))) =(1+(1/(nlog_e 10)))^(n−1) (1+nlog_e 10+(1/(1+nlog_e 10)))](Q56956.png) | ||
| ||