Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 5692 by FilupSmith last updated on 24/May/16

f(x)=e^x g(x)=ln x h(x)=x A line L is perpendicular to h(x) at point P(x,y) and extends and disects f(x) and g(x). The length of L between f(x) and g(x) is r. When is r minimum?

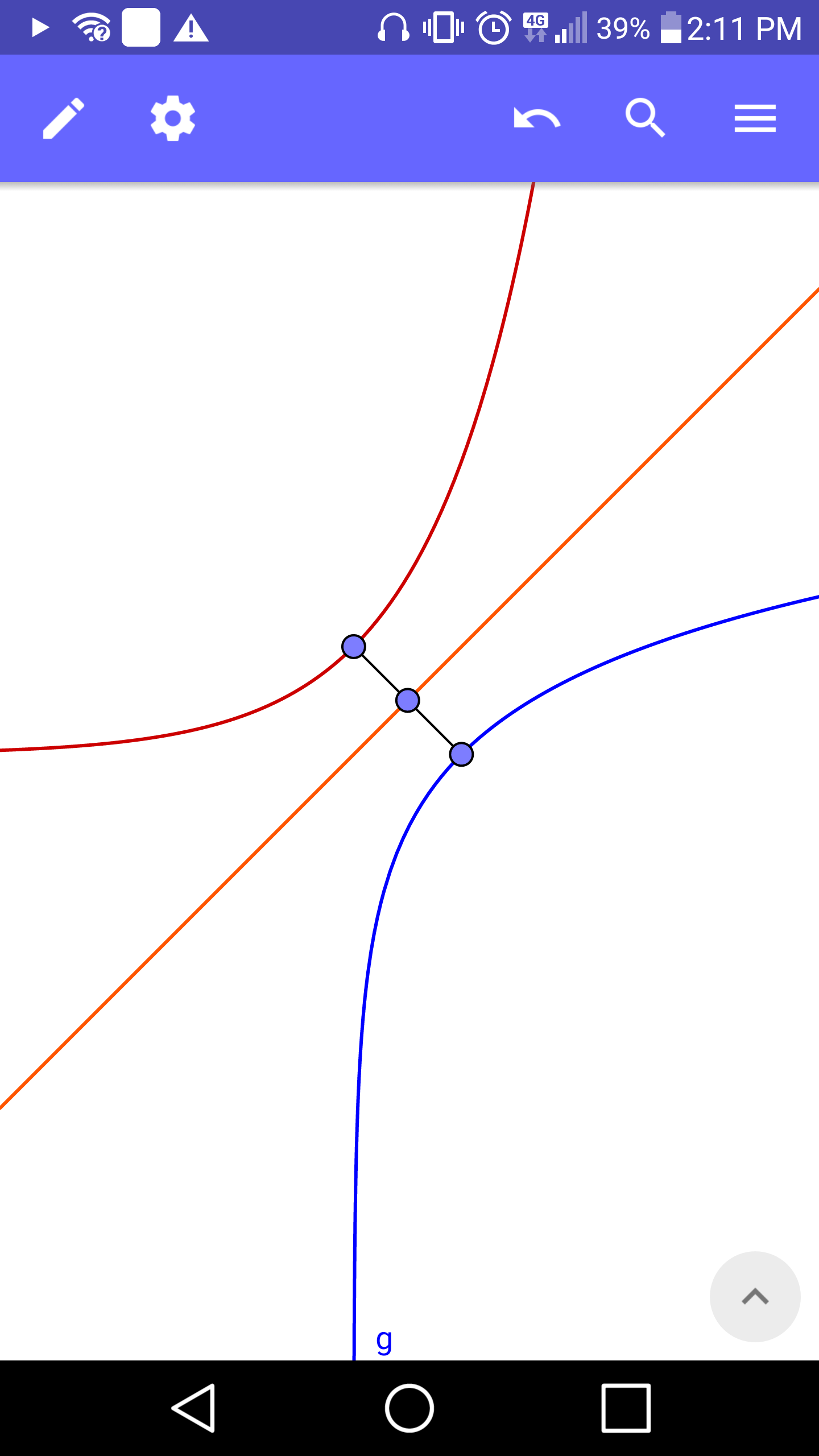
$${f}\left({x}\right)={e}^{{x}} \\ $$$${g}\left({x}\right)=\mathrm{ln}\:{x} \\ $$$${h}\left({x}\right)={x} \\ $$$$ \\ $$$$\mathrm{A}\:\mathrm{line}\:{L}\:\mathrm{is}\:\mathrm{perpendicular}\:\mathrm{to}\:{h}\left({x}\right)\:\mathrm{at}\:\mathrm{point} \\ $$$${P}\left({x},{y}\right)\:\mathrm{and}\:\mathrm{extends}\:\mathrm{and}\:\mathrm{disects}\:{f}\left({x}\right)\:\mathrm{and}\:{g}\left({x}\right). \\ $$$$\mathrm{The}\:\mathrm{length}\:\mathrm{of}\:{L}\:\mathrm{between}\:{f}\left({x}\right)\:{and}\:{g}\left({x}\right) \\ $$$$\mathrm{is}\:{r}.\:\mathrm{When}\:\mathrm{is}\:{r}\:\mathrm{minimum}? \\ $$

Commented by FilupSmith last updated on 24/May/16

Commented by Yozzii last updated on 25/May/16

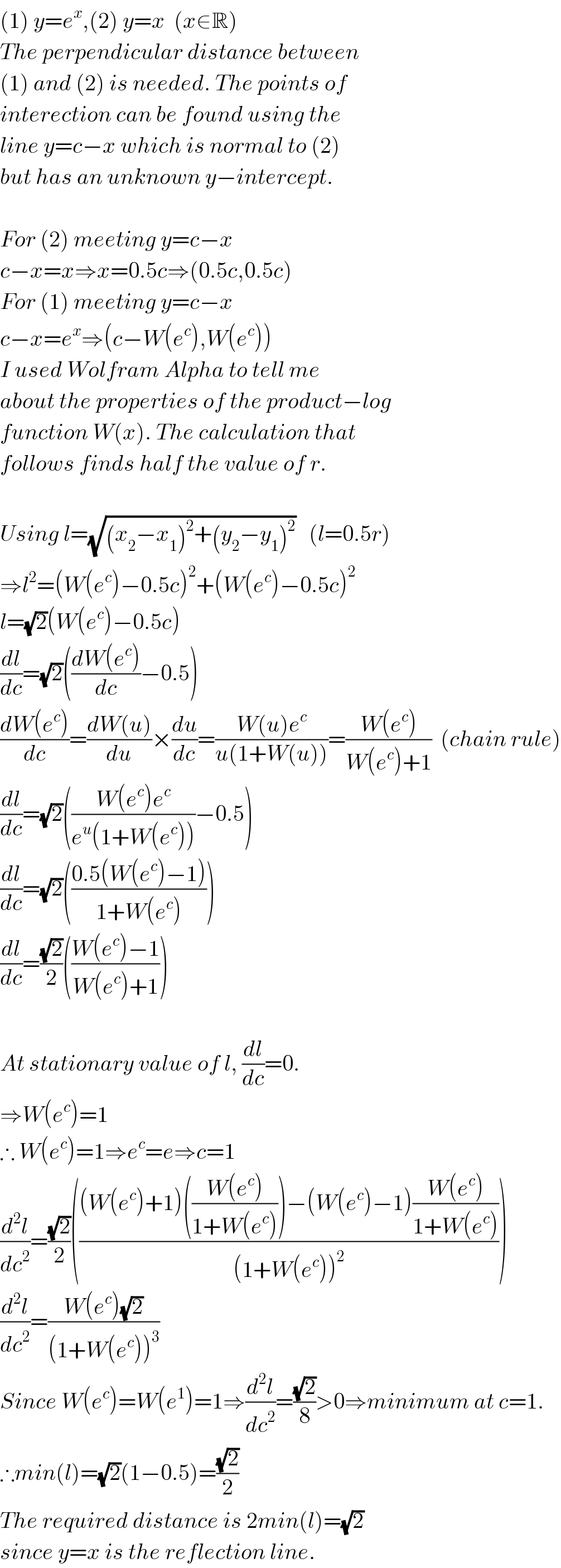
(1) y=e^x ,(2) y=x (x∈R) The perpendicular distance between (1) and (2) is needed. The points of interection can be found using the line y=c−x which is normal to (2) but has an unknown y−intercept. For (2) meeting y=c−x c−x=x⇒x=0.5c⇒(0.5c,0.5c) For (1) meeting y=c−x c−x=e^x ⇒(c−W(e^c ),W(e^c )) I used Wolfram Alpha to tell me about the properties of the product−log function W(x). The calculation that follows finds half the value of r. Using l=(√((x_2 −x_1 )^2 +(y_2 −y_1 )^2 )) (l=0.5r) ⇒l^2 =(W(e^c )−0.5c)^2 +(W(e^c )−0.5c)^2 l=(√2)(W(e^c )−0.5c) (dl/dc)=(√2)(((dW(e^c ))/dc)−0.5) ((dW(e^c ))/dc)=((dW(u))/du)×(du/dc)=((W(u)e^c )/(u(1+W(u))))=((W(e^c ))/(W(e^c )+1)) (chain rule) (dl/dc)=(√2)(((W(e^c )e^c )/(e^u (1+W(e^c ))))−0.5) (dl/dc)=(√2)(((0.5(W(e^c )−1))/(1+W(e^c )))) (dl/dc)=((√2)/2)(((W(e^c )−1)/(W(e^c )+1))) At stationary value of l, (dl/dc)=0. ⇒W(e^c )=1 ∴ W(e^c )=1⇒e^c =e⇒c=1 (d^2 l/dc^2 )=((√2)/2)((((W(e^c )+1)(((W(e^c ))/(1+W(e^c ))))−(W(e^c )−1)((W(e^c ))/(1+W(e^c ))))/((1+W(e^c ))^2 ))) (d^2 l/dc^2 )=((W(e^c )(√2))/((1+W(e^c ))^3 )) Since W(e^c )=W(e^1 )=1⇒(d^2 l/dc^2 )=((√2)/8)>0⇒minimum at c=1. ∴min(l)=(√2)(1−0.5)=((√2)/2) The required distance is 2min(l)=(√2) since y=x is the reflection line.

$$\left(\mathrm{1}\right)\:{y}={e}^{{x}} ,\left(\mathrm{2}\right)\:{y}={x}\:\:\left({x}\in\mathbb{R}\right) \\ $$$${The}\:{perpendicular}\:{distance}\:{between} \\ $$$$\left(\mathrm{1}\right)\:{and}\:\left(\mathrm{2}\right)\:{is}\:{needed}.\:{The}\:{points}\:{of} \\ $$$${interection}\:{can}\:{be}\:{found}\:{using}\:{the} \\ $$$${line}\:{y}={c}−{x}\:{which}\:{is}\:{normal}\:{to}\:\left(\mathrm{2}\right) \\ $$$${but}\:{has}\:{an}\:{unknown}\:{y}−{intercept}. \\ $$$$ \\ $$$${For}\:\left(\mathrm{2}\right)\:{meeting}\:{y}={c}−{x} \\ $$$${c}−{x}={x}\Rightarrow{x}=\mathrm{0}.\mathrm{5}{c}\Rightarrow\left(\mathrm{0}.\mathrm{5}{c},\mathrm{0}.\mathrm{5}{c}\right) \\ $$$${For}\:\left(\mathrm{1}\right)\:{meeting}\:{y}={c}−{x} \\ $$$${c}−{x}={e}^{{x}} \Rightarrow\left({c}−{W}\left({e}^{{c}} \right),{W}\left({e}^{{c}} \right)\right) \\ $$$${I}\:{used}\:{Wolfram}\:{Alpha}\:{to}\:{tell}\:{me} \\ $$$${about}\:{the}\:{properties}\:{of}\:{the}\:{product}−{log} \\ $$$${function}\:{W}\left({x}\right).\:{The}\:{calculation}\:{that} \\ $$$${follows}\:{finds}\:{half}\:{the}\:{value}\:{of}\:{r}. \\ $$$$ \\ $$$${Using}\:{l}=\sqrt{\left({x}_{\mathrm{2}} −{x}_{\mathrm{1}} \right)^{\mathrm{2}} +\left({y}_{\mathrm{2}} −{y}_{\mathrm{1}} \right)^{\mathrm{2}} }\:\:\:\left({l}=\mathrm{0}.\mathrm{5}{r}\right) \\ $$$$\Rightarrow{l}^{\mathrm{2}} =\left({W}\left({e}^{{c}} \right)−\mathrm{0}.\mathrm{5}{c}\right)^{\mathrm{2}} +\left({W}\left({e}^{{c}} \right)−\mathrm{0}.\mathrm{5}{c}\right)^{\mathrm{2}} \\ $$$${l}=\sqrt{\mathrm{2}}\left({W}\left({e}^{{c}} \right)−\mathrm{0}.\mathrm{5}{c}\right)\:\: \\ $$$$\frac{{dl}}{{dc}}=\sqrt{\mathrm{2}}\left(\frac{{dW}\left({e}^{{c}} \right)}{{dc}}−\mathrm{0}.\mathrm{5}\right) \\ $$$$\frac{{dW}\left({e}^{{c}} \right)}{{dc}}=\frac{{dW}\left({u}\right)}{{du}}×\frac{{du}}{{dc}}=\frac{{W}\left({u}\right){e}^{{c}} }{{u}\left(\mathrm{1}+{W}\left({u}\right)\right)}=\frac{{W}\left({e}^{{c}} \right)}{{W}\left({e}^{{c}} \right)+\mathrm{1}}\:\:\left({chain}\:{rule}\right) \\ $$$$\frac{{dl}}{{dc}}=\sqrt{\mathrm{2}}\left(\frac{{W}\left({e}^{{c}} \right){e}^{{c}} }{{e}^{{u}} \left(\mathrm{1}+{W}\left({e}^{{c}} \right)\right)}−\mathrm{0}.\mathrm{5}\right) \\ $$$$\frac{{dl}}{{dc}}=\sqrt{\mathrm{2}}\left(\frac{\mathrm{0}.\mathrm{5}\left({W}\left({e}^{{c}} \right)−\mathrm{1}\right)}{\mathrm{1}+{W}\left({e}^{{c}} \right)}\right) \\ $$$$\frac{{dl}}{{dc}}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\frac{{W}\left({e}^{{c}} \right)−\mathrm{1}}{{W}\left({e}^{{c}} \right)+\mathrm{1}}\right) \\ $$$$ \\ $$$${At}\:{stationary}\:{value}\:{of}\:{l},\:\frac{{dl}}{{dc}}=\mathrm{0}. \\ $$$$\Rightarrow{W}\left({e}^{{c}} \right)=\mathrm{1} \\ $$$$\therefore\:{W}\left({e}^{{c}} \right)=\mathrm{1}\Rightarrow{e}^{{c}} ={e}\Rightarrow{c}=\mathrm{1} \\ $$$$\frac{{d}^{\mathrm{2}} {l}}{{dc}^{\mathrm{2}} }=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\frac{\left({W}\left({e}^{{c}} \right)+\mathrm{1}\right)\left(\frac{{W}\left({e}^{{c}} \right)}{\mathrm{1}+{W}\left({e}^{{c}} \right)}\right)−\left({W}\left({e}^{{c}} \right)−\mathrm{1}\right)\frac{{W}\left({e}^{{c}} \right)}{\mathrm{1}+{W}\left({e}^{{c}} \right)}}{\left(\mathrm{1}+{W}\left({e}^{{c}} \right)\right)^{\mathrm{2}} }\right) \\ $$$$\frac{{d}^{\mathrm{2}} {l}}{{dc}^{\mathrm{2}} }=\frac{{W}\left({e}^{{c}} \right)\sqrt{\mathrm{2}}}{\left(\mathrm{1}+{W}\left({e}^{{c}} \right)\right)^{\mathrm{3}} } \\ $$$${Since}\:{W}\left({e}^{{c}} \right)={W}\left({e}^{\mathrm{1}} \right)=\mathrm{1}\Rightarrow\frac{{d}^{\mathrm{2}} {l}}{{dc}^{\mathrm{2}} }=\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}>\mathrm{0}\Rightarrow{minimum}\:{at}\:{c}=\mathrm{1}. \\ $$$$\therefore{min}\left({l}\right)=\sqrt{\mathrm{2}}\left(\mathrm{1}−\mathrm{0}.\mathrm{5}\right)=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$${The}\:{required}\:{distance}\:{is}\:\mathrm{2}{min}\left({l}\right)=\sqrt{\mathrm{2}} \\ $$$${since}\:{y}={x}\:{is}\:{the}\:{reflection}\:{line}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com