calculate ∫_(−∞) ^(+∞) ((x^2 −1)/((x^2 −x+3)^2 ))dx


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 56931 by turbo msup by abdo last updated on 26/Mar/19

$c a l c u l a t e \int_{- \infty}^{+ \infty} \frac{x^{2} - 1}{{(x^{2} - x + 3)}^{2}} d x$
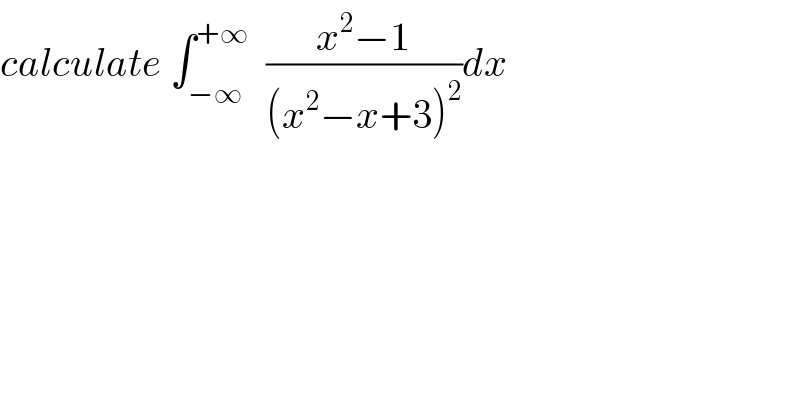
Commented by maxmathsup by imad last updated on 27/Mar/19
$residus method let ϕ(z) =((z^2 −1)/((z^2 −z +3)^2 )) let determine the poles of ϕ? z^2 −z+3=0 →Δ =1−12 =−11=(i(√(11)))^2 ⇒z_1 =((1+i(√(11)))/2) z_2 =((1−i(√(11)))/2) the poles of ϕ are z_1 and z_2 (doubles) and ϕ(z)=((z^2 −1)/((z−z_1 )^2 (z−z_2 )^2 )) residus theorem give ∫_(−∞) ^(+∞) ϕ(z)dz =2iπRes(ϕ,z_1 ) Res(ϕ,z_1 ) = lim_(z→z_1 ) (1/((2−1)!)) {(z−z_1 )^2 ϕ(z)}^((1)) =lim_(z→z_1 ) {((z^2 −1)/((z−z_2 )^2 ))}^((1)) =lim_(z→z_1 ) {((2z(z−z_2 )^2 −2(z−z_2 )(z^2 −1))/((z−z_2 )^4 ))} =lim_(z→z_1 ) ((2z(z−z_2 )−2(z^2 −1))/((z−z_2 )^3 )) =((2z_1 (z_1 −z_2 )−2(z_1 ^2 −1))/((z_1 −z_2 )^3 )) =((2i(√(11))(((1+i(√(11)))/2))−2( (1/4)(1+2i(√(11))−11)−1))/((i(√(11)))^3 )) =((i(√(11))(1+i(√(11)))−2{((i(√(11)))/2)−(5/2)−1})/(−11i(√(11)))) =((i(√(11))−11−i(√(11))+5 +2)/(−11i(√(11)))) =((−4)/(−11i(√(11)))) =(4/(11i(√(11)))) ⇒∫_(−∞) ^(+∞) ϕ(z)dz =2iπ (4/(11i(√(11)))) =((8π)/(11(√(11)))) =((8π(√(11)))/(121)) ★∫_(−∞) ^(+∞) ((x^2 −1)/((x^2 −x+3)^2 )) dx =((8π(√(11)))/(121)) ★$
$r e s i d u s m e t h o d l e t φ (z) = \frac{z^{2} - 1}{{(z^{2} - z + 3)}^{2}} l e t d e t e r m i n e t h e p o l e s o f φ ?$ $z^{2} - z + 3 = 0 \to Δ = 1 - 12 = - 11 = {(i \sqrt{11})}^{2} \Rightarrow z_{1} = \frac{1 + i \sqrt{11}}{2}$ $z_{2} = \frac{1 - i \sqrt{11}}{2} t h e p o l e s o f φ a r e z_{1} a n d z_{2} (d o u b l e s) a n d φ (z) = \frac{z^{2} - 1}{{(z - z_{1})}^{2} {(z - z_{2})}^{2}}$ $r e s i d u s t h e o r e m g i v e \int_{- \infty}^{+ \infty} φ (z) d z = 2 i π R e s (φ, z_{1})$ $R e s (φ, z_{1}) = {l i m}_{z \to z_{1}} \frac{1}{(2 - 1)!} {{(z - z_{1})}^{2} φ (z)}^{(1)}$ $= {l i m}_{z \to z_{1}} {\frac{z^{2} - 1}{{(z - z_{2})}^{2}}}^{(1)} = {l i m}_{z \to z_{1}} {\frac{2 z {(z - z_{2})}^{2} - 2 (z - z_{2}) (z^{2} - 1)}{{(z - z_{2})}^{4}}}$ $= {l i m}_{z \to z_{1}} \frac{2 z (z - z_{2}) - 2 (z^{2} - 1)}{{(z - z_{2})}^{3}} = \frac{2 z_{1} (z_{1} - z_{2}) - 2 (z_{1}^{2} - 1)}{{(z_{1} - z_{2})}^{3}}$ $= \frac{2 i \sqrt{11} (\frac{1 + i \sqrt{11}}{2}) - 2 (\frac{1}{4} (1 + 2 i \sqrt{11} - 11) - 1)}{{(i \sqrt{11})}^{3}}$ $= \frac{i \sqrt{11} (1 + i \sqrt{11}) - 2 {\frac{i \sqrt{11}}{2} - \frac{5}{2} - 1}}{- 11 i \sqrt{11}} = \frac{i \sqrt{11} - 11 - i \sqrt{11} + 5 + 2}{- 11 i \sqrt{11}}$ $= \frac{- 4}{- 11 i \sqrt{11}} = \frac{4}{11 i \sqrt{11}} \Rightarrow \int_{- \infty}^{+ \infty} φ (z) d z = 2 i π \frac{4}{11 i \sqrt{11}} = \frac{8 π}{11 \sqrt{11}} = \frac{8 π \sqrt{11}}{121}$ $★ \int_{- \infty}^{+ \infty} \frac{x^{2} - 1}{{(x^{2} - x + 3)}^{2}} d x = \frac{8 π \sqrt{11}}{121} ★$
	Answered by MJS last updated on 27/Mar/19

	${Ostrogradski}^{'} s Method once again$ $\int \frac{p (x)}{q (x)} d x = \frac{p_{1} (x)}{q_{1} (x)} + \int \frac{p_{2} (x)}{q_{2} (x)} d x$ $q_{1} (x) = \gcd (q (x), q^{'} (x))$ $q_{2} (x) = \frac{q (x)}{q_{1} (x)}$ $p_{1} (x), p_{2} (x) can be found like this :$ $\frac{p (x)}{q (x)} = \frac{d}{d x} [\frac{p_{1} (x)}{q_{1} (x)}] + \frac{p_{2} (x)}{q_{2} (x)}$ $in our case :$ $\int \frac{x^{2} - 1}{{(x^{2} - x + 3)}^{2}} d x = - \frac{7 x + 2}{11 (x^{2} - x + 3)} + \frac{4}{11} \int \frac{d x}{x^{2} - x + 3} =$ $= - \frac{7 x + 2}{11 (x^{2} - x + 3)} + \frac{8 \sqrt{11}}{121} \arctan (\frac{\sqrt{11}}{11} (2 x - 1)) + C$ $\underset{- \infty}{\int^{+ \infty}} \frac{x^{2} - 1}{{(x^{2} - x + 3)}^{2}} d x = \frac{8 \sqrt{11}}{121} π$
	Commented by turbo msup by abdo last updated on 27/Mar/19

	$t h a n k s s i r m j s .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum