
Question and Answers Forum
Question Number 57225 by maxmathsup by imad last updated on 31/Mar/19
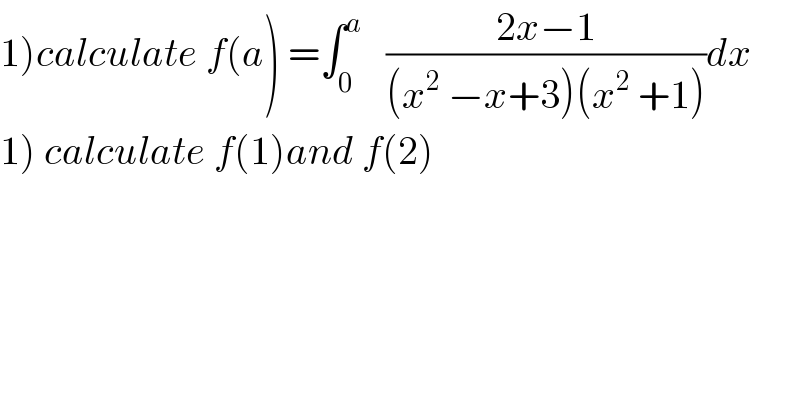
Commented by maxmathsup by imad last updated on 04/Apr/19
![let decompose F(x) =((2x−1)/((x^2 −x+3)(x^2 +1))) ⇒ F(x) =((ax+b)/(x^2 −x+3)) +((cx+d)/(x^2 +1)) ⇒(ax+b)(x^2 +1)+(cx+d)(x^2 −x+3) =2x−1 ⇒ ax^3 +ax +bx^2 +b +cx^3 −cx^2 +3cx +dx^2 −dx +3d =2x−1 ⇒ (a+c)x^3 +(b−c +d)x^2 +(a +3c−d)x +b +3d =2x−1 ⇒ a+c =0 and b−c+d =0 and a+3c−d =2 and 3d=−1 ⇒ d =−(1/3) c=−a ⇒a−3a −d =2 ⇒−2a =d+2 =−(1/3) +2 =(5/3) ⇒a =−(5/6) c =(5/6) ,b =c−d =(5/6) +(1/3) =(7/6) ⇒ F(x) =((−(5/6)x +(7/6))/(x^2 −x+3)) +(((5/6)x−(2/6))/(x^2 +1)) =−(1/6) ((x−7)/(x^2 −x+3)) +(1/6) ((5x−2)/(x^2 +1)) ⇒ ∫ F(x)dx =−(1/(12)) ∫ ((2x−14)/(x^2 −x +3))dx +(5/(12)) ∫ ((2x)/(x^2 +1)) −(1/3) ∫ (dx/(x^2 +1)) =−(1/(12))ln(x^2 −x +3) +((13)/(12)) ∫ (dx/(x^2 −x +3)) +(5/(12))ln(x^2 +1)−(1/3) arctan(x) +c but ∫ (dx/(x^2 −x+3)) =∫ (dx/(x^2 −2(x/2) +(1/4)+3−(1/4))) =∫ (dx/((x−(1/2))^2 +((11)/4))) =_(x−(1/2)=((√(11))/2)u) (4/(11))∫ (1/(1+u^2 )) ((√(11))/2) du =(2/(√(11))) arctan(((2x−1)/(√(11)))) ⇒ ∫ F(x)dx =−(1/(12))ln(x^2 −x+3) +((13)/(6(√(11)))) arctan(((2x−1)/(√(11)))) +(5/(12))ln(x^2 +1)−(1/3)arctan(x)+c ⇒f(a) =∫_0 ^a F(x)dx =[−(1/(12))ln(x^2 −x+3)+((13)/(6(√(11)))) arctan(((2x−1)/(√(11))))+(5/(12))ln(x^2 +1)−(1/3) arctan(x)]_0 ^a =−(1/(12))ln(a^2 −a +3)+((13)/(6(√(11)))) arctan(((2a−1)/(√(11))))+(5/(12))ln(a^2 +1)−(1/3) arctan(a) +(1/(12))ln(3) +((13)/(6(√(11)))) arctan((1/(√(11))))](Q57467.png)
Commented by maxmathsup by imad last updated on 05/Apr/19
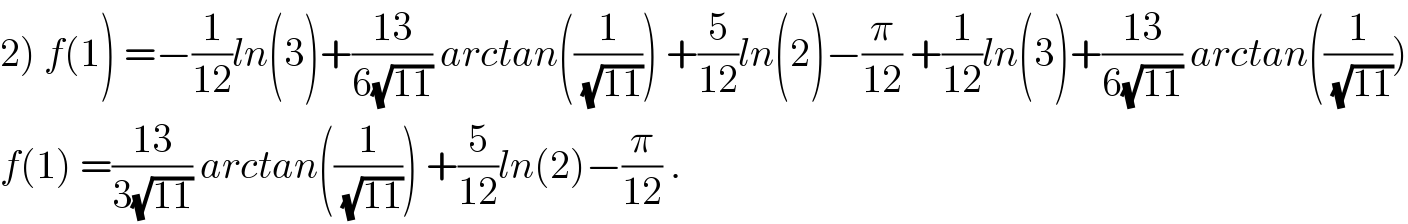
| ||
Question and Answers Forum | ||
Question Number 57225 by maxmathsup by imad last updated on 31/Mar/19 | ||
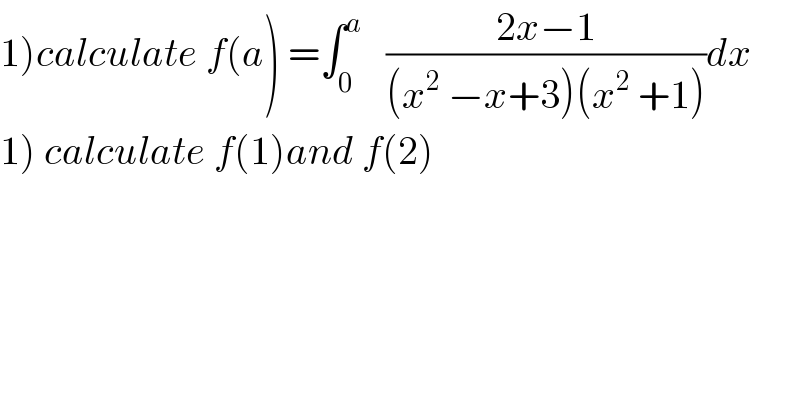 | ||
Commented by maxmathsup by imad last updated on 04/Apr/19 | ||
![let decompose F(x) =((2x−1)/((x^2 −x+3)(x^2 +1))) ⇒ F(x) =((ax+b)/(x^2 −x+3)) +((cx+d)/(x^2 +1)) ⇒(ax+b)(x^2 +1)+(cx+d)(x^2 −x+3) =2x−1 ⇒ ax^3 +ax +bx^2 +b +cx^3 −cx^2 +3cx +dx^2 −dx +3d =2x−1 ⇒ (a+c)x^3 +(b−c +d)x^2 +(a +3c−d)x +b +3d =2x−1 ⇒ a+c =0 and b−c+d =0 and a+3c−d =2 and 3d=−1 ⇒ d =−(1/3) c=−a ⇒a−3a −d =2 ⇒−2a =d+2 =−(1/3) +2 =(5/3) ⇒a =−(5/6) c =(5/6) ,b =c−d =(5/6) +(1/3) =(7/6) ⇒ F(x) =((−(5/6)x +(7/6))/(x^2 −x+3)) +(((5/6)x−(2/6))/(x^2 +1)) =−(1/6) ((x−7)/(x^2 −x+3)) +(1/6) ((5x−2)/(x^2 +1)) ⇒ ∫ F(x)dx =−(1/(12)) ∫ ((2x−14)/(x^2 −x +3))dx +(5/(12)) ∫ ((2x)/(x^2 +1)) −(1/3) ∫ (dx/(x^2 +1)) =−(1/(12))ln(x^2 −x +3) +((13)/(12)) ∫ (dx/(x^2 −x +3)) +(5/(12))ln(x^2 +1)−(1/3) arctan(x) +c but ∫ (dx/(x^2 −x+3)) =∫ (dx/(x^2 −2(x/2) +(1/4)+3−(1/4))) =∫ (dx/((x−(1/2))^2 +((11)/4))) =_(x−(1/2)=((√(11))/2)u) (4/(11))∫ (1/(1+u^2 )) ((√(11))/2) du =(2/(√(11))) arctan(((2x−1)/(√(11)))) ⇒ ∫ F(x)dx =−(1/(12))ln(x^2 −x+3) +((13)/(6(√(11)))) arctan(((2x−1)/(√(11)))) +(5/(12))ln(x^2 +1)−(1/3)arctan(x)+c ⇒f(a) =∫_0 ^a F(x)dx =[−(1/(12))ln(x^2 −x+3)+((13)/(6(√(11)))) arctan(((2x−1)/(√(11))))+(5/(12))ln(x^2 +1)−(1/3) arctan(x)]_0 ^a =−(1/(12))ln(a^2 −a +3)+((13)/(6(√(11)))) arctan(((2a−1)/(√(11))))+(5/(12))ln(a^2 +1)−(1/3) arctan(a) +(1/(12))ln(3) +((13)/(6(√(11)))) arctan((1/(√(11))))](Q57467.png) | ||
Commented by maxmathsup by imad last updated on 05/Apr/19 | ||
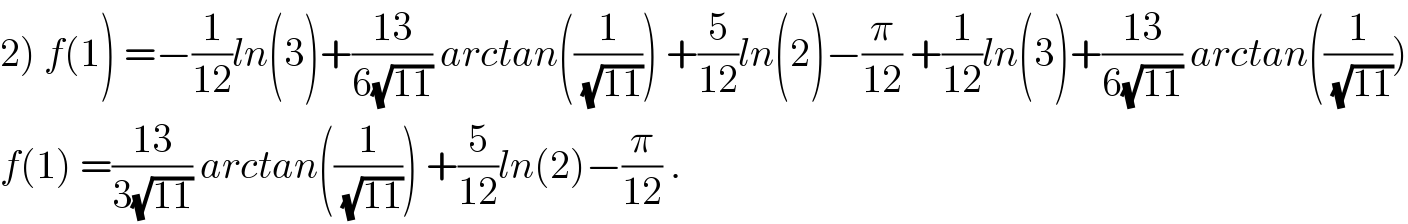 | ||