Question Number 57236 by maxmathsup by imad last updated on 31/Mar/19
$${clalculate}\:{A}_{{n}} =\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{\mathrm{2}{n}} \left(\mathrm{1}−{t}\right)^{{n}} {dt}\:\:\:{with}\:{n}\:{integr}\:{natural}\:. \\ $$
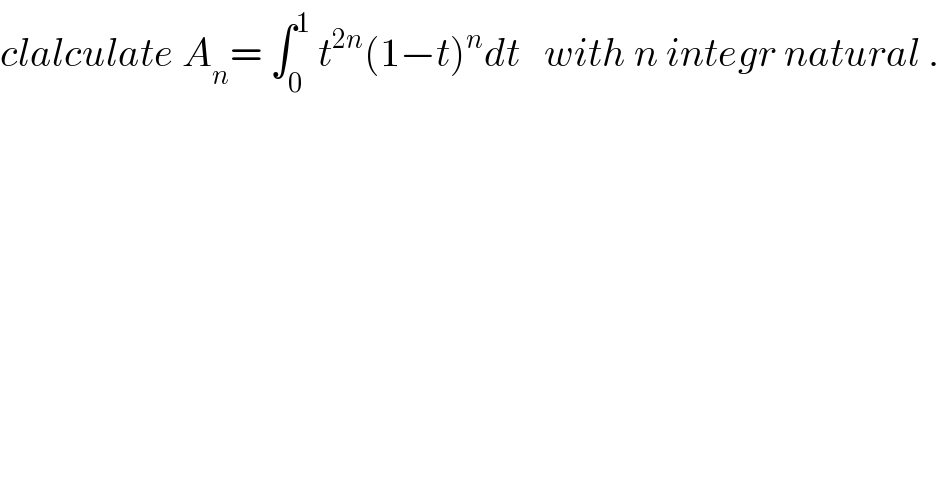
Commented by maxmathsup by imad last updated on 04/Apr/19
![let find A_(n,p) =∫_0 ^1 t^n (1−t)^p dt by parts u^′ =t^n and v=(1−t)^p A_(n,p) =[(1/(n+1))t^(n+1) (1−t)^p ]_0 ^1 −∫_0 ^1 (1/(n+1))t^(n+1) (−p)(1−t)^(p−1) dt =(p/(n+1)) ∫_0 ^1 t^(n+1) (1−t)^(p−1) =(p/(n+1)) A_(n+1,p−1) ⇒ A_(n,p) =((p(p−1))/((n+1)(n+2))) A_(n+2,p−2) =((p(p−1)...(p−k+1))/((n+1)(n+2)....(n+k)))A_(n+k,p−k) .=_(k=p) ((p!)/((n+1)(n+2)....(n+p)))A_(n+p,o) A_(n+p,0) =∫_0 ^1 t^(n+p) dt =(1/(n+p+1)) ⇒A_(n,p) =((p!)/((n+1)(n+2)...(n+p+1))) ⇒ A_(n,p) =((p!)/((n+p+1)!)) ×n! =((n! .p!)/((n+p+1)!)) ⇒ A_n =A_(2n,n) =(((2n)!(n!))/((3n+1)!))](Q57449.png)
$${let}\:{find}\:{A}_{{n},{p}} \:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{{n}} \left(\mathrm{1}−{t}\right)^{{p}} {dt}\:\:{by}\:{parts}\:{u}^{'} ={t}^{{n}} \:{and}\:{v}=\left(\mathrm{1}−{t}\right)^{{p}} \\ $$$${A}_{{n},{p}} \:=\left[\frac{\mathrm{1}}{{n}+\mathrm{1}}{t}^{{n}+\mathrm{1}} \left(\mathrm{1}−{t}\right)^{{p}} \right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}}{{n}+\mathrm{1}}{t}^{{n}+\mathrm{1}} \:\left(−{p}\right)\left(\mathrm{1}−{t}\right)^{{p}−\mathrm{1}} {dt} \\ $$$$=\frac{{p}}{{n}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{{n}+\mathrm{1}} \left(\mathrm{1}−{t}\right)^{{p}−\mathrm{1}} \:=\frac{{p}}{{n}+\mathrm{1}}\:{A}_{{n}+\mathrm{1},{p}−\mathrm{1}} \:\Rightarrow \\ $$$${A}_{{n},{p}} =\frac{{p}\left({p}−\mathrm{1}\right)}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}\:{A}_{{n}+\mathrm{2},{p}−\mathrm{2}} =\frac{{p}\left({p}−\mathrm{1}\right)...\left({p}−{k}+\mathrm{1}\right)}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)....\left({n}+{k}\right)}{A}_{{n}+{k},{p}−{k}} .=_{{k}={p}} \frac{{p}!}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)....\left({n}+{p}\right)}{A}_{{n}+{p},{o}} \\ $$$${A}_{{n}+{p},\mathrm{0}} =\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{n}+{p}} {dt}\:=\frac{\mathrm{1}}{{n}+{p}+\mathrm{1}}\:\Rightarrow{A}_{{n},{p}} \:=\frac{{p}!}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)...\left({n}+{p}+\mathrm{1}\right)}\:\Rightarrow \\ $$$${A}_{{n},{p}} =\frac{{p}!}{\left({n}+{p}+\mathrm{1}\right)!}\:×{n}!\:=\frac{{n}!\:.{p}!}{\left({n}+{p}+\mathrm{1}\right)!}\:\Rightarrow\:{A}_{{n}} ={A}_{\mathrm{2}{n},{n}} \:=\frac{\left(\mathrm{2}{n}\right)!\left({n}!\right)}{\left(\mathrm{3}{n}+\mathrm{1}\right)!} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 01/Apr/19
$$\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\mathrm{2}{n}+\mathrm{1}−\mathrm{1}} \left(\mathrm{1}−{t}\right)^{{n}+\mathrm{1}−\mathrm{1}} =\frac{\lceil\left(\mathrm{2}{n}+\mathrm{1}\right)\lceil\left({n}+\mathrm{1}\right)}{\lceil\left(\mathrm{2}{n}+\mathrm{1}+{n}+\mathrm{1}\right)} \\ $$$${beta}\:{function}\:\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{m}−\mathrm{1}} \left(\mathrm{1}−{x}\right)^{{n}−\mathrm{1}} {dx}=\frac{\left.\lceil\left({m}\right)\lceil{n}\right)}{\lceil\left({m}+{n}\right)} \\ $$
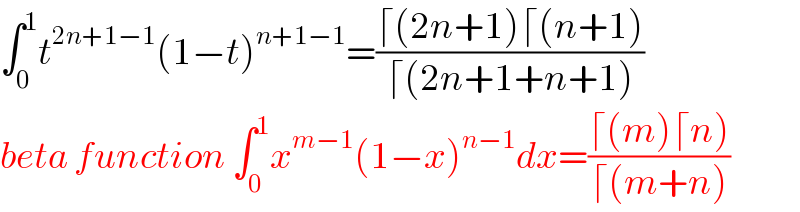
Commented by maxmathsup by imad last updated on 04/Apr/19
$${sir}\:{Tanmay}\:{look}\:{that}\:\Gamma\left(\mathrm{2}{n}+\mathrm{1}\right)=\left(\mathrm{2}{n}\right)!\:\:\:,\Gamma\left({n}+\mathrm{1}\right)={n}!\:,\Gamma\left(\mathrm{3}{n}+\mathrm{2}\right)=\left(\mathrm{3}{n}+\mathrm{1}\right)! \\ $$$$\Rightarrow{A}_{{n}} =\frac{\left(\mathrm{2}{n}\right)!\left({n}!\right)}{\left(\mathrm{3}{n}+\mathrm{1}\right)!}\:\:. \\ $$