
Question and Answers Forum
Question Number 57319 by turbo msup by abdo last updated on 02/Apr/19
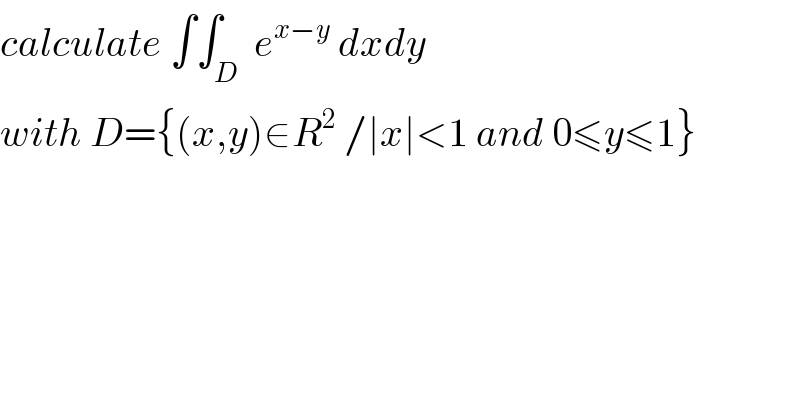
Commented bymaxmathsup by imad last updated on 02/Apr/19
![let I =∫∫_D e^(x−y) dxdy ⇒I =∫_(−1) ^1 e^x dx .∫_0 ^1 e^(−y) dy =[e^x ]_(−1) ^1 .[−e^(−y) ]_0 ^1 =(e−e^(−1) )(1−e^(−1) ) =e−1−e^(−1) +e^(−2) ⇒I =e−1−(1/e) +(1/e^2 ) .](Q57342.png)
Answered by kaivan.ahmadi last updated on 02/Apr/19
![∫_0 ^1 ∫_(−1) ^1 e^(x−y) dxdy=∫_0 ^1 e^(x−y) ∣_(−1) ^1 dy= ∫_0 ^1 (e^(1−y) −e^(−1−y) )dy= −e^(1−y) +e^(−1−y) ∣_0 ^1 =[−1+e^(−2) ]−[−e+e^(−1) ]= −1+(1/e^2 )+e−(1/e)=((−e^2 +1+e^3 −e)/e^2 )](Q57322.png)
| ||
Question and Answers Forum | ||
Question Number 57319 by turbo msup by abdo last updated on 02/Apr/19 | ||
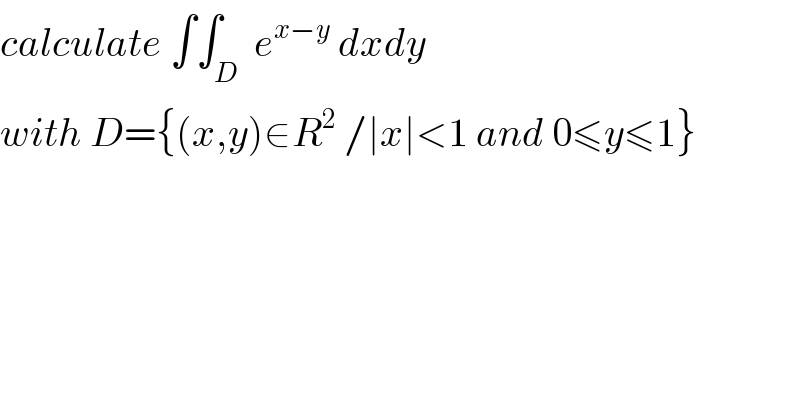 | ||
Commented bymaxmathsup by imad last updated on 02/Apr/19 | ||
![let I =∫∫_D e^(x−y) dxdy ⇒I =∫_(−1) ^1 e^x dx .∫_0 ^1 e^(−y) dy =[e^x ]_(−1) ^1 .[−e^(−y) ]_0 ^1 =(e−e^(−1) )(1−e^(−1) ) =e−1−e^(−1) +e^(−2) ⇒I =e−1−(1/e) +(1/e^2 ) .](Q57342.png) | ||
Answered by kaivan.ahmadi last updated on 02/Apr/19 | ||
![∫_0 ^1 ∫_(−1) ^1 e^(x−y) dxdy=∫_0 ^1 e^(x−y) ∣_(−1) ^1 dy= ∫_0 ^1 (e^(1−y) −e^(−1−y) )dy= −e^(1−y) +e^(−1−y) ∣_0 ^1 =[−1+e^(−2) ]−[−e+e^(−1) ]= −1+(1/e^2 )+e−(1/e)=((−e^2 +1+e^3 −e)/e^2 )](Q57322.png) | ||
| ||