
Question and Answers Forum
Question Number 57323 by turbo msup by abdo last updated on 02/Apr/19
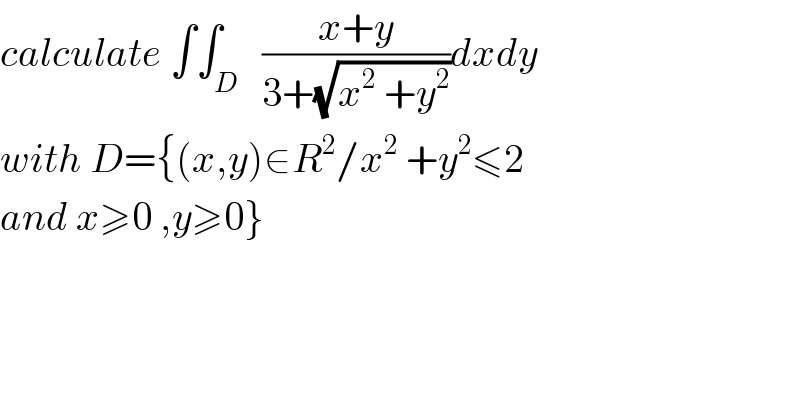
Commented by maxmathsup by imad last updated on 03/Apr/19
![let use the diffeomorphism x=rcosθ and y=rsinθ we have x^2 +y^2 ≤2 ⇒ r^2 ≤2 ⇒0≤r≤(√2) also x≥0 and y ≥0 ⇒0≤θ ≤(π/2) ⇒ ∫∫_D ((x+y)/(3+(√(x^2 +y^2 ))))dxdy =∫∫_(0≤r≤(√2) and 0≤θ≤(π/2)) ((r(cosθ +sinθ))/(3+r)) rdrdθ =∫_0 ^(√2) (r^2 /(3+r))dr .∫_0 ^(π/2) (cosθ +sinθ)dθ but ∫_0 ^(√2) (r^2 /(r+3)) dr =∫_0 ^(√2) ((r^2 −9 +9)/(r+3))dr =∫_0 ^(√2) (r−3)dr +9 ∫_1 ^(√2) (dr/(r+3)) =[(r^2 /2)−3r]_0 ^(√2) +9[ln∣r+3∣]_1 ^(√2) =1−3(√2) +9{ ln(3+(√2))−2ln(2)} =1−3ln(2)+9ln(3+(√2))−18ln(2) =1+9ln(3+(√2))−21ln(2) ∫_0 ^(π/2) (cosθ +sinθ)dθ =[sinθ −cosθ]_0 ^(π/2) =1−(−1) =2 ⇒ ∫∫_D ((x+y)/(3+(√(x^2 +y^2 ))))dxdy =2 +18ln(3+(√2))−42ln(2).](Q57346.png)
| ||
Question and Answers Forum | ||
Question Number 57323 by turbo msup by abdo last updated on 02/Apr/19 | ||
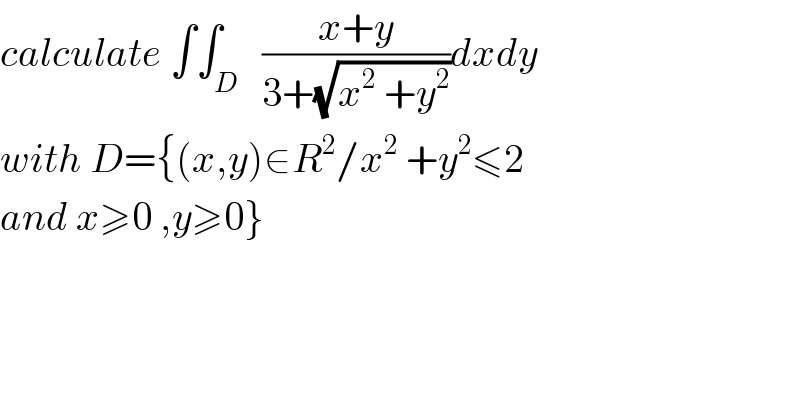 | ||
Commented by maxmathsup by imad last updated on 03/Apr/19 | ||
![let use the diffeomorphism x=rcosθ and y=rsinθ we have x^2 +y^2 ≤2 ⇒ r^2 ≤2 ⇒0≤r≤(√2) also x≥0 and y ≥0 ⇒0≤θ ≤(π/2) ⇒ ∫∫_D ((x+y)/(3+(√(x^2 +y^2 ))))dxdy =∫∫_(0≤r≤(√2) and 0≤θ≤(π/2)) ((r(cosθ +sinθ))/(3+r)) rdrdθ =∫_0 ^(√2) (r^2 /(3+r))dr .∫_0 ^(π/2) (cosθ +sinθ)dθ but ∫_0 ^(√2) (r^2 /(r+3)) dr =∫_0 ^(√2) ((r^2 −9 +9)/(r+3))dr =∫_0 ^(√2) (r−3)dr +9 ∫_1 ^(√2) (dr/(r+3)) =[(r^2 /2)−3r]_0 ^(√2) +9[ln∣r+3∣]_1 ^(√2) =1−3(√2) +9{ ln(3+(√2))−2ln(2)} =1−3ln(2)+9ln(3+(√2))−18ln(2) =1+9ln(3+(√2))−21ln(2) ∫_0 ^(π/2) (cosθ +sinθ)dθ =[sinθ −cosθ]_0 ^(π/2) =1−(−1) =2 ⇒ ∫∫_D ((x+y)/(3+(√(x^2 +y^2 ))))dxdy =2 +18ln(3+(√2))−42ln(2).](Q57346.png) | ||